Оглавление:



Коэффициент корреляции
- Коэффициент корреляции Эта глава посвящена ковариации. Это Это очень удобно с математической точки зрения, Ковариация является особенно хорошим показателем отношений Ранг. Раздел 1.9 рассматривает недостаток. Более точное измерение Хави Коэффициент корреляции тесно связан с этим.
- Как дисперсия и ковариация, коэффициент корреляции имеет два Форма теоретическая и выборочная. Теоретический коэффициент корреляции Tz традиционно представлен греческой буквой p и произносится следующим образом: «Ро» соответствует латинскому «г». Этот фактор для переменных х и у Это определяется следующим образом: 47 pop.cov (x ,, y) ox, y Xyy ^ Por. \ 2 и (х) пор. \ Am (y) ^ c2 ^ (1 2 3) Ковариации.
Если хна независима, теоретическое значение равно нулю, поэтому p равно нулю. Людмила Фирмаль
Если есть положительная связь между переменными, после этого Ху и, следовательно, Ру — положительные. Строгий случай Для положительного линейного отношения р принимает максимальное значение, Равно 1 Точно так же он включается из-за отрицательной зависимости rhu. Минимальное значение равно 1 отрицательному.
Коэффициент корреляции выборки g является теоретическим Дисперсия и ковариация уравнения (1.23) с несмещенной оценкой Я забочусь Было показано, что такую оценку можно получить, умножив выбор Скальная дисперсия и ковариация нал / (I -1). так Ков (х, у) g- _ / l_jr 1 X ‘Y / * v / h * v / / O’ 2 4) J r Var (x) r Var (>>) V A Z-1 / I-I Коэффициент p / (n-1) уменьшается и поэтому избирателен корреляция r Cov (x, y) ХЧУ ВВар (х) Вар (у) * О ‘2 5)
- Как и p, максимальное значение r равно 1, Получается в строго линейных положительных отношениях. Выборочные значения хны (все точки на диаграмме рассеяния Следуйте точной восходящей прямой линии). Точно так же Если есть линейный отрицательный, принять минимальное значение -1 Зависимость (точки находятся точно на прямой, направленной вниз). r = значение O Указывает на отсутствие связи между наблюдениями в выборке. эм.
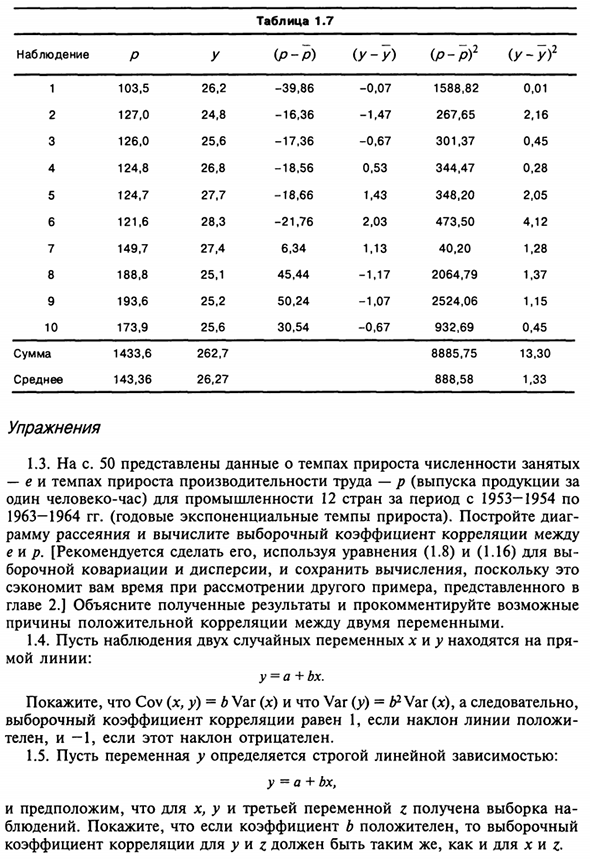
Конечно, тот факт, что r = 0, не обязательно означает p = 0. Менеджер по продажам. иллюстрации Чтобы объяснить расчет выборочного коэффициента корреляции, Используйте пример спроса на бензин в разделе 1.1. Данные Tab. 1.1 и показано на рисунке. 1.1. Cov (p, y) уже был рассчитан (см. Таблицу 1.2). Так как это -16.24, вам нужны только Var (p) и Var (y) (См. Таблицу 1.7).
Последние два столбца таблицы. 1,7 вар (р) 888,58 и Var (у) 1,33. Людмила Фирмаль
Так -16,24 -16,24 г = = = -0,47. / 1 9 £ \ / 888,58 x 1,33 34,38 u-z o; 48 Таблица 1.7 наблюдение 1 2 3 4 5 6 7 8 9 10 Сумма денег средняя P 103,5 127,0 126,0 124,8 124,7 121,6 149,7 188,8 193,6 173,9 1433,6 143,36 в 26,2 24,8 25,6 26,8 27,7 28,3 27,4 25,1 25,2 25,6 262,7 26,27 (PP) -39,86 -16,36 -17,36 -18,56 -18,66 -21,76 6,34 45,44 50,24 30,54 (U-U) -0,07 -1,47 -0,67 0,53 1,43 2,03 1,13 -1,17 -1,07 -0,67 (П-П) 2 1,588.82 267,65 301,37 344,47 348,20 473,50 40, 20 2,064.79 2,524.06 932,69 8,885.75 888,58 (Оо) 2 0,01 2,16 0,45 0,28 2,05 4,12 1,28 1,37 1,15 0,45 13,30 1,33 упражнения 1.3. р.
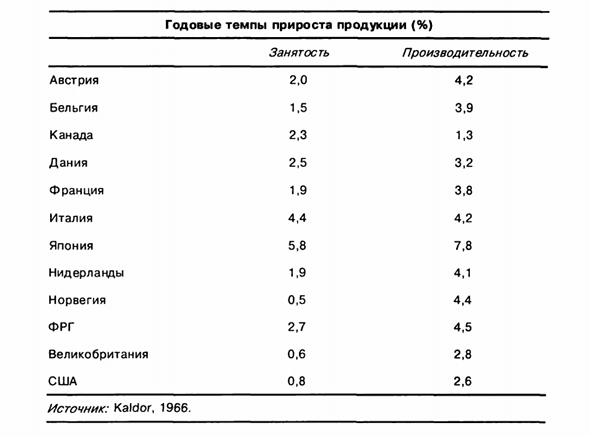
Показывает данные о росте сотрудников Скорость роста ее производительности труда Для отраслей в 12 странах с 1953 по 1954 год 1963-1964 годы (годовой темп роста индекса). Постройте диагноз Рассчитать выборочный коэффициент корреляции между кадрами рассеяния е и р. [Рекомендуется использовать формулы (1.8) и (1.16) Горизонтальная ковариация и дисперсия.
Экономьте время, рассматривая другой пример, показанный в Глава 2 Объясните результаты и прокомментируйте возможности Причина положительной корреляции между двумя переменными. 1.4. Предположим, что наблюдения двух случайных величин x и y находятся на прямой Моя линия: у = а + бх. Чтобы указать, что Cov (x, y) = b Var (x) и Var (y) = b1 Var (JC)
Если установлен наклон линии, коэффициент корреляции выборки равен 1 Тело. -1, если этот наклон отрицателен. 1,5. Предположим, что переменная y определяется строго линейным соотношением. у = а + бх, И образец х, у и третьей переменной г Наблюдение. Пример положительного коэффициента b.
Коэффициент корреляции между y и z должен быть таким же, как коэффициент корреляции между x и z. 49 Годовой темп роста производства (%) Занятый продуктивный Австрия Бельгия Канада Дания Франция Италия Япония Нидерланды Норвегия Германия Великобритания Америка Источник: Кардор, 1966. 2,0 1,5 2, 3 2.5 1,9 4,4 5,8 1,9 0,5 2,7 0.6 0.8 4,2 3,9 1,3 3,2 3,8 4,2 7,8 4,1 4,4 4, 5 2,8 2,6
Смотрите также:
| Правила расчета дисперсии | Почему ковариация не является хорошей мерой связи |
| Теоретическая дисперсия выборочного среднего | Коэффициент частной корреляции |

