Оглавление:


Деформированное состояние в точке. Линейные деформации. Деформации сдвига. Главные деформации
- Деформированное состояние в точке. Линейная деформация. Сдвиговые деформации. Основные изменения В общем случае
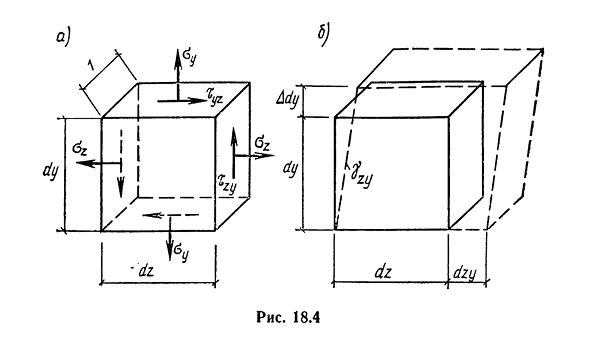
плоского напряженного состояния заданный бесконечно малый параллелепипед dyX x dzX l совпадает с нормальным напряжением, Oh, oz и Tzy, xyz(рис. 18.4, а).
Возникновение этих напряжений Людмила Фирмаль
сопровождается деформацией элемента: прямым удлинением его плоскости вдоль оси Oz, oh, укорочением вдоль оси Oh, изменением угла между его плоскостью dy и dz (деформацией сдвига). Покажем
линейное расширение элемента вдоль оси Oz\dz, вдоль оси OU kdy и вдоль оси Ox\dx. Деформация сдвига, характеризующая изменение угла между плоскостями dy и dz, обозначается углом сдвига yzy(рис. 18.4, б). В общем случае абсолютное удлинение граней M, y и Adz
- заменяется соответствующей продольной деформацией по формуле: Подопечные= \ dyldy и E2=\d2ldz. По аналогии с напряженным состоянием в точке вращения параллелепипеда d y z — \для различных углов и рассматриваемых точек продольной деформации и Y,
совокупность этих изменений для всех возможных положений грани характеризует деформированное состояние в этой точке. Понятно, что при определенном значении угла поворота параллелепипеда вблизи рассматриваемой точки a=A0 угол сдвига yzy будет равен нулю, то есть он будет ориентирован таким образом.
В теории упругости доказано, что основное нормальное напряжение и основная Людмила Фирмаль
деформация совпадают и действуют на основной участок. При фактическом расчете при любом значении Oy, uz и TSU сначала определяют местоположение основного участка, затем вычисляют основные нормальные напряжения o1t1ah и Otsh, а затем основные деформации Stakh и et1p.
Смотрите также:
Решение задач по технической механике

