Оглавление:
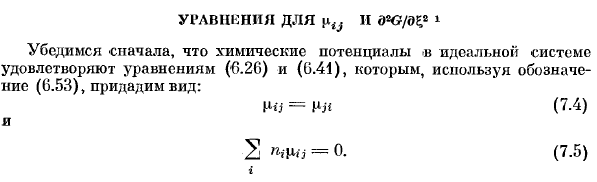




Уравнение для рц II
- Формула 1 Во-первых, мы проверяем, что химический потенциал идеальной системы удовлетворяет уравнениям (6.26) и (0.41). он использует обозначение (6.53) и дает следующий вид: И * = Mjf (7.4) И (7.5) 2 ПМЗ = { Из (7.1) молярная доля определяется следующим образом ч=»?(Т, п)+ Птин (7-6) V и,+ W2 +. 。 。 + ПС / в случае I f jf、 М _ _ рублей _ _ _ _ _ = _ золото + + ■ • • • + П. П Если t = /、 1 1.
В соответствии с (7.7), если μ\ 1 не совпадает, не зависит от индекса I. Таким образом, равенство (7.4) доказывается.
Поэтому появление производных достаточно просто. Людмила Фирмаль
- Чтобы вычислить сумму, напишите СЕ в форме: 」 2 ’Wj =» 1 + 2 (7-9) сумма, кроме i i i, распространяется на все значения y. From (7.8) и (7.7) следуют «1ч = М ’(Л-ий(7.10) л. v -, («>Id-ПТ ^ II) r t » / IL Фау-2 = — — — (/я-/?。.) =- Р7′/ 1 — Ж.(7.11) З \ это/ ■ J
Я Когда эти выражения подставляются в (7.9), происходит следующее: =(7.12) что это? Таким образом, это доказывает(7.5). Идеальная система всегда для (7.7)и (7.8) Число<0(1p /)(7.13) ЧКХ>0.(7.14)) Значение этих неравенств будет рассмотрено позже (см. Главу 15).
Функция идеальной системы, используя оптимальное значение добротности? C / можно рассчитать (см. главу VI,§ 5). Когда {7.7) присваивается (6.50)、 Р т в ПТ в в fXi В. Г Л чч = АРСС»^ — — -). (/. является)
Показатель dl2 2л \ Привет П; / П. Дж. И: (G. G2) продолжает = Ф *-п-п — ^ я(7.17) Д ^ Г 2л в РИИ Яц Дж \Щrij Ф В идеальной системе 043 ″ д-д-2gid. W> 0 и — > 0. (7.15) Использование базового алгебраического преобразования, которое трудно обрабатывать、
ffZQld£2£111 0 (7.19) ^»Статье 8J, dgpdb, — АГП-АИП Эти неравенства важны для изучения устойчивости термодинамических систем.
Если система поддерживает одновременное Р-индуцированных реакций Людмила Фирмаль
Смотрите также:
| Многофазные системы | Парциальные мольные величины |
| Идеальные системы и системы сравнения. Определение идеальных систем. | Сродство и однофазной идеальной системе |

