Оглавление:






Выбор параметров н синтез корректирующих устройств ио корневым годографам
- Выбор параметров и синтез устройства коррекции корневого годографа Видимость и простота исследования влияния отдельных параметров системы на их динамические свойства является несомненным преимуществом метода корневого годографа, который используется как для выбора параметров, так и для синтеза модифицированных устройств. Параметр a (коэффициент передачи элемента, постоянная времени, коэффициент демпфирования) должен быть выбран. Затем с постоянными значениями всех других параметров установите другие значения ai, a2, … в пределах возможных пределов изменения этого параметра в указанной системе и постройте траекторию маршрута (корневой годограф)
Это необходимо. Затем вы можете выбрать значение, где происходит наиболее выгодное расположение нулей и полюсов. Поскольку оценки качества корней близки и не требуют высокой точности, вычисления корней должны выполняться с использованием простейшего численного метода. Чтобы выбрать значение для коэффициента передачи k для системы с разомкнутым контуром, необходимо создать корневой годограф с k вариациями. Метод построения такого корневого годграфа был разработан очень подробно (см. П. 4.6).
Различные исходные позиции используются при синтезе корректирующего устройства. Людмила Фирмаль
В простейшем случае процесс перехода, как полагают, зависит от материального полюса, ближайшего к мнимой оси. В то же время мы используем предположение, что система обладает наилучшими динамическими свойствами, когда комплексная пара полюсных сопряжений находится ближе всего к мнимой оси. Однако добавление третьего полюса материала, который находится ближе всего к воображаемой оси, обычно улучшает качество переходного процесса. Также необходимо учитывать нулевой эффект передаточной функции. Поэтому для определения качества переходного процесса лучше всего рассмотреть три ближайших полюса и один ноль передаточной функции замкнутой системы.
Порядок композиции также может быть другим. Предположим, вам нужно выбрать устройство последовательной коррекции для конкретного показателя качества переходных характеристик и конкретного значения коэффициента передачи открытой системы k. Затем вы можете сделать следующее [1]: Изучить влияние k на показатель качества. Создайте корневой годограф нескорректированной системы при изменении k и найдите точку, соответствующую указанному показателю качества. Путем введения дополнительных нулей и полюсов прохождение траектории маршрута достигается с определенным значением k вблизи выбранной точки.
- Построить передаточную функцию последовательного корректора для дополнительных входных нулей и полюсов. Имейте в виду, что, хотя диполи, то есть полюсы и нули, находятся близко друг к другу, показатель качества вряд ли изменится, но передаточное число может быть увеличено. Пример расчета по приведенной выше схеме приведен в (1). Предположим, что динамика системы определяется парой комплексных сопряженных полюсов. Vo2 = -a0 ± / co0 (5,38) Далее передаточная функция замкнутой системы (5,39) Wj, (s) = кг / (Tls2 + 270 £ 0s — {- 1). На основании переходного отклика, соответствующего этой передаточной функции, зависимость a0 и co0 от времени управления / P и относительного перерегулирования <x [31, т.е. a0 «3 // p; o = e-pvv / sv. (5,40) Здесь состав последовательного корректора для заданного значения k, tP и a состоит из следующих этапов: …
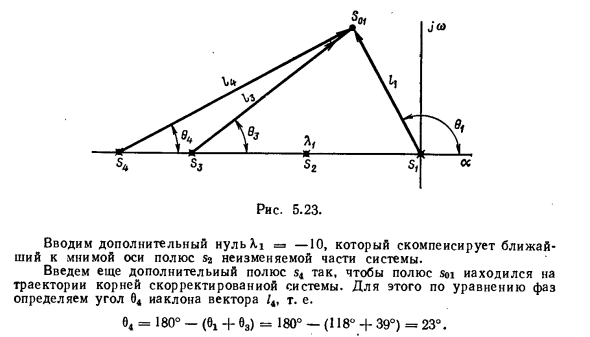
Введите дополнительный ноль A.i => –10. Это исправляет полюс s2 неизмененной части системы, ближайшей к мнимой оси. Введите дополнительный полюс s4 так, чтобы полюс soi находился в корневом местоположении настроенной системы. Для этого определяют угол 04 градиента вектора / 4 согласно фазовому уравнению. 04 = 180 ° — (0! -B b3) = 180 ° — (118 ° -} — 39 °) = 23 °
Вычисляет значение коэффициента передачи k, соответствующего корневой точке локуса сои настроенной системы k = /, 3/4 / (53 * 4) = 12,6 • 17,8 28,5 / (20 • 26,4) = 12. Людмила Фирмаль
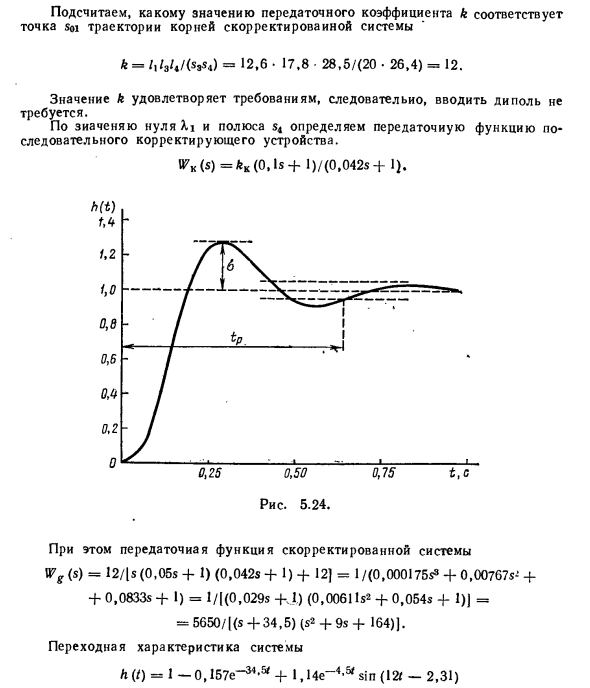
Значение k соответствует требованию, поэтому диполь не требуется. Определить передаточную функцию устройства последовательной коррекции на основе нуля Xi и полюса s4. U7k (S) = * K (0,1 с + 1) / (0,042 с + I). В этом случае передаточная функция настроенной системы равна Wg (s) = 12 / [s (0,05 с + 0 (0,042 с + 1) + 12) = 1 / (0,000175 с3 + 0,00707 с — + 0,0833 с -f I) = 1 / | (0,029 с -h) (0,0061 Is * 4-0,054 с 4-1) J = = 5G50 / | (s -f-34,5) (с2 4-9 с + 164 ) 1. Системный переходный ответ h (/) = l-0,157е ~~ Э4,5 ‘-f-1,14е4 «5 # sin (I2t-2,31) Показано на рисунке. 5,24. Существуют следующие качественные показатели: tp «= 0,635 с и а = 27%.
Следовательно, система соответствует требованиям с использованием выбранного последовательного корректора. Однако обратите внимание, что показатель качества скорректированной системы значительно отличается от расчетного значения (tp = = 0,5 с; a = 20%). Это объясняется недостаточным расстоянием полюсов s3 и s4 (см. Рис. 5.23) от пары определения комплексных сопряженных полюсов. В результате настроенные системные полюса имеют следующие значения: si.a = –4,5 ± 12; с. => —34,5, пара комплексных сопряженных полюсов, в отличие от выбранного (решающего) полюса, полюс s3 влияет на динамику системы.
Смотрите также:
Решение задач по теории автоматического управления

