Оглавление:


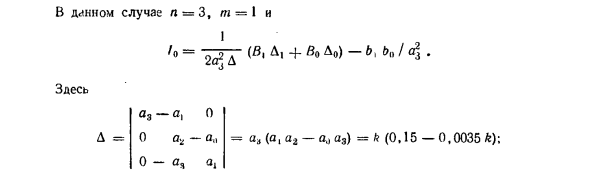


Выбор параметров по минимуму интегральной оценки
- Выбор параметров, которые минимизируют общую оценку Ранее (см. § 4.7) было установлено, что интегральная оценка использовалась для определения качества нормативных актов. Квадратичная интеграция 00 Оценка / 0 = \ x ~ dt дает представление об отклонении перехода Характеристики от идеала (ступенчато). Вторичное улучшение 00 Интегральная оценка /, = j * (x2 + T2x2) dt указывает на отклонение о Переходный отклик от показателя постоянной времени T Чем меньше значение / 0 или /, тем ближе переходный отклик к идеальному или экспоненциальному соответственно.
Параметры системы также выбираются с использованием минимальной интегральной оценки. Предположим, вам нужно выбрать параметр a для известного значения всех других параметров системы с квадратичной интегральной оценкой / минимальным значением 0. Вам нужно создать выражение / 0 и присвоить ему значение известного параметра. Тогда квадратичная интегральная оценка f0 является функцией одного параметра a, f0 = f0 (a). Значение, соответствующее минимальному значению функции / 0, определяется из уравнения д / 0 (а) / да = 0. (5,35)
После этого необходимо подтвердить, что (5.35) является минимальным условием функции / 0 (a). Это для значения а d2 / 0 (a) / yes2> 0. Людмила Фирмаль
В этом тесте может быть удобнее вычислять / 0 с двумя смежными значениями (большим и меньшим), а не только с найденным значением a. Последние два значения / 0 должны быть больше первого значения. Вышесказанное верно, если производные g / 0 (aYuda и g210 (a) / da2 существуют для всех допусков a. Функция fn (a) имеет наименьшее значение в пределах допуска a В граничном значении a (максимальное значение и минимальное значение) выберите значение, соответствующее нижнему значению „. • Вы можете выбрать два параметра a и a одновременно. В этом случае после подстановки числового значения всех известных параметров / 0 = / 0 (a, 0) в формулу / 0.
Требуемое значение параметра cal определяется по уравнениям одновременности. (5,37) d / 0 (a, k) / yes = 0; d! 0 (а, р) / др = 0, Если эти уравнения действительно соответствуют минимальному значению функции / 0 (а, (3), а и (3). Аналогичным образом выберите параметр a или параметры a и 0 с улучшенной квадратичной оценкой / минимум 4. Наиболее сложным этапом расчета является составление формулы / 0 или 11 (соответствующая формула приведена в п. 4.7). Удобнее создать формулу / 0 или / 4, заменив значения известных параметров в дифференциальном уравнении (или передаточной функции) системы. Пример 5.1. Добротность системы следует выбирать из минимального значения квадратичной интегральной оценки.
- Его функция передачи с открытой цепью (5,36) с (0,005 с-0,15 с-ф 0 Построить передаточную функцию замкнутой системы a, s * -f a, s — {- aj + a, b0s -f- bx Здесь «= 0,005; a = 0,15; a ^ a = 1 + 0,01 *. A3 = k, b0 = * 0,01L; = k. В этом случае n = 3, m-1 и 1 = 2? T L | + Lo) ~ b ‘b °’ ^ ‘ здесь = in «(a.» 2-o ^ vz) = * (0,15-0,0035 л); а, а, о О, о-о-о, D = o-i (Oi a2-o0 as) + a \ aj = 0,15 + 0,0205 футов — 0,000035 фут2; ag-x O az a2-ao O — a3 в Любовь a9 a2 0 0 a9-a0 0 0 a, b * = k *; B0 = bl = 0,0001 фут2. = ах а = 0,15 л2; К = в Определение / 0 / o = (150 + 17,5 футов + 0,05 футов 2) / | футов (300-7 футов)]. вычисляет производную от / 0 в футах dljdk = «(-9 + 0,42 фута -f 0,0275 фута 2) / | 2 фута 2 (3-0,07 фута)»]. Когда 0.0275ft2 4- + 0.42ft -9 = 0, производная исчезает (в конечных футах). Решение этого квадратного уравнения дает ft ^ 12. Вычисляет / 0 для значения, смежного с найденным значением фута. Когда ft = 12/0 = 0,142. фут = 10/0 = 0,143; фут = 14/0 = 0,143. 1,2 т, с
Можно сделать вывод, что добротность k => 12 фактически соответствует минимальному значению квадратичной интегральной оценки. На рисунке 5 показан переходный отклик системы при этом значении m k. 5,21. Показатель качества: a-42%; / p = 1,19 с. Чрезмерное регулирование — это здорово. Поэтому он пытается выбрать k как минимум улучшенной квадратичной интегральной оценки. f] = f0- * * T1; T — экспоненциальная постоянная времени. / ‘= CD = 1хЧ (рассчитывается так же, как квадратичная интегральная оценка, о Передаточная функция ((S) = (b <& + M / (a0s * + ais2 + a3). Определитель D для вычисления f ‘такой же, как вычисление f °.
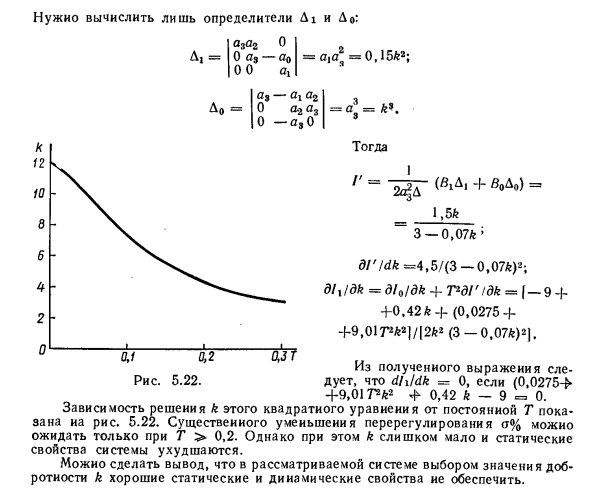
Здесь m = 2, но 62 = 0, поэтому B0 и B1 остаются неизменными, а B1 = 0. Людмила Фирмаль
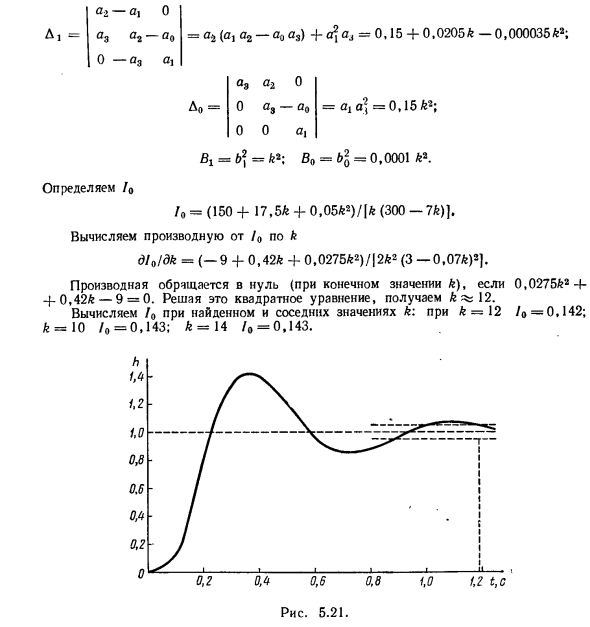
Просто рассчитайте детерминанты Dx и D0. 1 a3a2ОЛ, = 0 a9-a0 Я 0 0 -0,15 фута «; a, -ah ag O a2a3 O-a, O <= футов. 9 тогда / ‘= 2o * D 3-0.07ft ‘ d / ‘/ dft = 4.5 / (3-0.07ft) 2; d /, / dft = d / 0 / dft + T * dl’! dk = (-9 4-4-0,42 фута (0,0275 -1-9,01Г2 фут2) / 12 футов 2 (3-0,07 фута) 2). Из полученного выражения: 5,22. (Если 0,0275>, то dh / dk = 0 4-9.01 T ^ ft2 + 0.42 ft-9 = 0 На рисунке 2 показана зависимость решения ft этого квадратного уравнения от постоянной T. 5,22. Существенного снижения перерегулирования на% можно ожидать только при Т> 0,2. Однако фут слишком мал, и статические характеристики системы ухудшаются. В рассматриваемой системе можно сделать вывод, что выбор коэффициента качества ft не обеспечивает хороших статических и динамических свойств. (H, D, + H0D0) 1,5 фута
Смотрите также:
Решение задач по теории автоматического управления

