Оглавление:





Выборочная ковариация
- Выборочная ковариация Выборочная ковариация является мерой взаимосвязи между двумя изменениями. Объясняет эту концепцию на простом примере. После нефтяного кризиса 1973 года реальная цена на бензин, то есть цена на бензин, Из-за общего уровня инфляции он значительно увеличился, Значительное влияние на потребительский спрос.
- Изучите таблицу данных. B.1 В последнем приложении к книге вы можете увидеть его В 1963 и 1972 годах потребительский спрос на бензин неуклонно рос. Это Тенденция прекратилась в 1973 году и продолжала колебаться нерегулярно Спрос немного снизился в целом. В таблице. 1.1 дается Информация о потребительском спросе и реальных ценах после нефтяного кризиса.
Общая стоимость была рассчитана путем деления индекса номинальной цены на бензин. Людмила Фирмаль
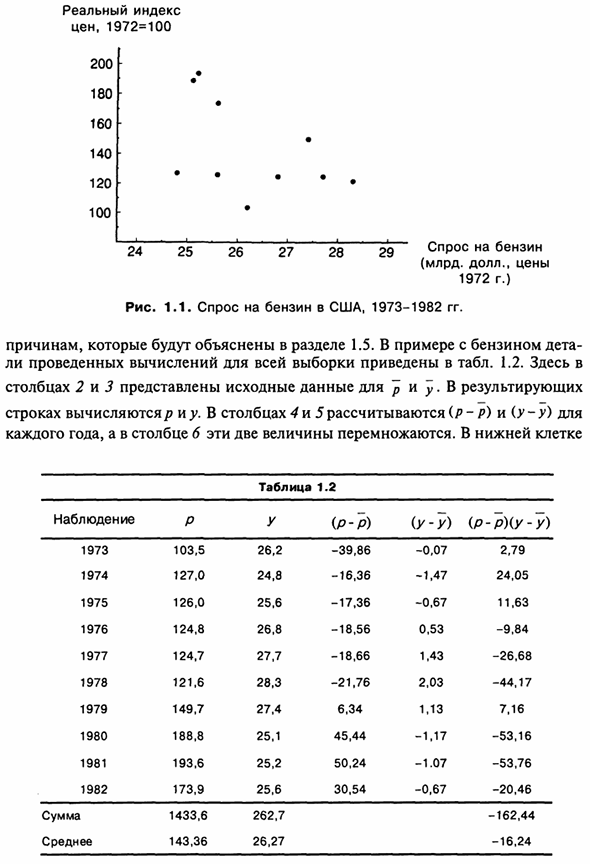
Приведено в таблице. B.2, Общий индекс потребительских цен из той же вкладки Умножьте результат на 100. Индекс в таблице. Б.2 На основании данных 1972, следовательно, фактический индекс цен таблицы. 1.1 выше Цены на бензин относительно общей инфляции с 1972 года) Рисунок 1.1 Эти данные показаны в виде точечной диаграммы. Смотри Потребительский спрос на бензин и Его реальная цена.
Выборочный индекс ковариации может представлять эту связь Для подсчета числа сначала находим среднее (учитывая Период выборки) Цена бензина и значения спроса. маркировка p и y определяются ценой через p и спросом через y. В этом примере он равен 143,36 и 26,27 соответственно. для Поэтому для каждого года рассчитайте отклонение p и y от среднего значения, Умножьте их. Первый год (р-р) равен (103,5-143,36) или -39,86, а (у-у) (26.2-26.27) или -0.07, а произведение (p-p) (yy) составляет 2,79.
Сделайте это для всех лет в выборке, чтобы получить среднее значение. Избирательная ковариация (как видите, не сложно рассчитать). определение Пример ковариации, если существует n наблюдений двух переменных (x и y) Соотношение между х и у дается C0V (X,)>) = — £ (* / — *) 0> / -Y) = — {(X, -X) 0> / -Y) + … + (Xn-X) (yn- у)}. (J],) n / = i p Замечания 1. Раздел 1.4 также определяет ковариацию общих переменных. Масса.
Используйте обозначение, чтобы различать эти две ковариации Cov (x, y) в верхнем регистре C для выборочной ковариации и Население ковариация между cov (x, y) -xy и населением в целом. иногда Последний обозначен для удобства. Подобные обозначения мы используем Также используется для дисперсии: Var (x) -в отношении дисперсии образца И поп. var (x) -популяционная дисперсия (теория).
Примечание 2: в некоторых учебниках пример ковариации похож В случае селективного распределения оно определяется делением на (n-1) вместо n причин, как описано в 1.5. Пример бензина Показывает ли таблица расчеты, выполненные по всей выборке. 1.2. здесь Столбцы 2 и 3 показывают исходные данные для p и y. В результате Ряды рассчитываются с p и y. В столбцах 4 и 5 рассчитаны (p-p) и (y-y) Каждый год эти два значения умножаются в столбце 6.
Среднее значение (–16,24) определяется в ячейке под последним столбцом. Выборочная ковариация. Обратите внимание, что в этом случае ковариация отрицательна. так Должно быть так. Как и в этом случае, негативные отношения Выражается хотя бы отрицательной ковариацией и позитивными отношениями Ложная ковариация. Имеет смысл рассмотреть эту причину.
Рисунок 1.2 точно такой же Рис 1.1, но здесь наблюдаемая диаграмма рассеяния делится на четыре части Вертикальные и горизонтальные линии, проходящие через Рю, соответственно Конечно Пересечение этих линий образует точку (p, y) и указывает на среду Цена и средний спрос за наш соответствующий период Boruke. Используя аналогию из физики, этот пункт Центроид набора точек, представляющих наблюдение.
- Для наблюдений в квадранте А, фактическое значение цены Спрос выше соответствующего среднего значения. Для данных наблюдений (P — />) и (yy) положительны, поэтому должно быть поло Исполняемый файл и (r-r) (y-y). Наблюдение, таким образом, становится положительным Вклад в ковариацию. Так, например, наблюдение 1979 года находится в этой четверке rnte и (rr) = 6,34, (уу) = 1,13, и их произведение равно 7,16.
Далее рассмотрим квадрант Б. Здесь фактическая цена наблюдаемого значения выглядит следующим образом. Среднее и спрос выше среднего. Следовательно, (р-р) является отрицательным и (у-у) Конечно, произведение (p-p) (y-y) отрицательно, и наблюдение вводит отрицательное Ценный вклад в ковариацию.
Например, в 1978 году (rr) = = -21,76, (уу) = 2,03 и (р-р) (уу), таким образом, равный -44,17. Людмила Фирмаль
В квадранте C как фактическая цена, так и спрос ниже среднего, колено (p-p) и (y-y) оба отрицательны, (P-p) (у-у) положительно. (См. Пример наблюдения за 1974 г.) Наконец, в квадранте D фактическая цена выше среднего, а спрос ниже среднего Go. (Р-р) положительный, (у-у) отрицательный, поэтому (P-p) (y-y) отрицательно, и отрицание вводится в каждую ковариацию Общий вклад. (См. Наблюдения 1981 года для примеров.)
Поскольку выборочная ковариация является средней (P-p) (y-y) В 20 наблюдениях Положительные вклады преобладают над отрицательными, отрицательные, если отрицательные Отрицательные вклады являются доминирующими. Активный вклад Квадранты A и C и ковариация, вероятно, будут положительными Основное распространение в гору. Аналогично отрицательный Вклад поступает из квадрантов B и D. Поэтому основное рассеяние Как и в этом примере, если вы наклоните вниз, ковариация, вероятно, Negative.
Смотрите также:

