Теория вероятностей и математическая статистика. Основные понятия

Теория вероятностей и математическая статистика. Основные понятия

• Теория вероятностей И математическая статистика Основные понятия В экономических проблемах приходится сталкиваться с двумя Тип явления. Первый тип неслучайный феномен, второй Random. Что такое неслучайное явление? Повторение в тех же условиях даст тот же результат. Повторные явления при одинаковых условиях Приводит к другому результату, который называется случайным.

• Наука для изучения моделей случайных явлений, Это называется теория вероятностей. Все последствия этого явления называются событиями. Событие Может быть: -Надежно, то есть неизбежно приходит В каждом тесте; -Не возможное, то есть то, что не может быть раскрыто Что происходит; -Случайно, т.е. в результате Будь тест сделан. Степень этого или его случайного появления Событие называется вероятностью.

Вычислить некоторые вероятности напрямую Задача исходит от частоты (P * (A)) м P (A) = -, (3,84) Где m — количество интересующих событий. Людмила Фирмаль

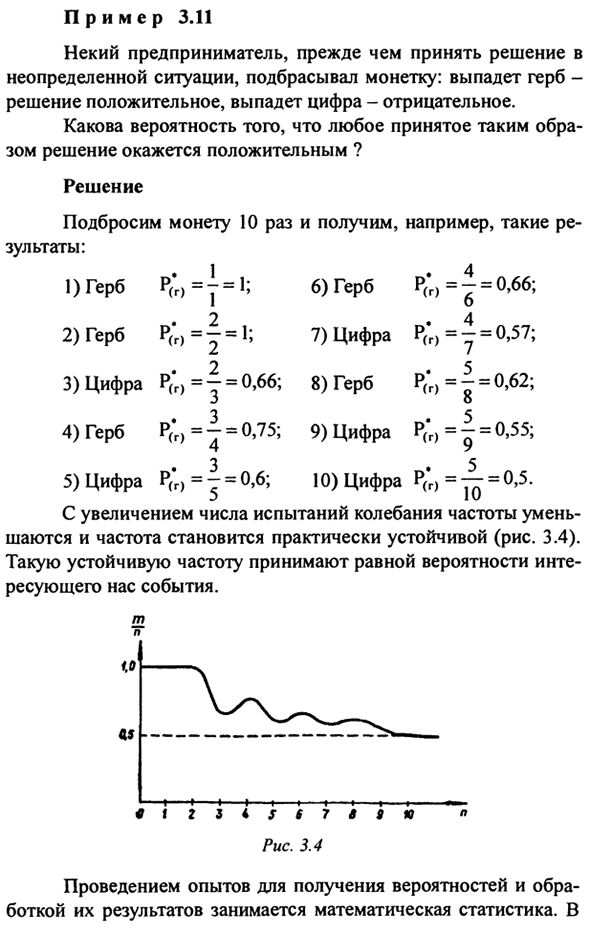
η- Общее количество тестов (эксперимент). Пример 3.11. Конкретные предприниматели, прежде чем принять решение о Неопределенная ситуация, бросил монету: эмблема падает- Решение положительное, а число выпадает отрицательно. Какова вероятность того, что каждый принял такую ​​вещь Так что решение положительное? Решения Бросай монеты 10 раз, например Результат:

1) Герб с гербом Р (* г) = — = 1; 6) Герб П (* г) = — = 0,66; 1 o 2) Герб с покрытием P (* r, = | = 1; 7) Цифра P (‘r) = — = 0,57; 2 5 3) число P (* g) = — = 0,66; 8) герб с гербом P (g) = — = 0,62; 3 O 4) герб P (‘r) = ^ = 0,75; 9) число P (* r) = | = 0,55; 3 5 5) Число P (‘r) = — = 0,6; 10) Число P (* g) = — = 0,5 По мере увеличения количества тестов изменения частоты Оно уменьшается и частота практически стабилизируется (рис. 3.4).

Такая стабильная частота считается равной вероятности Интересное событие. к 45 ‘■ ”ιι <> ι1 1— t— ZZiS67S9 » * ф Для иллюстрации Проводите эксперименты, чтобы получить вероятности Эти статистические данные обрабатываются математической статистикой. в Пример броска монеты, количество экспериментов Монета подбрасывается случайным образом: реально получается Достоверное значение вероятности, это число Намного больше Вероятность частоты.

• Это результат опыта, а вероятность — это предсказание. На основе частоты, так называемый Формула вероятности: πι P (A) = -> (3,85) Где m — количество возможностей, благоприятных для появления интересующего человека. Наше событие; η — общее число равных вероятностей. Пример 3.12. По статистике, когда вы инвестируете Прибыль на 100 000 единиц капитального строительства составляет Мы получили 18 случаев из 90 случаев.

Какова вероятность возврата инвестиций 100 000 строится? Решения Вероятность рассчитывается по следующей формуле: Количество выигрышных дел18 Всего равных возможностей 90 Пример 3.13 Многие были воспитаны в пруду. Подумай о том, что ты можешь сделать Считайте эту рыбу, не выпуская воду из пруда.

Решения Сначала поймать и поймать 100 карпа Отпустите обратно. Людмила Фирмаль

Затем дайте рыбе время осесть и снова поймать 100 Подсчитайте число, помеченное между пс и их. Например, Четыре рыбы были найдены. Это означает, что 4% прудовых рыб помечены. Но с другой стороны, я знаю, что есть 100 помеченных рыб. На самом деле, на 100 карпов приходится 4% от общего количества рыбы. Пруд; означает 100% 1ΛΛ100% _ΛΛ ^ 100 = 2500 рыб. 4% Используя формулу, аналогичную (3.85), расчет выполняется следующим образом:

Называется «геометрическая» вероятность Геометрическое представление симметрии и пропорциональности. Пример 3.14 На территории компании произошел несчастный случай Водоснабжение Общая длина водопровода L = 150 м. В том числе 50 м трубы (/) Занимает недоступное место. Насколько вероятно, что потребуется ремонт?

Вы в недоступном месте? Решения P = 1 = ^ — = 0,33. L 150 Та же геометрическая вероятность может быть рассчитана Генерировать только для равномерного распределения Все возможные выгодные возможности. Сформулируйте основные характеристики вероятности Следующим образом: 1.

Вероятность случайного события представляет собой число Положительный: 0> 0 (A) -yj ‘ 2. Вероятность достоверного события равна 1. P = 1. (А) 3. Вероятность невозможного события равна 0. Ρ <ν> = ° 4. Вероятность того, что произойдет случайное событие Предел между 0 и 1 0 <P (A) <1.

Смотрите также:

• Решение экономико математических методов

Нелинейное программирование (планирование)	Основные теоремы теории вероятностей
Динамическое программирование (планирование)	Случайные величины и их характеристика