Повышение точности в установившихся режимах

Повышение точности в установившихся режимах

• Улучшенная точность в устойчивом состоянии В системе контроля отклонений есть три элемента для установленной ошибки * Рот = 4sg + * usg + V, (5.I) Где l: ^ — ошибка воспроизведения основного действия. x «st — ошибка, вызванная внутренними и внешними помехами — ошибка чувствительного элемента, измеряющая несоответствие. Компонент * соотв. Если поведение вождения при t> 0 является довольно гладкой функцией времени (только конечное число его производных существенно отличается от нуля), воспроизводимая ошибка установившегося состояния Где C0, Cb C2, Cg … — коэффициенты ошибки воспроизведения, которые рассчитываются передаточной функцией Wx замкнутой системы для ошибки воспроизведения. Sg gd ‘Wx I г! [dsr J $ = o ‘

Ошибка стационарного состояния от каждого возмущения может быть выражена в виде ряда, аналогичного ряду (5.12). Коэффициенты погрешности С0 /, Cif, Су, Сг /, … по возмущению рассчитываются по передаточной функции Wf замкнутой системы для этого возмущения. Crf = \ d’Vf 1 r \ (dsr Js = 0 В статической системе С0 = 1 / (1 k) yС0 / = V (1 + kh (5 13), где k — коэффициент передачи открытой системы, а kf — коэффициент передачи прямой цепи от возмущения к контролируемым координатам. В результате достигаются постоянные значения поведения привода и снижение ошибок установившегося состояния при возмущениях.

Разница в передаточном числе без обратной связи. Людмила Фирмаль

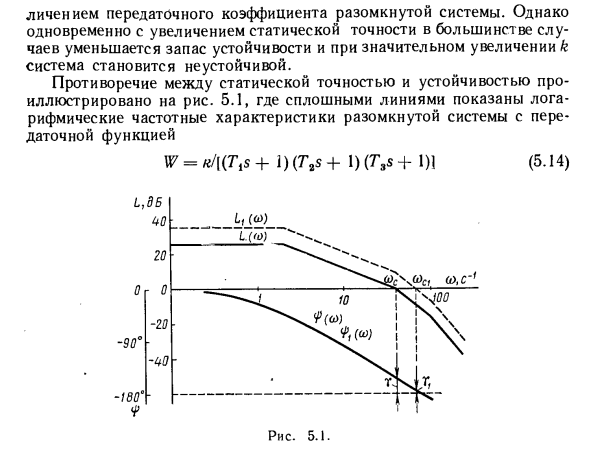
Однако одновременно с улучшением статической точности в большинстве случаев запас устойчивости уменьшается, и, если k значительно увеличивается, система становится нестабильной. На рисунке показано противоречие между статической точностью и стабильностью. 5.1 сплошной линией показаны логарифмические частотные характеристики открытой системы с передаточной функцией (5,14) Число = «/ [(7’1s + i) (7V + 1) (T9s + 1) 1 L, d5 UO L, (a>) -9C Рисунок 5.1. к = 20. G = 0,5 с, Tt = 0,025 с, T3 = 0,01 с. Когда передаточное число увеличивается до k = 60, частотная характеристика логарифмической амплитуды занимает положение, обозначенное пунктирной линией. Частота среза увеличилась, а запас по фазе уменьшился с cy = 26 ° до yi = 3 °.

Такой небольшой запас по фазе не совсем приемлем. Увеличение статической точности за счет увеличения коэффициента передачи открытой системы k потребует мер для обеспечения достаточного запаса устойчивости. Они описаны в следующем абзаце. , Вообще говоря, вы можете создать структуру системы, которая может неограниченно увеличивать передаточное число k (2) в разомкнутом контуре. Еще один способ повысить статическую точность — обеспечить астеризм. В статических системах снижение частоты ошибок имеет следующие последствия: C0 = 0; C, = \ / kv: C0 / = 0; Ct / = kflkc, Где kD — коэффициент передачи в разомкнутом контуре, в этом случае называется коэффициентом скорости системы (или коэффициентом скорости скорости). Таким образом, статическая система была создана

• Ошибки из-за постоянного вождения и постоянных помех. Путем введения интегрированных связей в прямую цепочку систем достигается астеризм. В статическом состоянии по отношению к помехам должна быть введена интегрированная связь в точке, где применяются помехи (рисунок 5.2). На рисунке показано, как интегрированная ссылка влияет на динамические характеристики системы. 5.3 сплошной линией показаны логарифмические частотные характеристики системы с использованием передаточной функции f (5.14). Когда модуль интегрирования вводится в разомкнутой цепи этой системы, характеристика занимает положение, обозначенное пунктирной линией.

Фазово-частотная характеристика сместилась вниз на -90 °, а амплитудно-частотная характеристика повернулась по часовой стрелке вокруг точки а. В результате запас устойчивости фазы был уменьшен с y = 26 ° до недопустимо малых значений y! = 6 °. Система остается стабильной, но переходный процесс очень колебательный. Кроме того, частота отсечки снижается, а переходный процесс удлиняется. Рисунок 5.2. Рисунок 5.3.

Однако в других ситуациях внедрение интегрированных ссылок не только ухудшается, но может даже улучшить динамические характеристики системы. Людмила Фирмаль

Например, значение постоянной времени для системы, использующей передаточную функцию (5.14): Ti = 0,05 с, T2 = 0,0025 с, 7 * с = 0,001 с. На рисунке показаны логарифмические частотные характеристики открытой системы. 5.4 Сплошная линия. С введением интегрированной ссылки характеристика находится в положении, указанном пунктирной линией. В этом случае интегрирующая линия снизила частоту среза, но увеличила запас по фазе. Считайте от f = 219 до ji = 43 °. Скорость системы уменьшается, но вибрация также уменьшается.

Следовательно, повышение статической точности за счет предоставления статистики с использованием интегрированной ссылки может привести к снижению производительности системы и может потребовать мер по поддержанию запаса устойчивости. Л.95 40 20 O O -180 * -20-40 L ((D) ШС1, б), С- ‘ % (<*) \ 100 \ iooo L \ \ ! \ ^^ я \ w _____ A GL Рисунок 5.4. -90 ‘ Обеспечение статистики с использованием изодомной связи, то есть передаточной функции Hnz = kH (Tns-l) / s =] + kjsy, дает значительно лучшие результаты. Где Ty = \ / kB — постоянная времени изотопа. Рисунок 5.5. Если постоянная времени достаточно велика, запас устойчивости можно сохранить без изменений.

Уменьшение передаточного числа разомкнутого контура должно быть компенсировано увеличением передаточного числа другого звена (скорее всего, усилителя). Обратите внимание, что более высокие значения T могут увеличить наивысшую частоту ошибок. Системная статистика по основным действиям может быть предоставлена ​​очень простым способом: неединичная обратная связь и масштабирование (3). Блок-схема системы с неединичной обратной связью показана на рисунке. 5.5 а. В устойчивом состоянии регулируемая координата // связана с действием постоянной настройки g0 посредством отношения. Y = k „Яо (5.15)

Где ka — прямое передаточное число системы. Выполнение основной обратной связи системы с использованием коэффициента передачи k0 = 1- \ / kn приводит к y = g0, и система статична по отношению к ведущему действию. Блок-схема системы с масштабированным вводимым количеством показана на рисунке. 5.5.6. Его особенностью является то, что на входе имеется усиление с передаточным отношением m. Устойчивое состояние y = mg0k / (1 4- (5,16) Где k — передаточное число без обратной связи. Если m = 1 + l / k, то y = g0 и система статична по отношению к основному действию.

Недостатком этих способов является то, что астеризм гарантирован только при сохранении заданного соотношения между передаточными числами. Неточное определение передаточного числа любого элемента системы и его изменение во время работы приводит к появлению статических ошибок. Даже если параметры системы изменяются, астеризм, достигнутый с помощью интегрированных или изодомных ссылок, сохраняется. Введение двух интегрированных или изодомных связей в систему дает астеризм второго порядка. В этом случае C0 = C, = 0; C2 = 1 / заряд; C0 / = Clf = 0; C2 / = kf / kt>, где kt — коэффициент передачи открытой системы, в данном случае система ускорения

Это называется качественным фактором (или качественным фактором). В системах, использующих статистику второго порядка, нет основных действий и ошибок стационарного состояния из-за возмущений, которые являются постоянными по величине и изменяются с постоянной скоростью. Однако два последовательно соединенных интегрированных звена делают одноконтурную систему усиленных, апериодических и колебательных звеньев структурно нестабильной. Следовательно, необходимо изменить структуру системы, чтобы она была структурно стабильной и обеспечивала необходимые запасы устойчивости. Можно гарантировать беспорядок и высший порядок. Кроме того, был введен ряд интеграций

Смотрите также:

Решение задач по теории автоматического управления

Оценка качества регулирования в установившемся режиме (коэффициенты ошибок)	Обеспечение устойчивости и повышение запаса устойчивости
Общие соображения	Корректирующие устройства