Методы оптимизации: линейное программирование

Методы оптимизации: линейное программирование

• Метод оптимизации: успех линейного программирования с подавляющим большинством Экономические проблемы зависят от лучших и самых выгодных методов Использование ресурсов. В процессе хозяйственной деятельности Вы должны выделить важные ресурсы, такие как деньги Продукты, сырье, оборудование, труд и т. Д. И как они Они обычно распределяются?

• Зависит от ограниченных ресурсов Конечный результат деятельности, бизнес. Суть метода оптимизации заключается в Этот метод выбора зависит от доступности конкретного ресурса Использование (распространение), предоставление Самый большой (или самый маленький) показатель интереса. Это учитывает определенные ограничения, Он налагается на использование ресурсов в зависимости от условий экономической ситуации.

Метод оптимизации в экономике Применение всех основных разделов математики. Людмила Фирмаль

Программирование (планирование): линейное, нелинейное, динамическое. Линейное программирование (планирование) Линейное программирование (планирование) — Математический метод определения максимальной или минимальной линейности Функции с ограничениями в виде линейных неравенств, или Уравнение.

Здесь линейный означает, что функция нарисована в форме прямой линии, представляющей первый порядок на графике. Соответствующее количество. ) Максимизировать (минимизировать) функцию Представляет принятые критерии эффективности в решении проблем, Подходит для цели. Называется цель Функция. Ограничения характеризуют имеющиеся возможности Решение проблемы.

Сущность решения задач линейного программирования Это найти условия, чтобы полностью изменить цель Минимальная или максимальная функция. Решения, отвечающие требованиям проблемы Достижение поставленной цели называется оптимальным планированием. Использование линейного программирования (планирование) Выбор лучшего ограниченного плана распространения Аналогичный ресурс для решения проблемы.

В общем, постановки для линейных задач Программирование выглядит следующим образом: Условия задания представлены с использованием системы Линейные уравнения или неравенства, представляющие ограничения, Взимается плата за использование доступных ресурсов: allxl + a12x2 + … + ayxj + … + alnxll = bI; a2i * i + a22 * 2 + … + aL + … + a2nxn = b2; (3.1) ailxI + ai2 * 2 + … + aijxj + … + ainxn = bi; am, x, + a ^ x2 + … + a ^ + … + amx = bx; j = 1,2, …, n; i = 1,2, …, m; m 09

Где х. -Целевое значение, включая набор решений Задача а. И К — известные постоянные значения, Охарактеризуйте состояние проблемы. Целевая функция (линейная форма) определяется как: y = c, *, + c2x2 + … + c] X. + … + shp1 J-I.2 n, J Где с постоянный фактор (фактор стоимости). Вы также можете указать условия задачи (пределы) Неравенство формы. В этих случаях вы можете привести систему.

Линейные ограничения на форму (3.1), введенные для каждого выравнивания Дополнительный неотрицательный неизвестный лимит: * η + 1 ‘* η + 2’ * … ‘* η + ιτΓ Целью оптимизации является Уменьшите ожидаемую стоимость, чтобы решить эту проблему Минимальная компания. Общая математическая постановка задачи Условия (3.1) и (3.2). Первая строка одновременных уравнений (3.1) a ,, *, + a.jc, + … + a, x + … + a, χ = b, 121 12 2 lj) Inη1

Смысл этого примера заключается в следующем: ap-число единиц ресурса первого типа 1 Предприятие; A12-2 Количество единиц ресурса типа 1 Компании и т. Д. B — общий ресурс ресурсов типа 1 (все компании). х], х2 и т. д. — требуется количество компаний типа 1,2 Во второй строке приведенных выше уравнений Аналогичная по значению целевая функция для таких ресурсов, как тип 2 Соответствует уравнению (3.2). Требуется минимум у = с.х. + c, x, + … + cx + … + cχ, 7112 2 IIηη ‘

Где с — это индекс, который характеризует стоимость компании. Пусть m будет общим количеством различных типов ресурсов, Находится в собственности владельца, n — количество типов компаний, Вам нужно распространять эти ресурсы. В то же время Вы знаете, сколько похожих ресурсов разных типов (I = 1,2 … м) Может быть реализовано каждой компанией Помимо этого типа (j = 1, 2 … η), общий объем ресурсов (B) этого типа.

Относительная величина также известна. Стоимость каждой компании. Задача состоит в том, чтобы сделать лучшее Способ распределения доступных ресурсов между компаниями, т.е. Найти неизвестное количество χ-необходимое для этого количества Это тип компании. Пример 3.1 У владельца есть четыре типа ресурсов (t = 4). Это могут быть, например, денежные средства, промышленные объекты, Оборудование, сырье.

Ресурсы 6 компаний (n = 6). бизнес Экономические условия деятельности: местонахождение, Налоговая система, стоимость энергии , Оплата и т. Д. Поэтому производственные затраты разные. относительный Уровень затрат для данной таблицы. 3.1. Таблица 3. J Относительный уровень корпоративных затрат компании стоимость 1 0,4 2 0,5 3 0.2 4 0.8 5 0.6 6 0,3 Распределять ресурсы по компаниям, Необходимость учитывать множество возможных ограничений.

Описывается системой из четырех уравнений с шестью неизвестными, Аналогичная система (3.1): Первый тип ресурса 4dg, + x4 = 16; Ресурс второго типа 2×2 + x5 = 10; Ресурс третьего типа x3 + 2×4 + 6×5 = 76;> Ресурс 4-го типа 4x {+ 3l; 2 + l; 6 = 24; » ^> 0 (j = 1,2, …, 4). J Значение первого уравнения в этом примере Ресурсы типа 1 в общей сложности 16 единиц Расположенный в количестве 4 единиц в компании. Первый тип и одна единица — четвертый тип предприятия.

Аналогично, смысл второго и последующих уравнений становится понятным. Последнее условие заключается в том, что количество компаний Может быть отрицательным. Необходимо определить количество компаний Каждый тип требует общей стоимости Минимум. По данным табл. 3.1 Целевая функция Оптимизация принимает форму у = 0,4х, + 0,5х2 + 0,2х3, 0,8х4 + 0,6х5 + 0,3х6. (3.4)

Решение проблемы состоит в том, чтобы встретить ограничения Определяется уравнением (3.3) с учетом условий минимизации Формула (3.4). В этом примере, когда η-m = 2, Ограниченные линейные уравнения (3.3) и линейные функции (3.4) Можно выразить геометрически в двух измерениях Космос (на плоскости). Выразить ограничения и целевые функции Расписание, вы должны выразить все известное самостоятельно Количество.

Например, χ1 и x2 соответствуют координатным осям Какая конструкция будет иметь место (рисунок 3.1). U ·. · -U? Из уравнения (3.3): jc3 = 8x, + 12×2 -16; х4 = 16-4 *; х5 = 10-2х2; х = 24-4 *. -Zh? , Целевая функция принимает форму ^ -2,4 ^ + 0,8 ^ + 22,8. (3.6) Из сравнения уравнения (3.5) и последнего уравнения Ограничение (3.1) Если r> 0: *,> 0; 1 х2> 0; x3 = 8x, + 12jc2-16> 0; х4 = 16-4х,> 0; , х5 = \ 0-2х2> 0; χ6 = 24-4χ1-3λ: 2> 0 Дж Каждому неравенству на графике рисунка (3.7) соответствует 3.1.

Полуплоскость, где все приемлемо Учитывая неравенство, значение переменной χ (j = 1, 2, …, 6). Таким образом, неравенство x}> 0 соответствует правой полуплоскости. От оси x2 (граница заштрихована). Неравенство x3 = 8xJ + \ 2×2-16> 0 равно Полуплоскость справа вверху от заданной граничной линии Неравенство (при х3 = 0). Уравнение этой линии 3 1 2 2 Точно так же вы можете построить границы, определенные ниже.

Другие уравнения. Неравенство (3.7) соответствует конкретному Шестигранник ABCDEF, образованный вышеуказанной границей Полуплоскость Эта область иногда называется областью. Приемлемый план, потому что любая точка в нем достигнута Требования к наложенным ограничениям (3.3). Я заинтересован в лучшем из всех приемлемых планов План, в котором целевая функция у достигает минимума.

Целевая функция соответствует параллельной семье Непосредственно. Рассмотрите один из них и пройдите первый Координаты сделаны при у = 22,8. X2 = xxg Как видите, интересующая линия у = 22,8. 3,1 Наклонена вправо от оси ху получить значение у, семейство прямых, параллельных прямой у = 22,8 проходит через точку 0.

Кроме того, меньший Поэтому очевидно, что значение у находится справа. Соответствующая линия. Чтобы достичь минимального значения у, Я заинтересован в самой большой линии Двигайтесь вправо от линии y = 22,8 и передайте многоугольник ABCDEF — это строка y ^. Единственная точка, которая соответствует оптимально План имеет вершины многоугольника ABCDEF (рис. 3.1).

В то же время относится к области возможного планирования, Соответствует требованию минимизировать целевую функцию y и вершину C. Из уравнения прямой BC, проходящей через точку C, х1 = 4 Из уравнения прямой DC, проходящей через одну и ту же точку, х2 = 0. X} = 4 и x2 = 0 уравнения, подставляющие полученные значения (3.5), определить значение оставшихся переменных Оптимальный план: χ3 = ιβ * 4 = 0; * 5 = 10; * 6 = 8.

Таким образом, оптимальный план выглядит следующим образом: *, = 4; ^ х2 = 0; х3 = \ 6; х4 = 0; л: 5 = 10; х6 = 8 Линейная форма (стоимость) Минимум: 24 A 8Λ228 132, „„ у = 4 + -0 + = = 13,2. (3 9) 10 10 10 10 K} На самом деле, есть несколько задач, таких как: Возможен пример, но нужно максимизировать целевую функцию (Например, доход или прибыль). При решении этих задач целевая функция рассчитывается В выражении, подобном (3.2): y = c>, + c * x, + … + c ** 3 + c> n, (3.10) Где у — целевая функция, которую нужно максимизировать. манок чьи.

Символ перед всеми константами Коэффициенты обратные (c * = -c *). Вычислительное линейное программирование Рассматривается геометрическая интерпретация проблемы Линейное программирование возможно только с двумя Независимая переменная. 3 переменные, визуальные В этом случае презентация очень сложная. Выпуклый многогранник в трехмерном пространстве, Соответствует сумме допусков плана.

Если количество переменных 3 или более, задача будет потеряна Геометрическая видимость, чтобы было трудно представить Например, четырехмерное пространство. Но получить идеи Из вышеуказанного решения Многомерное пространство. Исходя из этой идеи, один из основных Как решать задачи линейного программирования Это называется симплекс-метод.

Симплекс-метод является алгебраическим решением Задача линейного программирования, возникающая из Это считается геометрическим выражением. При демонстрации Симплексный метод опирается на вышеизложенное Для 2D вы можете просто переключиться Геометрическое представление алгебраической аналогии. Первый шаг Найти действующий соответствующий план Одна из вершин исполняемого плана области.

• Второй шаг Проверьте, является ли найденный план оптимальным. если Оптимальный расчет завершен. Если нет, то следующий план. Третий шаг. Переход на другой пик (другой Приемлемый план), если значение целевой функции мало, Проверьте на оптимальность Итак, первый шаг — получить координаты. Одна из вершин допустимого многоугольника (многогранник) План.

Для этого необходимо преобразовать уравнения одновременности Легко получить Координаты вершины многоугольника (многогранника) области Приемлемый план. Анализ рисунка 3.1, вы можете увидеть его в каждом Вершины двух переменных исчезают. Поэтому мы должны Возьмите две переменные, равные нулю, и найдите остальные Четыре системы уравнений (3.3).

В совокупности все переменные Предоставляет один из нескольких приемлемых планов допуска Топ. Людмила Фирмаль

Преобразовать описанную систему уравнений Поэтому необходимо представлять каждого из неизвестных xv xv …, xm. Через остальное. Такая возможность существует только в том случае, если: Предварительный конкурс Ха ,, а12 … а, т а2, а22 … а2т Если это условие выполнено, количество x] 9 x2, …, xm Это называется основным.

Каждая база соответствует Есть верх. Преобразовать систему уравнений (3.3) Сделать две переменные равными нулю (например, x5 = 0, x6 = 0) Получить значение базовой величины *, x2, x3 и x4-координаты Одна из вершин многоугольника. Во-первых, определитель Состоит из этих неизвестных коэффициентов в уравнении (3.3) Это не ноль. конечно «4 о о 4 P о 2 = 8 (3.12) Это дает вам право принимать значения *, x2, xg и x4.

Является основным и может решить систему (3.3) О них Выполните все необходимые преобразования Матрица коэффициентов уравнения (3.3): (4 0 0 1 O O 02 0 0 1 O D 0 0 12 6 0 7 1 ^ 4 3 0 0 0 1 2 Преобразовать матрицу (3.12) согласно инструкции Превышает требование для получения базового значения переменной Количество.

Для этого такой Преобразования, которые оставляют одну базовую переменную для каждого Из уравнения (строки матрицы) коэффициенты Равно 1 Начните с первого коэффициента χχ Уравнение. Разделите все коэффициенты, чтобы они были равны единице Четыре первых уравнения. Исключить переменную х1 Сначала вычтите оставшиеся уравнения из каждого из них. Разница в том, Коэффициент х равен нулю.

Например, второй и третий Уравнение (строка) должно быть умножено на ноль, четвертый и один. Результат преобразования выглядит следующим образом: 1 0 0 О 1 4 0 0 0 0 1 0 10 0 0 1 2 6 0 76 0 3 0-1018 (3.13) Выполните аналогичные преобразования для переменных Χ во второй строке: 1 0 0 0 1 0 0 0 1 4 0 2 0 1 6 0 0 0 4 5 76 Ах ах O -1- 1-7 (3-14) Для переменной x} в строке 3 и x в строке 4: (3 1 9 л 1 0 0 0 — 8 4 4 0 10 0-05 2 0 О Ах ах 1 о о

Поскольку 1—1 62 (3.15) Процедура, которая выполняется, называется полным методом Исключение (так называемое иорданское исключение). Где переменные х5 и х6 (соответственно Пятый и шестой столбцы матрицы) ноль, Значение базовой переменной. Равны в этом случае Свободный член соответствующего уравнения: 9 х2 = 5; * 3 = 62; х4 = 7.

Посмотрите на геометрическую интерпретацию (см. Рисунок 3.1). Вы можете видеть, что полученные координаты x] = 2V4, x2 = 5 x5 = x6 = 0 соответствует вершине A Полигон ABCDEF- Эффективная зона планирования. Это первый приемлемый план. Теперь вы можете перейти ко второму этапу симплекс-метода — Эффективный план Соответствует найденной вершине A и является оптимальной.

Самый естественный способ решить эту проблему Исчерпывающий поиск всех вершин в области возможного планирования, Определение каждого значения переменной r (j = 1, 2, …, 6) Их вычисление в каждой вершине значения целевой функции. Пик, где у Минимизируйте и предоставьте лучший план, который вам нужен. Однако этот путь очень неэкономичен, поскольку требует вычислений Многочисленные планы, в том числе и те, которые явно не оптимальны.

Следовательно, симплекс-метод не является непрерывным, Направленный перечень планов. План лучше предыдущего. Количество вычислений Операция значительно снижена. В чем суть направления перечисления? В первом плане допуска, соответствующем вершине A, Целевая функция согласно уравнению (3.6) эквивалентна: vA = -2,4l: + 0,8×2 + 22,8 = -2,4- + 0,8,5 + 22,8 = 21,4. 4 Из уравнения (3.9) мы уже знаем, что ymin = 13.2.

Следовательно, целевая функция в точке A намного больше минимального значения. И вам нужно продолжить поиск топ-плана Это не будет оптимальным. Вы можете перейти от вершины A к смежным вершинам F и B. (См. Рисунок 3.1), двигайтесь вдоль сторон многоугольника AF и AB Соответственно. Видимо, вам нужно выбрать направление этого перехода К следующей горной вершине Снижение целевой функции.

Вычислить значение целевой функции для смежных вершин F и B. Используйте формулу (3.6) и соответствующую Получите значения хх и х2. yF = -2,4 ± 0,8 ± 5 + 22,8 = 26,8; SW = -2,4 · 4 + 0,8 ·% + 22,8 = 15,33. Сравнение двух последних выражений не сложно Убедитесь, что минимизировали функцию цели при движении к AB боковая точка B. Это означает, что фонд был введен Переменная x5 равна нулю в вершине A.

Потому что нет четкой геометрии Просмотр значений переменных не может быть предварительно размещен Шины Polygon, и установить необходимость, В инструкциях по перечислению планов используется специальный критерий δ. м 5j = Xcia9 ~ ci «(3.16) я = я Где индекс j принадлежит неосновной (нулевой) переменной. Индекс я является основным. Чтобы получить значение коэффициента с.

Целевая функция yA преобразуется для исключения Тогда неосновные переменные х5 и х6: yA = -2,4 л:, + 0,8×2 + 22,8 = -0,8 л:, -, 6×2 + 0,2 * 3 + 0,8×4 + 72. Значение а. Выбрано из соответствующего столбца Матрица (3.15). Есть доказательства в случае оптимальности Все δ в результирующем проекте будут равны или меньше нуля. Переменная взята δ Наибольшее положительное значение.

В этом примере это: δ5 = с, а15 + с2а25 + с3а25 + с4а25-0 = Yu I） s） νioJ 2ίοίο2ίο δίβ- ±. ! -ϋ.0 + -? -. 2- ± (-1) -0-. *. 6 10 4 10 10 10 5 Поэтому мы приходим к тому же выводу Нужно включить в базу переменную х5 Критерий имеет наибольшее положительное значение. Затем вам нужно установить, какая переменная Выводится из основ введением переменной х5. Чтобы ответить на этот вопрос, рассмотрим эти причины.

Очевидно, что нужно двигаться так же вдоль AB Чтобы максимально уменьшить цель, дальше от точки А Функция. Таким образом, вы можете получить координаты χχ точки Максимальное значение, разрешенное системой Уравнение (3.5) соответствует матрице (3.15), то есть Ни одна из переменных не является отрицательной. Можно показать, что это достигнуто Вывод переменной, соответствующей минимальному значению из базы.

Положительное значение отношения свободных членов уравнения Коэффициент X5 соответствующего столбца матрицы (3.15). Поэтому четвертая строка матрицы выбрана, Следовательно, переменная x4 исключается из базы. Затем вам нужно получить значение в строке 4 Коэффициент с новым базовым значением х5, равным 1, Все остальные коэффициенты в этом столбце исчезнут. для Ознакомьтесь с полной процедурой расчета исключений.

Получить 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 2 3 0 0 0 1 0 1 3 4 2 3 4 8 3 48 14 3 (3,17) Эта матрица соответствует действительному плану для вершины B. Сделать неосновные переменные равными нулю (x4 = x6 = 0), Получить значение второй соответствующей оставшейся переменной К плану: * ι = 4; 8 χ? = х3 = 48; _14 v5 χ <= 3 ‘J 3 Как уже показано, ув = 1573. Таким образом, Значительное снижение целевой функции, но стандартное δ6

Продолжайте быть позитивным и показывать необходимость Дальнейшее улучшение плана: 3 «.—!; δ6 = 10 На этот раз на основе ввода Переменная x4 отображается и отображается Переменная x2, соответствующая минимальному значению x6 столбцовые коэффициенты. После преобразования матрицы (3.17) получаем матрицу (3.18), соответствующий третьему плану: Этот план соответствует пику C.

х {= 4; х4 = 0; х2 = 0; х5 = 10; * 3 = 16; х6 = 8. Критерий δ для этого плана равен Потому что нет положительного стандарта, Третий план оптимален. 3.1. Целевая функция этого плана: США = 13> 2 Так что аналитически стало то же самое Оптимальный план, полученный ранее геометрическим способом. Решение в Примере 3.1 может быть сформулировано следующим образом: Метод.

Стоимость распределения ресурсов между Количество компаний минимально, а количество компаний Первый тип — 4, второй — 0, третий — 16, 4–0, 5–10, 6–8. В этом случае стоимость составляет 13,2 единицы. Важно отметить, что это худший план доставки. Соответствует точке F, это приводит к потере 26,8 единиц. так Никаких дополнительных затрат на ресурсы, ресурсы (только для Разумное распространение) Улучшенные результаты решения Задача более чем удвоилась.

С учетом процедуры расчета Следует отметить, что система уравнений (3.3) решается следующим методом. Последовательное исключение неизвестных. За такое решение по математике Я применил устройство матричной алгебры хорошо. Выполните расчеты, которые вам нужны наиболее экономно. Метод решения системы уравнений (3.3)

Матрица выглядит следующим образом: Исходная система уравнений (3.3) может быть сделана компактной Он существует в виде матричного уравнения этой формы: AX = S, (3.19) Где A, X и S — некоторые матрицы. Матрица А содержит коэффициенты переменных Формула (3.3): (4 0 0 и 0 2 0 3 0 0 1 0 1 0 2 0 0 1 6 0 0 ^ 0 0 1 (3.20) Матрица X содержит переменные для следующего уравнения: х = V * 6 лет (3,21) S =

Матрица S содержит свободные члены того же уравнения. 16 год 10 76 Дж (3,22) 24j Уравнение для целевой функции (3.4) в матричной форме имеет вид Представьте себе, что: Y = CX, (3,23) C — матрица, содержащая коэффициенты переменных Формула (3.4) С = (0,4; 0,5; 0,2; 0,8; 0,6; 0,3). (3,24) Делит матрицы A, X и C на подматрицы (ячейки). — Первоначально (или согласно принятому основному решению Поддержка) планирование.

Матрица A делится на подматрицы A0 и As, а также A0 Содержит столбцы, соответствующие коэффициентам Переменные x5 и x6 равны нулю, а матрица As есть Столбец, соответствующий оставшимся коэффициентам (базовый) Переменная: A0 = ¿ 1 6 ° 1 0 0 υ (3,25) A = (A 0 0 0,4 0 2 0 3 0 0 1 0 \ 0 2 0 (3,26) Матрица X делится на подматрицы X0 и Xs, а также X0. Содержит значение переменной, равное нулю, aXs-значение.

Другие (основные) переменные: (3,27) (*, (0 \ Ур (Χχλ x2 * 3 {**) = ί161 10 76 [24 Дж (3,28) Матрица C является подматрицей C0 и Cs, а также C0 Содержит коэффициент в линейной форме формулы Нулевая переменная и оставшаяся (основная) переменная C: С = (0,6 0,3); (3,29) С = (0,4 0,5 0,2 0,8). (3.30) Подтвердите все полученные активные планы (включая Числовая и начальная) оптимизация выполняется с использованием Называется эталонный вектор D.

Критерием является следующий вектор Свойство: если оно содержит хотя бы один элемент Если положительный, соответствующий план не является оптимальным. Наличие Опорный вектор равен отрицательному или нулю Элемент указывает на оптимальность плана. Опорный вектор рассчитывается по формуле D = CR-C0; (3,31) * = α§- » α0, Где A ^ 1 — обратная 1 для матрицы As \

Есть доказательства в случае оптимальности План результатов, все элементы опорного вектора Равен или меньше нуля (см. Критерий δ выше). Проверьте первоначальный план, используя критерии Вектор. As_1 R = A8 «, A0 = 1 матрица B называется обратной квадратной матрицей Когда AB = 1 (1 — единичная матрица).

Обратная матрица А, Обозначается как А-1. C.R = i_ A A A 10 10 10 10 D = CR-C „ 10 10 ‘2 1 ^ № 8 4 1 o 2 3 2 2 V 2 f 6 • 1 3_ 10 10 10 десять J2_2 10 5, (3,32) 13 -> 0, поэтому первоначальный план не является оптимальным. 10 Перейдите к следующему шагу. Найти наибольший коэффициент из уравнения (3.32) 12 10 ‘ Соответствует введенной в базу переменной x5.

Далее переменные устанавливаются, как описано выше. х4 исключен из основ. Значение другой переменной рассчитывается по формуле где X = B-xD, B = A-S; (3.33) в 0 0 -2 1 3 Ϊ 1 ~ 2 -3 3 ~ 2 0 0 1 о 1 4 * 0 2 -] 16 год 10 76 v24y <9_L 4 5 62 7 ν, U G9 ‘ 4 5 62 v7y -0 = (9λ 4 5 62 17J Таким образом, было получено следующее значение Вторые улучшенные переменные планирования: _ 9_a * 1 ~ 4 ‘ х2 = 5; хг = 62; х4 = 1; * 5 = 0; * 6 = 0.

Это первый приемлемый план, с которым мы знакомы. Соответствует точке А на графике рисунка 3.1 и т. Д. Ниже приводится набор задач, которые можно решить с помощью Линейное программирование, показывающее возможности Это метод и решение. Пример 3.2 Рассмотрим конкретную производственную ситуацию. Например, трудоемкие механизированные организации Работает и имеет множество единых технических средств 30 единиц в трех местах: A, А, А3.

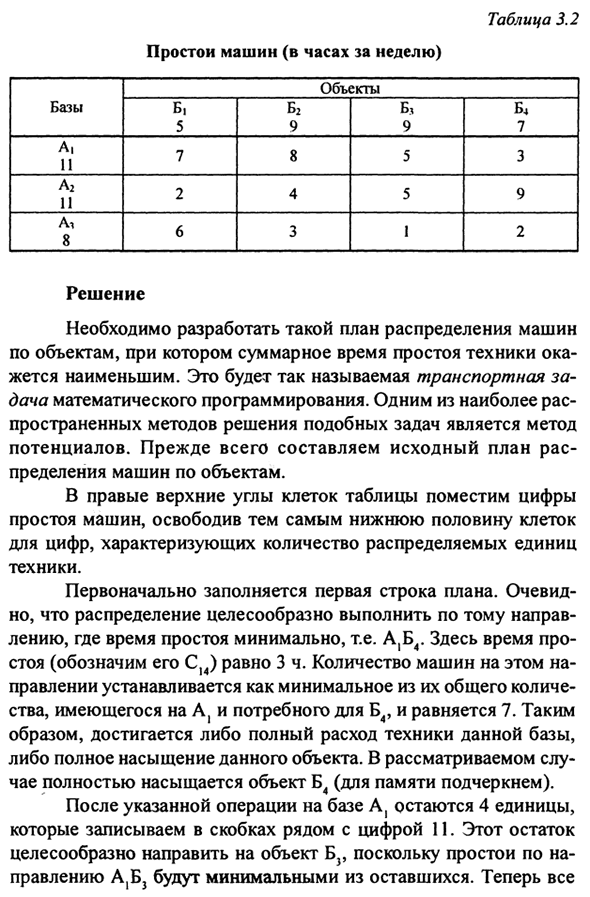
В то же время базы А и А2 имеют по 11 устройств, Базовый блок А3-8. Использование этой техники Четыре объекта B, B2, B3, B4. Кроме того, объект B требует 5 Единица, объекты B2 и B3- 9 единиц каждая, объект B4- С 7 единиц техники. Операционная эффективность технических средств Это сильно зависит от того, насколько интенсивно они используются. Чем короче время простоя, тем выше эффективность.

В этом случае Время простоя машины в основном Объект, где они работают. Например, базовые автомобили А3, занятые на объекте B1? На холостом ходу в среднем 6 часов в неделю, та же машина Объект B3 неактивен только один час в неделю. Общая ситуация и применение технологии использования В таблице показано расположение объекта и необходимость наличия. 3.2.

Решения Необходимо создать план распределения для таких машин Для объектов, где происходит полное время простоя оборудования Будет самым маленьким. Так называемый транспорт Вопросы математического программирования. наиболее Распространенным способом решения этих проблем является Потенциал. Сначала составьте свой первый план Распределение автомобилей по объектам.

Поместите число в верхнем правом углу ячейки таблицы Простои машины освобождают нижнюю половину ячейки Иллюстрация, характеризующая количество распределенных единиц Инженер. Сначала заполняется первая строка плана. Очевидно, доставка должна быть сделана следующим образом: Направление с наименьшим временем простоя, то есть A, B4.

Вот время Время простоя (обозначенное C14) составляет 3 часа. Направление задается как минимум их суммы Доступно для A}, требуется для B4, равно 7 Следовательно, достигается полное потребление этого базового оборудования, Или полное насыщение этого объекта. На рассмотрении В этом случае объект B4 полностью насыщен (подчеркивая память).

После указанной операции на базе А остаются 4 единицы, Заключите это в скобки рядом с цифрой 11. Это отдых Рекомендуется перейти непосредственно к объекту B3, так как это приведет к простою Направления A и B3 являются оставшимися минимальными значениями. Теперь все Ресурсы на основе A1 исчерпаны (A) Акцент), а для объекта B3 требуется 5 единиц (это Номер указан рядом с 9 в скобках).

Продолжите, потому что все ресурсы на основе At исчерпаны Во второй строке плана, например, повторное объяснение операций Таблица 3.3 Передний план (источник) база 1 А P (4) о P (6) Аризона 8 (3) Toed Объект В 5 5 <7 2 5 Kb 5 B2 9 (3) 7 <8 4 6 3 3 7 Bz 9 (5) 5 4 2 <5 1 5 5 B4 7 3 7 0 <9 -K2 3 «Любовь 0 -3 -4 В результате получите первый или первый план Распределение машин по объектам (Таблица 3.3).

Чтобы определить оптимальность полученного плана, Время простоя, характеризующее эффективность решаемой проблемы, Я думаю, что это более ценно, чем время Меньшее время простоя означает меньше работы. Представляем понятие возможностей. Потенциал Некоторые числа и ^ и б, каждый из-за дна, Объект, который содержит сумму запланированных ячеек, которые содержат числа.

Распределенная машина равна стоимости простоев, т. Е. «» + «4 = S (* i> 0). <334) Для ячеек без распределения эта сумма больше не Стоимость результата, т.е. uA, + uB ^ (C, D ^ 0> ・ <3 ・ 35) Планирует, что все ячейки удовлетворяют условиям (3.34) и (3.35), Это лучшее. Определить оптимальность заданного источника Планируйте, сначала рассчитайте и добавьте в таблицу. 3,3 значение Возможности базы и объекта.

Предполагая, что uA] = 0, 0 = 5; 0 = 3; -5 = -4; -3 (-4) = 7; -7 = -3; (-3) = 5. Проверьте, выполнено ли потенциальное условие Для свободных клеток. Подведите итог каждому из них Сравните соответствующие возможности базы и объекта Значение с временем простоя в правом верхнем углу Угол клетки. Общий потенциал свободных клеток Псевдо значение, обозначенное C. Они написаны слева Верхний угол ячейки.

Из уравнений (3.34) и (3.35) оптимально Версия плана: C- (λ <0. Как видно из таблицы 3.3, условие (3.34) Он выполнен для всех свободных клеток. Итак, этот план Оптимальное. Для оптимальных условий Не соблюдаю, планирую Улучшено. Пример 3.3 Предположим, что производственная компания имеет Четыре команды профессиональных работников.

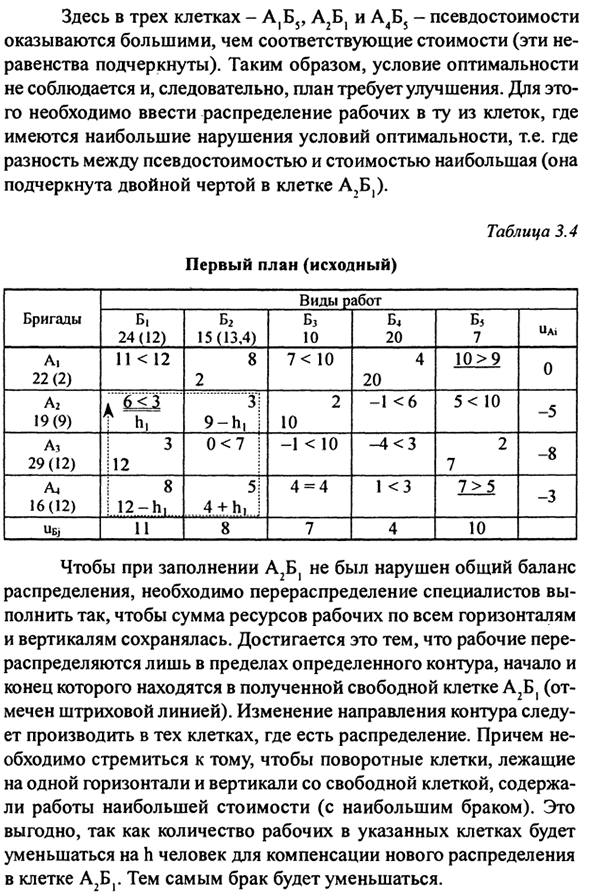
Профиль: условный А, А2, А3, А4. Специалисты для этих команд Условно распределяются по пяти различным типам работ: B, B2, B3, B4, B5. от Как работники распределяются по этим типам Прежде всего, качество продукции. При разработке конкретного плана распределения работников Эксперты подходят для математических приложений программирование Сначала составляется исходная таблица планов (таблица 3.4).

То же, что описано выше. Как значение Псевдо значение в этом случае является значением дефекта Продукты, полученные с этим распределением рабочих Тип работы. Здесь три ячейки — A, B5, A2Bj и A4B5 — псевдо значения Вы можете видеть, что они больше, чем соответствующие расходы (это Неравенства подчеркнуты). Поэтому оптимальные условия Поскольку вы не следуете, вы должны улучшить свой план.

Из них распределение работников должно быть введено в ячейку. Максимальное нарушение оптимальных условий, т. Е. Где Разница между псевдо-значением и значением является наибольшей ( Клетки A и B подчеркнуты двойными линиями). При заполнении A2Bj сохраняйте баланс всего Требуется экспертное распространение и перераспределение Сумма трудовых ресурсов во всех ракурсах И вертикаль сохранилась.

Это потому что рабочие Перераспределяется только в пределах определенного контура, Последний находится в результирующей свободной ячейке A2Bj. (Отмечено пунктирной линией). Изменить направление контура Должен быть создан в ячейке с распределением. далее Вы должны приложить усилия, чтобы убедиться, что вращающаяся ячейка лежит.

Та же горизонтальная и вертикальная, что и у свободной клетки, Самая ценная работа (включая самый большой брак) была включена. Это Количество работников в этих камерах Уменьшите на h, чтобы компенсировать новое распределение Следовательно, брак внутри клетки A B уменьшается. Чтобы сохранить общий баланс, добавьте h работников в клетку. Альтернативные дополнительные знаки в схеме A4BG.

Распределение h во вращающейся ячейке: ячейка A2Bj-plus, в ячейке A2BD-значение дополнительного количества работников, например, минус Нужно выбрать не выбирать какой-либо дистрибутив Это не стало отрицательным. В этом случае h = 9. После распределения работников на трассе, второй Запланируйте это для более разумного распределения Специалисты лучше оригинала (Таблица 3.4).

Общая стоимость брака по первому плану составила: Y1 = U £ 11 Schxc = 8 ・ 2 + 4 ・ 20 + 3 ・ 9 + 2 ・ 10 + 3 ・ 12 + я = я и + 2 · 7 + 8 · 12 + 5 · 4 = 309. После улучшения плана стоимость брака Au снизилась В зависимости от следующих значений: Ay = C21h1-cyi, + C42h, -C41h, = h1 ・ (C21-C22 + C42-C4I) = = (3-3 + 5-8) 9 = 27. Общая стоимость брака во втором плане (у2) выглядит следующим образом: y2 = y1-Au = 309-27 = 282.

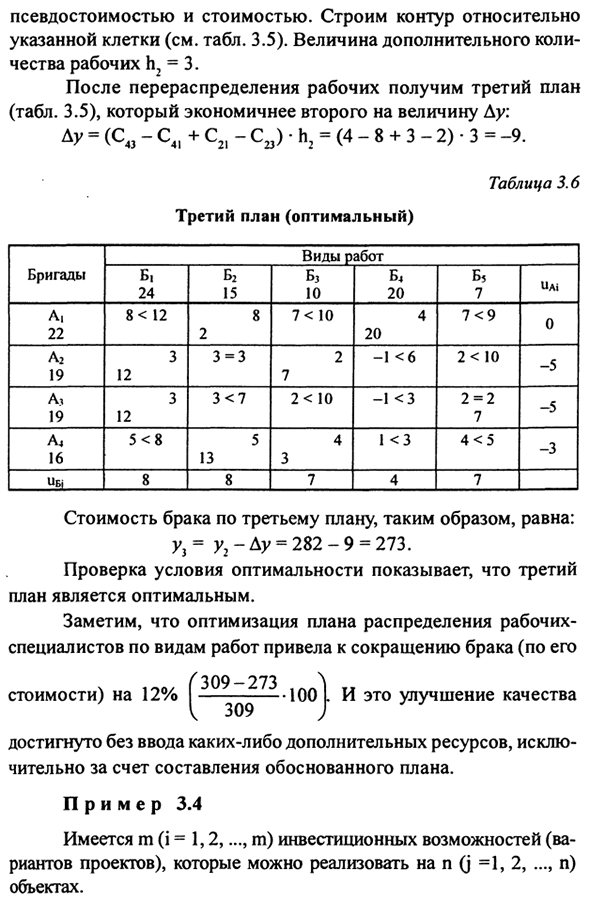
При проверке оптимальности фона Установить, что оптимальные условия не соответствуют клеткам AjB5 И A4B3, последний A4B3 Псевдо-значения и значения. Создать относительно контур Указанная ячейка (см. Вкладку 3.5). Дополнительное значение Количество работников h2 = 3. После перераспределения работников, получить третий план (Таблица 3.5), значение Au является более экономичным, чем второе: Ay = (Ce-C41 + C21-CB) -h2 = (4-8 + 3-2) -3 = -9.

Поэтому стоимость брака по третьему плану равна: у3 = у2-ау = 282-9 = 273. Проверяя оптимальные условия, План оптимален. Обратите внимание на оптимизацию планов распределения работников Работа по типу специалистов привела к уменьшению брака (его D 309-273 ^ Стоимость) 12% 100 л. И это улучшение качества Достигается без ввода дополнительных ресурсов, Просто составьте разумный план.

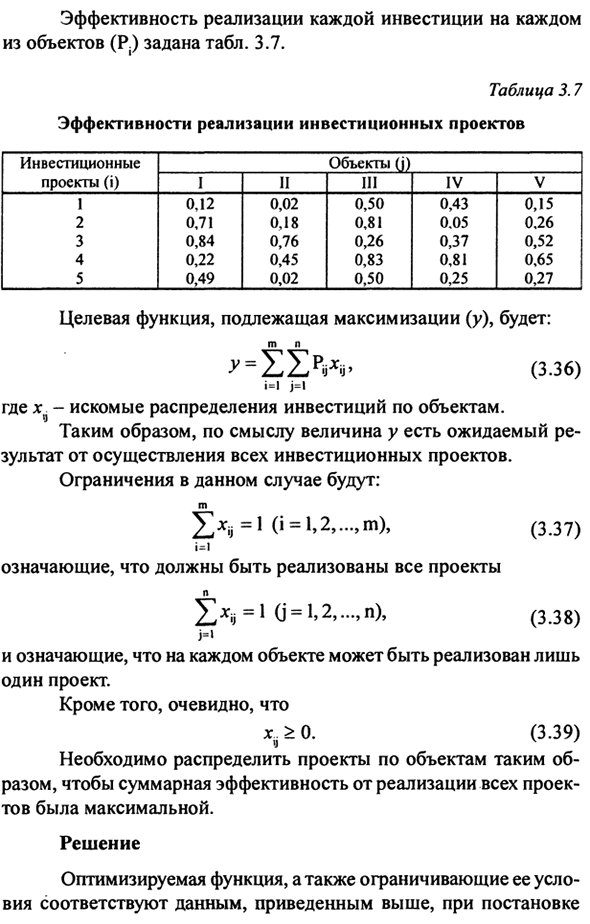
Пример 3.4 Есть m (i = 1,2, …, m) инвестиционных возможностей (Опция проекта) Может быть реализовано с помощью η (j = 1, 2, …, η) Объект. Эффективность инвестиций для каждого Таблица заданных объектов (R.). 3,7. Максимизируемая целевая функция (y) м н Y = ΣΣ? ■ ^> XH> (3,36) Где х. Желательное распределение инвестиций на объект.

Следовательно, в смысле, ожидается, что величина γ Результаты реализации всех инвестиционных проектов. Ограничения в этом случае следующие: м Σ * ϋ = 1 (i = 1, 2, …, m), (3.37) я = 1 Означает, что все проекты должны быть реализованы η Σ * ϋ = 1 0 = 12, …, η), (3.38) Это означает, что это может быть реализовано только для каждого объекта Один проект.

Кроме того, это понятно ^> 0. (3,39) Проект должен распространяться таким объектом, как Общая эффективность от всех реализаций Проект был самым большим. Решения Оптимизированные функции и ограничения И условия Соответствует приведенным выше данным при настройке Транспортное задание. Это позволяет применять метод Потенциал (слегка изменен). По аналогии с проблемой эффективности перевозок Продажи играют роль тарифов.

Все проекты Единый инвентарь груза, соответствующий каждому объекту Требуется единица нагрузки. Исходя из вышеизложенного, условия примера 3.4 представлены в следующем формате: Таблица 3.8. Сначала заполните первый план и создайте оригинальный план Прежде всего, это элемент с высокой эффективностью монтажа. начинка Начните с первой строки.

Схематическое изображение Полученный первоначальный план показан на рисунке. 3.2. На переднем плане Математическое ожидание значения равно: ух = 0,50 + 0,71 + 0,76 + 0,81 + 0,27 = 3,05. Чтобы улучшить первоначальный план с использованием потенциальных методов, Положитесь на следующие искусственные методы:

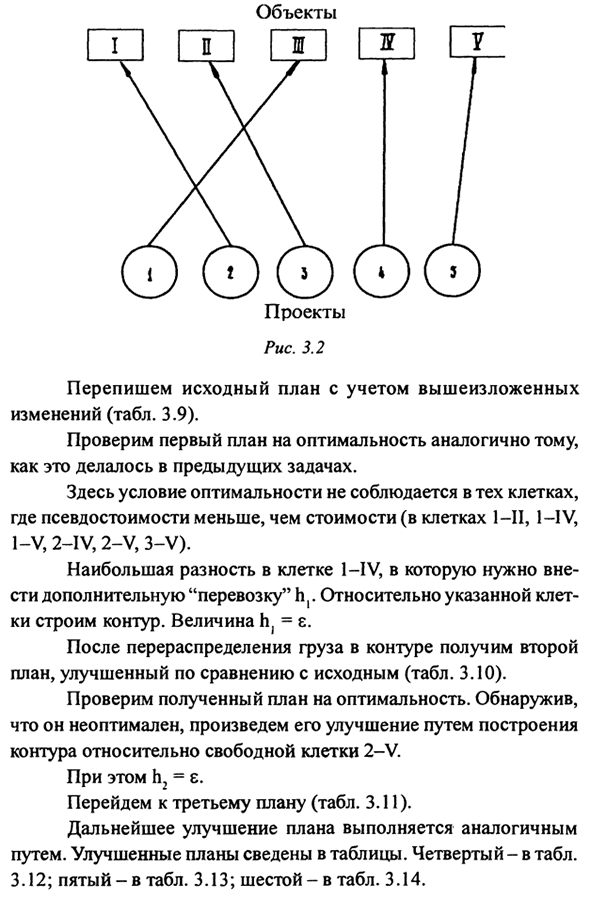
Сделайте дополнительный «транспорт». ε одновременно в каждой строке плана Планы, связанные с балансом Вертикальный и горизонтальный. Чтобы такие действия не вызывали искажения В плане величина ε считается сколь угодно малой, поэтому Не важно добавлять или исключать планы. Перепишите первоначальный план с учетом вышеизложенного Изменения (Таблица 3.9).

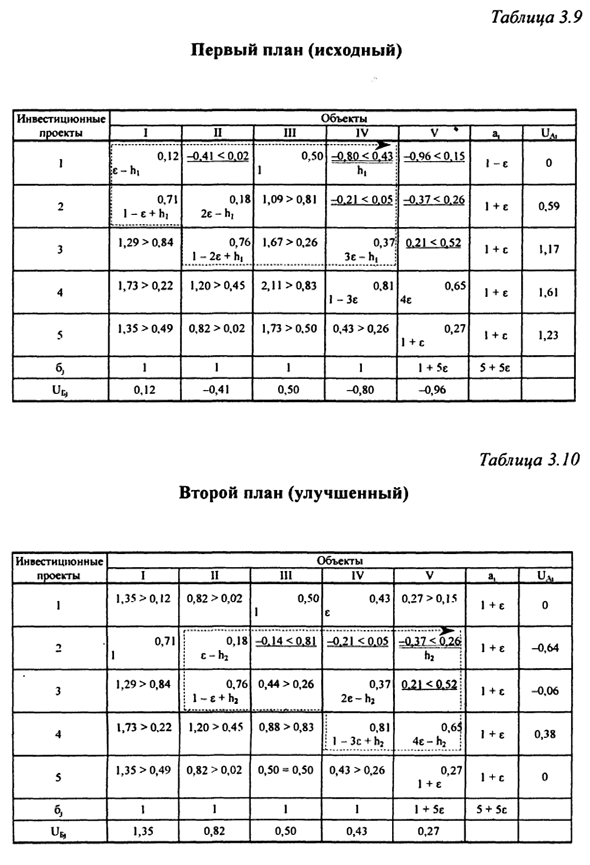
Проверьте оптимальность первого плана таким же образом Как и в предыдущем задании. Здесь оптимальных условий в этих клетках не наблюдается Где псевдо стоимость — это стоимость (ячейки 1-P, 1 — IV, 1-V, 2-IV, 2-V, 3-V). Самая большая разница в ячейке 1 — IV, Создать дополнительное время «перевозки» по сравнению с указанным Ячейка строит цепь. Количество h} = ε.

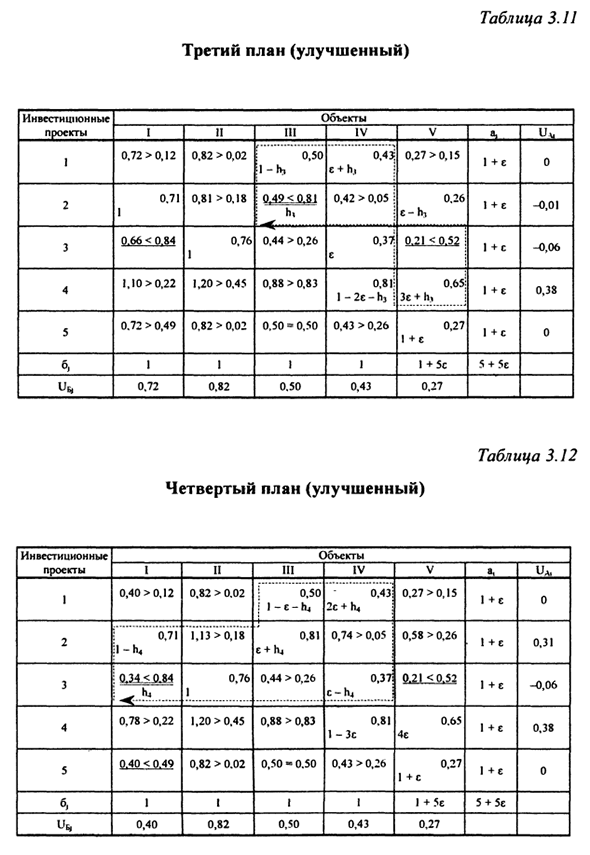
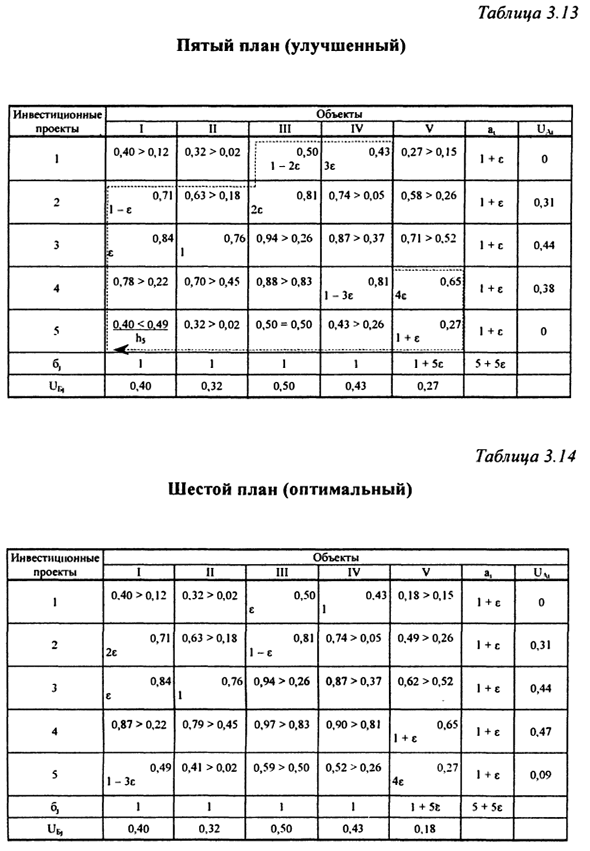
После перераспределения нагрузки в цепи, второй План был улучшен по сравнению с первоначальным планом (Таблица 3.10). Проверьте оптимальность полученного плана. Когда вы обнаружите Улучшать, строя неоптимально Относительно свободный 2-V контур клетки. Кроме того, h2 = ε. Давайте перейдем к третьему плану (Таблица 3.11). То же самое касается дальнейших улучшений в плане. Кстати. Улучшенные планы сведены в таблицу.

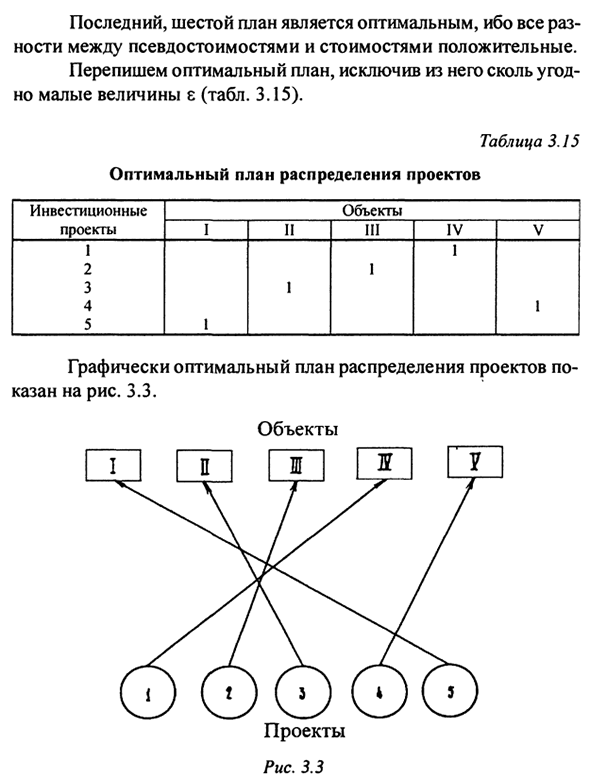
Четвертый в таблице. 3.12; 5-е место в таблице. 3,13; 6-е место в таблице. 3,14. Последний 6-й план идеально подходит для всех Разница между псевдо-значением и значением является положительной. Перепишите лучший план. Любое небольшое значение ε (Таблица 3.15). Графически оптимальный план распространения проекта Показано на рисунке. 3.3.

Смотрите также:

• Решение экономико математических методов

Сетевое планирование	Нелинейное программирование (планирование)
Логические задачи и задачи на смекалку	Динамическое программирование (планирование)