Оглавление:





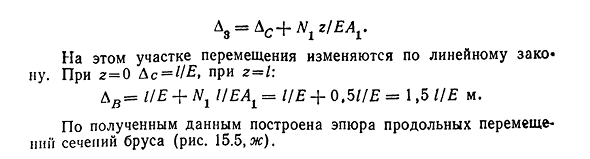

Продольные и поперечные деформации бруса при растяжении (сжатии). Закон Гука. Перемещения
- Продольная и поперечная деформация балки при растяжении (сжатии). Закон крючка. Приложим внешнюю силу F к стержню длины / постоянной площади сечения A(рис. 15.4, а). Изображая силу стрелы, как уже говорилось, она считается равномерно распределенной по всем концам. Другими словами, предположим, что все воображаемые продольные призматические элементы (волокна) балки нагружены равномерно и подвергаются одинаковой деформации. Под действием натяжения длина стержня I увеличивается на величину AZ, как показал эксперимент, Тысяча и
сто тысяч. Его поперечные размеры уменьшаются. Для риса. 15.4, и пунктирная линия показывает диаграмму деформации протянутой балки. Когда сила действует в противоположном направлении, луч сжимается. В случае сжимаемого стержня с меньшей длиной по сравнению с его поперечными размерами его длина I уменьшается на величину D/, а поперечные размеры увеличиваются.
Если длина балки значительна по сравнению с ее поперечными размерами, то сила сжатия может согнуть ее, то есть происходит потеря Людмила Фирмаль
устойчивости. Этот случай будет рассмотрен в главе 24. Величина D / называется продольным удлинением стержня при растяжении. Удлинение при растяжении считается положительным, а укорочение при сжатии-отрицательным. Естественно, что чем больше сила растяжения балки и ее длина, тем больше удлинение D/, и наоборот, и чем больше поперечное сечение, тем меньше брус из разных материалов будет удлиняться при разных значениях. Связь между мощностью и удлинением называется R. R Гука law.It впервые был получен Гуком.EAS константа Nz и Az Al-N1 / EA, (15.4), где D / —
абсолютное удлинение балки./ Это физическая постоянная материала, характеризующая его способность противостоять упругой деформации. Чем больше Е, тем меньше продольная деформация.EA-жесткость поперечного сечения балки при растяжении или сжатии. Таким образом, удлинение балки прямо пропорционально силе, действующей на поперечное сечение N и обратно пропорционально длине балки I и жесткости балки EA. Поскольку в любой точке рассматриваемой балки О2 имеет одинаковое значение, то линейная деформация 141в все точки будут одинаковыми, их значение можно определить по формуле E2=D///. (15.5) Линейная деформация при
- растяжении балки (сжатии), Е2 обычно называется растяжением или относительной продольной деформацией. Относительная продольная деформация-это абстрактная величина, равная абсолютному удлинению единицы длины балки. Если разделить левую и правую части уравнения (15.4) на I и указать a-Z=N / At, то D/ / =N / EA;E2= O2 / E или (ЮЖД = эз)(15.6) В свою очередь, закон крюка можно сформулировать следующим образом: относительная продольная деформация прямо пропорциональна соответствующему вертикальному напряжению. В то же время размеры поперечного сечения (ширина b и высота y) уменьшаются за счет продольной
деформации при растяжении стержня. Обозначает горизонтальное укорочение от B и h до-D6 и-Dy(рис. 15.4, 6). Относительная поперечная деформация экс—\б!b\EU= — &h/h. (15.7) Для изотропных материалов поперечная деформация одинакова.7. Как показывают эксперименты, при напряжении, не превышающем предела упругости, относительная поперечная деформация прямо пропорциональна относительной продольной деформации, но имеет противоположный знак: eg= — ex / p= — Ey/[i. (15.8) Отношение поперечной деформации к продольной (абсолютная амплитуда) называется коэффициентом Пуассона: И=I| / / E2|. (15.9))
Коэффициент Пуассона C является безразмерной величиной. Продольные упругие константы E и C являются физико-механическими свойствами Людмила Фирмаль
Изотропных материалов. Коэффициент Пуассона был определен экспериментально. Для различных материалов он имеет значение от нуля (для пробки) до значения, близкого к 0,5 (для резины). Для стали C составляет 0,25-0,3,для некоторых материалов значение E и C приведены в таблице. 15.1. 142T a b l I C a15. Один Имя материала E, MPa L имя материала E-M P A th Сталь 2.1-10 » 0.25-0.3 бетон (0.18-0.25) 10* 0.1— 0.2 Медь 1• 10* 0,31—0 ; 34 камень 0,01*105 0,16— 0,34 Алюминий 0.7-10″0.32-0.36 дерево 0.1 * 105-чугун 1.1-10″ 0.23-0.27 стекло 0.56 * 105 0.25 Движение поперечного сечения штанги. Изменение поперечного сечения — это изменение начального положения поперечного сечения в результате деформации балки. Движение
может быть линейным из-за изменения расстояния или угла при повороте секции. Исходя из гипотезы о плоском сечении поперечного сечения после деформации барина центральное натяжение(сжатие) занимает новое положение параллельно исходному, смещаясь вдоль оси за счет расширения (укорочения). В этом случае угловое смещение всех поперечных сечений равно нулю. Кроме того, смещение рассматриваемого участка, поскольку величина смещения представляет собой изменение расстояния между двумя участками, зависит от того, вычисляется ли смещение для какого участка, как
правило, в виде сечения, как линейное (продольное) движение балки вычисляется как сечение, сечение, где величина жесткости (перемещение равно нулю) равна Перемещение определяется выражением &=N l/E A, (15.10), где I-расстояние между исследуемыми участками, N-внутренняя продольная сила, а EA-жесткость балки при растяжении(сжатии). Если стержень между двумя исследуемыми участками имеет ступенчатое изменение поперечного сечения или нагружается каким-то внешним продольным усилием фокуса, то участок съемки будет закрыт.、 Смещение вычисляется как алгебраическая сумма расширений отдельных участков: 143). 15.5 D=5W или / E A t). i = l Результат расчета указывается в виде графика
продольного смещения сечения балки. Процесс построения графиков движений объясняется примерами. Например. Для ступенчатых балок (рис. 15.5, а) построить график движения. Решение. Для этого бара см. рис. 15.2, b, C) внутренние продольные силы уже рассчитаны и построены графики N и az, поэтому перейдем непосредственно к построению графика продольных перемещений. В этом случае ступенчатый стержень имеет три секции KD, DC и CB, в которых построены N и o^. Верхняя секция K, которая совпадает с жесткой прижимной опорой, не имеет движения, поэтому рассчитайте движение остальных секций балки против нее. Во-первых, рассмотрим сюжет KD. В любом сечении сделайте смещение от
верхнего удлинения 1-1(рис. 15.5, g) равно DX=N2z / EA2-z / E. Из этой формулы мы устанавливаем, что закон изменения смещения вдоль участка KD является линейным. 2=0DL=0; z=l=AZ / ^=0.75 TSE m. Участок постоянного тока. Перемещение любого сечения 2-2(рис. 15.5, d) равна сумме смещения сечения DK и удлинения балки на длину z сечения DC:^S D+Nt z/EA2. Закон изменения смещения также линейный. От 2=0=0.75/£’, z=l&c = QJ5l/E+Nil / EA2=0f75l / E+0.25 l / E / E-=TSE m. Любой участок 3-3 Санкт-Петербурга(рис. 15.5, д) сумма перемещений двух верхних частей KD и DC и длины балки на участке CB длиной z равна: 144А Три. =A c+^Z>E A1-в этой области смещение изменяется линейно. АТ2=0=АТ2=з:АВ=цэ+НР UEAt = цэ+0.5/ / Д=1.5 м це. По полученным данным строится график продольного смещения поперечного сечения балки (рис. 15.5, г).
Смотрите также:
Решение задач по технической механике
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

