Оглавление:




Принцип Даламбера
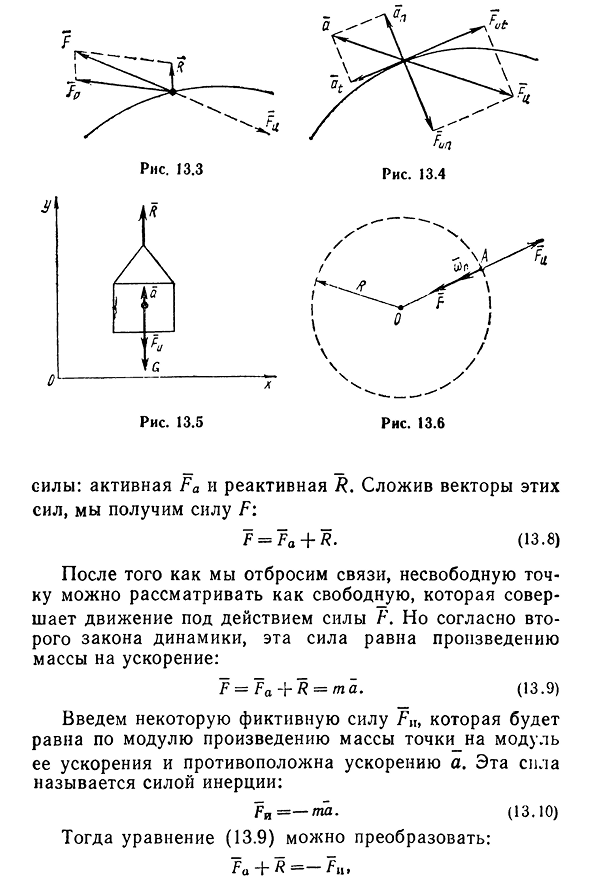
- Предположим, что принцип Даламбера состоит в том, что материальная точка А имеет массу t и движется в результате действия активной силы Fa(рис. 13.3). В общем случае материальная точка не свободна, то есть ее движение затруднено различными связями, через которые возникает сила реакции. Если мы уберем
связь и заменим ее действие реактивной силой, то они будут действовать в точке А 117). Рис. 13.5. 13.6 Если вы добавите вектор этих EIL, вы получите силу F: F=Fa+R.(13,8) Однако, согласно второму закону динамики, эта сила равна произведению
массы за счет ускорения: Ф=(13.9) Введем некоторую мнимую силу Fn, модуль Людмила Фирмаль
ускорения которой равен величине на весе Токина и противоположен ускорению A. Эта сила называется силой инерции: RA= = — hPa. (13.10)) Затем вы можете преобразовать уравнение (13.9: Fa+R= — F Ut 118. F+tf+FM = O. (13.1!) Это уравнение выражает принцип Германа-Эйлера-
Д’Аламбера-несбалансированная система сил, приложенных к движущейся материальной точке, может быть уравновешена силой инерции. В будущем этот принцип будет называться принципом Даламбера. Согласно формуле (13.10), сила инерции возникает только при движении с ускорением. В случае криволинейного и
- неоднородного движения полное ускорение материальной точки можно разложить на касательное и вертикальное ускорения. Итак, сила инерции — это тангенциальная сила нормальной силы инерции Fnn и силы инерции Fttt(рис. 13.4 определяется по формуле)、 Рин-т а п»(13.12) КЛ = — мат. (13.13)модуль представляет собой полную инерционную силу F1=V F2+F2/. AI V IP «‘ I/(13.14) как уже упоминалось, сила инерции является фиктивной. Однако с помощью принципа Даламбера неуравновешенная система может быть
преобразована в уравновешенную систему, и в такой системе необходимо соблюдать закон статики. В динамике 1) определение силы, действующей на тело по известным законам движения точек;2)определение закона движения материальных точек по известным силам, действующим на эту точку. Вторая проблема-обратная первой. Давайте рассмотрим, как решить эти задачи, используя принцип Даламбера. Например. Стеновая панель массой G разгоняется линейно и равномерно с ускорением а краном (рис.13.5). Определите натяжение кабеля. Решение. Когда панель движется вперед, все точки имеют одинаковую скорость и ускорение.
Поэтому его можно считать важным моментом. Замените кабель, Людмила Фирмаль
реагирующий на операцию R. В соответствии с принципом Даламбера, панель Действует сила инерции 119fh=ma, но m=G!Тогда Ф=а=(Глг) есть. Составим уравнение равновесия по оси y: R-Fn-G=0, R=F»+G=(Ga)/g+G=G(1+a/g). Например. Материальная точка А имеет массу/I, равномерно вращающуюся вокруг точки о(рис. 13.6). Натяжение нити с силой, с которой точка соединена с центром вращения, равно F. Решение. Поскольку материальная точка имеет равномерное вращательное движение, тангенциальное ускорение равно нулю, а нормальное ускорение-методу an-v2IR. Итак, если рассматривать точку материи как свободную, то на нее влияет реакция нити накала F, а согласно принципу Д’Аламбера, сила инерции Fn=anm. Из уравнений равновесия на оси через центр вращения и точку L вещества получаем F^ — F=0 или anm-F-0. __ Скорость вращения v=] FR=FR / m.
Смотрите также:
Решение задач по технической механике
| Основные положения динамики. Законы динамики | Работа переменной силы на криволинейном пути |
| Методика решения задач | Поступательное движение твердого тела |
Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.

