Оглавление:



















Первый закон термодинамики
- В своей практической деятельности человек сталкивается с различными процессами природы и техники, связанная с преобразованием одного вида энергии в другой. Как вы знаете, Энна!№. Не потому что нечего исчезать, а только переходить из одного формата в другой. В 1842 году Р. Майер установил эквивалентность тепловой и механической работы независимо от личности. Процесс преобразования энергии.
Пусть термодинамическая система учета массы WJ для объема K при температуре T и давлении P(рис. 1.5).От внешней среды(внешнего источника тепла) Когда термодинамическая система снабжается бесконечно малым количеством тепла (dQ), температура системы повышается только (dT) при определенных условиях conditions. An повышение температуры означает увеличение кинетической энергии ЕК теплового движения системы в ДЭК.
В зависимости от пары независимых переменных, Y является. Людмила Фирмаль
Согласно формуле (1.4), увеличение температуры при постоянном давлении во внешней среде приводит к увеличению. системный том мимо dV. In в этом случае часть тепла расходуется на работу разделения (сепарации) молекул, преодолевая силы межмолекулярного сцепления. По мере увеличения расстояния между молекулами потенциальная энергия системы увеличивается dE».
Общее изменение движения системы dEK и потенциальной энергии Изменение внутренней энергии dU = dEK +dEₙ. (1.28) внутренняя энергия системы является определенной функцией от 2 параметров (3 из них) рабочего fluid. So … } 1L (u, T);>(129) хотя U = A (p, П) термодинамика не определяет абсолютное значение внутренней энергии、 Рассмотрим только изменения. Изменение U не зависит от промежуточного состояния рабочего органа, а определяется только начальным и конечным состоянием системы; следовательно, 2 AL’ = Дсор =u₂-Gj.
(130) 1 если начальное состояние совпадает с конечным состоянием (см. Рисунок 1.4), jdU =0.(131) Ди |) Значение (1.29), приобретенное (132) (133) (134) изменение внутренней энергии Если температура термодинамической системы повышается, то это положительное значение.
В идеале (фундаментальные силы межмолекулярной агрегации не являются considered. In это соединение, dE » — 0 и dQ Рисунок 13.Схема определения работы при расширении рабочей температуры внутренняя энергия системы изменяется только по температуре. Тогда для идеального газа 1 кг При подаче тепла dQ в термодинамическую систему работа осуществляется не только за счет изменения внутренней энергии рабочего, но и в результате расширения объема системы R.
Величина dv при преодолении силы внешнего сопротивления(см. рис. 1.5). для определения этой работы необходимо знать площадь а поверхности, которая будет границей термодинамической системы. Масса m, на которую действует внешнее давление pa. когда температура повышается на dT, газ расширяется до минимума, и каждая точка в ограниченной области перемещается в бесконечность Короткое дальности DH. Основная работа dL = p ^ Adh-объемное изменение или механическая работа.
Поскольку основное изменение объема-Adh = dV, если pt = p (процесс расширения Равновесие) dL = pdV (137) деление левой и правой частей уравнения (137) на m дает специфическую для элемента работу dl = pdv. // Основная операция Если объем изменяется на dv, то он численно равен основной площади процесса, например, ID2 (см. Рисунок 1.4).Последняя часть l =(1.38)₽ / где t’i и 1 ′ 2 — Удельные объемы начального и конечного, respectively. In по координатам r, p этот объем работ характеризуется площадью под процесс, например, alD2h(рисунок 1.4).
Для подсчета Вам нужно знать интегральную(1.38) зависимость функции p-/®. Термодинамический процесс, такой как ID2.So, работа 1 ^(1) является функцией процесса. За счет увеличения объема термодинамической системы достигается активная работа. Потому что количество тепла, поступающего в систему, dQ, как правило, приводит к внутренним изменениям、 Энергия системы основана на законе сохранения энергии и внешней работе dL (прежде всего, закон термодинамики изолированной системы) dQ = dU + dL и dq = du + dl. (139) от Полученное уравнение означает, что при отсутствии теплоснабжения (dQ = 0) внешние работы могут выполняться только за счет внутренней энергии системы.
Формула (1.39) также имеет вид、 Подвод тепла к термодинамической системе определяется термодинамической process. In дело в том, что если изменение ду определяется только разницей между конечным состоянием и начальным состоянием. И затем… Внешняя работа зависит от свойств thermodynamics. In открытая система, внешний ECU движения и внешний потенциал Ep могут изменить должное к входному сигналу жары. Энергия рабочего тела системы= 0.5 s /(nnv2); dEₙ.w= d(gmh (1.40), где а-скорость рабочего тела, g-ускорение свободного падения, а / 1-Изменение уровня центра инерции Рабочая жидкость.
Это особенно заметно, когда рабочая жидкость движется, например, по движущемуся каналу между лопатками турбины. Внешняя работа dL в этом случае тратится на работу DB * техническая работа со смещением рабочей жидкости по каналу dL d>.Смещение самого канала в пространстве под действием силы. Перпендикулярно стенкам канала. Следовательно, видимое Движение рабочей жидкости в открытой системе dL = dLM +dLᵢₙ. (1.41)учитывая вышесказанное, первый закон термодинамики открытой системы может быть выражен уравнением dQ-D. U + 0.5 J (mw2)+ d (gmh)+ dL, K 4-dL, ₙ (142) и (1.40) и (1.41) рассмотрим dQ = dU + dE ^ M + w + dL (1.43) в изолированной системе подача энергии не изменяется.
За счет уменьшения внутренней энергии работа может быть завершена только в неравновесных процессах (механических, тепловых, химических, ядерных).Не позволять Тело обладает определенной внутренней энергией, например, для получения работы от тела, находящегося в состоянии температурного равновесия. Поэтому его невозможно создать Первая роль вечный двигатель, который работает без внешнего источника энергии, и 2-й вид вечного двигателя、 Тепловое равновесие.
Если тепло подается в термодинамическую систему в течение определенного интервала термодинамического процесса, то уравнения(1.39) и (1.42) Нужно сделать инъекцию. Q = AU + 0.5 m (w ^ — wi)+ gm(h₂-hi)+ 4-U + trcK(144)и Q = AU + L(1.45) или q = Au + 0.5 (w ^ — ВФ)+ \ + г (h₂ -,.)+ / Ю. К. 4 — / Tcₓ; ? (1.46) м = ам + И. рис. 1.6. Тепловой процесс LT регулирует энтропию, энтальпию и энтропию теплоемкости. Работа определена Интеграл (1.38) выполняется рабочим телом термодинамической системы только при изменении объема. Давление может быть функционально зависимым остается постоянным. По объему.
Однако, если p = 0.? = 0, если изменяется громкость. Эта работа представляет собой своеобразный энергетический обмен между термодинамической системой и окружающей средой. Энергетический обмен может Q генерируется в виде определенного количества теплопередачи. Значение q, Как и/, может быть вычислено в виде интеграла, форма которого совпадает с Интегралом (1.38).И действительно Давление определяет возможность выполнения работы, а температура является очевидным признаком возможности передачи энергии в виде тепла.
Однако, даже если температура (давление) измеряется Вы можете определить количество тепла, которое передается в любое время. Например, если в кипящую воду подается тепло, ее температура не меняется до тех пор, пока она полностью не вскипит (см. область / 7, Рис.1.3). Как и в случае с объемом при выполнении работ, был предложен параметр, изменяющийся только на величину передаваемого тепла(при dv> 0 работа положительна, а при dv 0-отрицательна). 1852 Р. Клаузиус и затем С. энтропия, которую называют энтропией, не может быть измерена таким методом, как объем, она определяется только calculation. By аналогия .
Для Интеграла (1.38), количество тепла Si Q = f TdS s, или dQ = TdS. (1.47) (1-48) dS> 0, который поставляет тепло в термодинамическую систему. dS 0-присваивается. Специфический Количество теплоты ’ 2 q — $ Tds и dq = Tds, (1.49) h, где s-коэффициент энтропии. Для вычисления Q или q требуется функционально-зависимый T = f(5). Для определения объема работ необходима зависимость p-f (v) (см. Рисунок 1.4).Определены зависимости функций T = f (s) и p — /©!Термодинамический процесс, следовательно термодинамический Широко используются координаты vp, характеризующие выполняемую работу (см. рис. 1.4), а также координаты 5 T, характеризующие теплообмен с внешней средой (рис.1.6).
Под областью Процесс 12 соответствует интегралу (1.49) и характеризует количество подводимого тепла в случае, когда s увеличивается (ds> 0) и s уменьшается (ds 0). 0).Энтальпия. Энтальпии I =и+ pv часто используются в термодинамических расчетах. (1.50) для внутренней энергии u определяется давление p и удельный объем v Состояние термодинамической системы, энтальпия I, является функцией состояния. Внутренняя энергия идеального газа[опорные уравнения (1.35) и (1.36)] и следующий продукт pv .
Поскольку уравнение состояния (1.4)зависит только от температуры, то энтальпия I =(1.51) позволяет оценить изменение энтальпии при изменении состояния В термодинамической системе необходимо различать уравнение (1.50): di = du + p du + vdp. Если сравнить его с формулами (1.39) и (1.37), то получим: di = dq + vdp (1.52). Или рассмотрим (1.49) di = Tds + vdp. (1.53) уравнения(1.52)и (1.53) являются 2-мя формами, описывающими первый закон термодинамики. Теплоемкость определяется следующим образом Отношение c = dq / dTb(1.54) откуда dq = cdT или q f f cdT. (1.55) г, теплоемкость зависит от характера термодинамического процесса.
Или, следовательно, при экспериментальном определении всех величин тепло удаляется.2 термодинамические процессы (теплоемкость ck), которые обычно протекают в постоянном объеме, и Давление (удельная теплоемкость cp).Теплоемкости различных материалов (si и cf)суммируются в таблице. в случае дл-0, тепло подается на определенное количество、 Изменение внутренней энергии du (1.39). при постоянном давлении температура рабочего тела изменяется на 1 к, так как определенное количество тепла также используется для завершения работы. P = const — это cp> >, потому что он требует большего количества тепла, чем v = const.
В зависимости от способа определения количества рабочей жидкости, теплоемкость составляет Конкретных[CF и Си Дж /(кг * K)], объем[г р и S, Купянск, Дж /(m3K)] и молярная [КСО и КРУ, JDmol * к)].Все они связаны между собой отношением к P = » £p / \ l. cp = re и / p; (1.56) 4 = pcr / 22.4; & = Kk / 22.4; (1.57) s’R » rsr; eV = rei,(1-588) где q-молярная масса рабочего тела. p-это плотность. Идеального газа теплоемкости СР и CK являются независимыми Это четкая функция температуры, как от объема, так и от давления.
Теплоемкости cf и cc различных веществ различны и зависят от температуры. Иногда это грубый расчет Температурная зависимость игнорируется, теплоемкость остается постоянной. Тогда, согласно формуле (1.55), Qp = tcp(T2-7 ’1)или Ck = wuv(7′ 2-Л). (1.59) Теплоемкость — это количество тепла, необходимое вашему организму для нагрева до 1 градуса (1°C или 1K).в большинстве случаев следует учитывать функцию c = f (T Он используется для определения количества подаваемого тепла или removed. It численно равна площади под характеристикой процесса 12 (рис.1.7).
Вы можете увидеть количество тепла. При использовании среднего значения удельной теплоемкости Op при V = const или p = const, оно определяется отношением A к » P I = //(Т₂-7). (1.60) g. In этот случай, область a12b Равная площади а34в. ССР позволяет рассчитать количество подводимого или отводимого тепла с помощью такой формулы, как (1.59). таблица средней теплоемкости при P = const и v = константа обычно находится в диапазоне температур 273 к-ТГ. Если необходимо получить количество подводимого тепла в диапазоне температур 7’1-Т₂, определите G.
B = Op(T, −273); q₂= nc>(Т₂-273),271к27. 3К, ПЬТ, Q-SPH (Т₂-273)-(г,-273). D, 273 K 273 K (161) во многих случаях В теплотехнических расчетах зависимость c = f (T)линейна, поэтому c = a + bt, (1.62) где t-температура°C. Если ξ= 0, то c-a (α t-0°C); b-dc / dt-наклон прямой линии (1,62). в этом случае3 q = J (а+ bt) dt = [a + 0,5 b(t₂+11)] (t₂-ГД » где I, средняя теплоемкость диапазона температур H — /serser = a +О.5Ь (₂+Г1).(1.63) * 1 рисунок 1.7.Температурная зависимость теплоемкости когда рабочим телом является смесь газов, удельная теплоемкость составляет» .
Смесь и k-lk k = «» =£gSk или c; =£r * 4. (1.64)* -> k = 1 выражение (1.39), принимая во внимание (1.37), все тепло при v = const Потрачено на изменение внутреннего energy. So мы учитываем (1.55) с v = const dU = CydT. (1.65) сравнить с Формулой (1.36) и попасть внутрь Поскольку энергия зависит только от температуры, формулы(1.65)и(1.66) справедливы и для других термодинамических процессов. в процессе Р = const、 Формула (1.39) cₚdT= CvdT + pdv pdv = RdT, поэтому уравнение идеального газа Мейера является Cp-Su-R. (1.67) умножьте уравнение (1.67) на молярную массу、 Учитывая соотношение(1.6), picₚ-ПУ? Р = 83.14 kJJkmol * к).
Из уравнения (1.68) (1.52), dq = di-vdp. (1.69) если dp-0 для p = const, dqn = cₚdT и DI =cₚdT. Поскольку энтальпия (1.70) зависит только от температуры, формула(1.70) справедлива и для других термодинамических процессов. Вышеприведенное уравнение (1.67) заполняется, когда идеальный газ принимается в качестве рабочего тела в равновесии process. In случай рабочего процесса в реальном рабочем органе, формула(1.39) Принимая во внимание формулу (1.49), ее можно выразить как Tds ^ du + pdv. Формула (1-7 TL » (//Т ⁺ [(Эг ⁺ р ?Или счет (1.66), процесс идет.
Поток при постоянном давлении, Tds = dq» =cₚdT и[Я. ’■’=>Выражение энергии @т ⁺ р / арактеризирует тепло, затрачиваемое на фиксацию Внутренние Р » чего-изменения в организме, обусловленные изменением работы J и объема. Для идеального газа выполняется условие (1.35), поэтому он следует формуле (1.4). (^) п = «/ р — 0-73) учитывает условия (1.35) и (1.73) формулы (1.72) и получает формулу (1.67).Термодинамический процесс идеальных газов и паров Необходимо выявить равновесные и обратимые термодинамические процессы идеального газа.
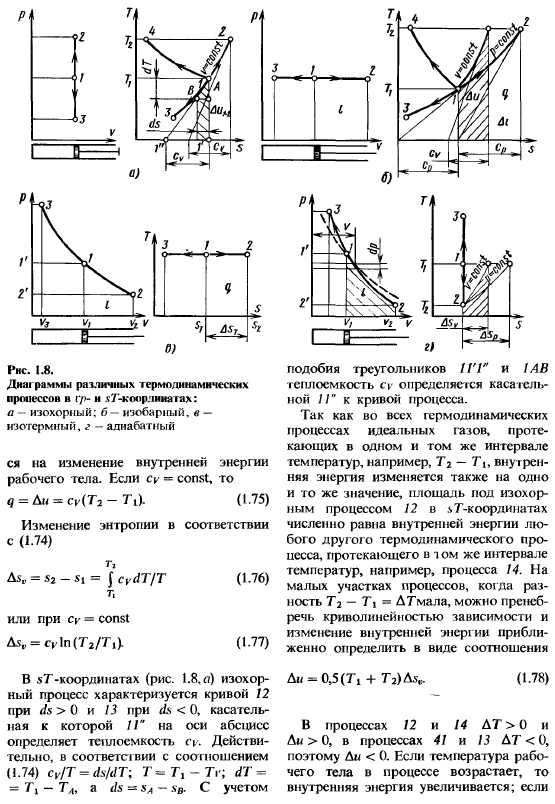
Во-первых, закономерность изменения основных параметров, характеризующих состояние работников Во-вторых, особенности реализации условий первого закона thermodynamics. In в общем случае, 2 параметра рабочего тела могут быть изменены произвольно. Но наибольший интерес Представляет некоторые особые случаи. Некоторые термодинамические процессы включают следующее: изотермический (dT = 0); термоизоляция (dq = 0) и При определенных условиях образуется политроп, который можно считать обобщенным по отношению ко всем вышеописанным термодинамическим процессам. Изопластический процесс(рисунок 1.8, а) / по уравнению состояния (1.4)?
Он записывается в формате / C = p / T = const. In изометрический процесс, давление газа пропорционально температуре и работа[опорное уравнение (1.37)] является Совершено (dv-0).Из уравнения первого закона термодинамики (1.39) рассмотрим соотношение (1.49): dq = Tds = du =cᵥdT, то есть (1.74), то есть все подводимое тепло Процесс потребления I30horn-это процесс, который происходит в физической системе с определенным объемом.
РНС. 1.8.At в нижней части рамки находятся различные термодинамические процессы c — > n l7′ — coorlia gach. а-изометрические: б-изобарные, в-изотермические, д-адиабатические изменения внутренней энергии рабочего тела. для Су = const и М =и U = ТИЦ(T₂-ти). (1.75) изменение (1.74) R> как.. = = $ CydT / T(1.76) T |или если Cy = const M=cᵣln (T₂/ n). (1.77) в координатах sT (Рис.1.8 а) изоморфный процесс характеризуется касательными, где// *горизонтальной оси определяет удельную теплоту s, ds> 0 для кривой 12, ds <0 для кривой 13.Конечно, согласно В соотношении (1.74), Su / T = ds / dT’, T ^ Tg-Tg; dT = = 1 \ — T> a ds = * sA-sB.
Принимая во внимание подобие треугольника 1GG и 1AB, теплоемкость cy является касательной кривой процесса!- Определяется по 1G. Во всех термодинамических процессах идеализированного тела, протекающего в одном и том же температурном диапазоне, например, Т₂-7\, внутренняя энергия также изменяется на одинаковую. Значение, 12-Я область при изопластическом процессе. Координата $ T численно равна внутренней энергии других термодинамических процессов, протекающих в i-м диапазоне температур.
Например, процесс 14.In в случае разности Т₂-Т \ = Дтmala в небольшой части процесса криволинейностью зависимости можно пренебречь, а изменением внутренней энергии примерно Отношение Di = 0,5 (Ti +T₂) в виде faᵥ. (1.78) в процессах 12 и 14, DT> 0 и Di> 0, в процессах 41 и 13, DT <0 и, следовательно, Di <0.Если температура рабочей жидкости в процессе повышается、 Тогда внутренняя энергия будет increase. As температура снижается, внутренняя энергия уменьшается. Изобарный процесс (рис. 1.8.6) описывается в v / T форме уравнением состояния (1.4- R / p = const следовательно, объем пропорционален температуре.
P = const по формуле (1.38) для обработки 1 кг газа/ =(pdv = p (v₂-пД (1.79)» I в PR-координатах Работа I численно равна площади процесса 12.для dv> 0 (r₂> Vi) работа положительна. Учитывая выражение (1.4), выражение (1.79) равно/ = Из I (72-7E(1.80) отношение (1.70), если p-const, то dq = di, а если cp = const T\, Asₚ>0.Таким образом, в sT-координате изобарный процесс 12 прогрессирует、 При увеличении T энтропия возрастает. Если тангенс процесса изометрии по оси абсцисс определяет то же самое, то тангенс изостатического процесса по оси абсцисс равен $ Т-коор-dipatah определяет КВС. cₚ>coincoinacuo(1.67), поэтому изобары в координате sT являются изолиниями.
Из соотношения (1.83) следует, что площадь изобарного процесса равна 12 координаты sT численно равны изменению энтальпии AI. In в термодинамическом процессе мы считаем, что изменение энтальпии определяется только изменением температуры.、 Если это происходит в том же диапазоне температур, изменение энтальпии такое же. Поэтому площадь под изобарным процессом в координатах St диапазона температур численно равна.
Изменение энтальпии в других термодинамических процессах, происходящих в том же диапазоне температур, например в процессе 14.In небольшая площадь процесса, разница т-7 | = DT мала, кривизна линии пренебрежимо мала, а изменение энтальпии можно определить приблизительно из соотношения 61 = 0,5 (7,+ Ti)^ (1,85). в процессе 14 температура Следовательно, Ai] 4> 0.Если во время процесса температура рабочей жидкости снижается, то энтальпия д1<0.Изотермический процесс (рис. 1.8, в) описывается уравнением состояния (1.4).
Изобарный процесс-это процесс, происходящий в физической системе при постоянном внешнем давлении. Изотермический процесс-это процесс, происходящий в определенной физической системе Температура. Pr / Pi = vi / v2, то есть давление и объем рабочей жидкости обратно пропорциональны. поскольку dT = 0, из формул (1.65) и (1.70) внутренняя энергия и энтальпия равны Изотермический процесс остается тем же самым.
Тепло, подаваемое рабочим, расходуется на работу: l = q = J pdv-J RTdv / v = RT \ n(v2 / i’I)»». (1.86) или/ = 47 = PlD / ln(v₂ / t’I) = Pl’llln (pi / p2). (1-87) в соответствии с Формулой (1.49) (/=T (s₂-i)= AsrT. Изменение энтропии Д$ r = $ — «1 = R In(t’ / t> i)= R In (pi / p₂). (1.88) теплоемкость изотермического процесса по формуле (1.54) Cp =±co. Процесс изоляции (рисунок 1.8.?Что это?、 Работа [опорная формула (1.39) J может быть выполнена только за счет внутренней энергии, то есть di = — du. (1.89) если вы присваиваете уравнение (1.37) и (1.65) уравнению (1.39), то dq = O cvdT +pdv = 0 или (1.67) и (1.82) vdp + k pdv = 0, поскольку после дифференцирования уравнения (1.4) .
R r / (r-l). (1.96), следовательно,/ = (P1G1-p₂g₂)/(а-1); (1.97)/ = pU1 (1-7 ‘/ Т1)/(к-1); (1.98)/ = Пиви [1-(у /Ноттингем, ng1] Л * — О;(1 99)/ = РИ'[1 — (Р₂ / р1)*», 1/*⁾-1-1) координаты в (1 /100 100)/ Пол характеризуется зоной процесса.В процессе, 12 ДГ> 0, следовательно,/> 0;в процессе 13 ДГ <0, следовательно,/ <0.Согласно формуле процесса изоляции(1.49) и(1.54) Теплоемкость равна нулю, а энтропия постоянна (рис. 1.8?).в связи с этим процесс теплоизоляции часто называют isentropic.
- To определите изменение внутренней энергии. В координатах sT от энтальпии процесса теплоизоляции, например 12, точка 2 в интервале температур 7i-Т₂, проведенная равновеликими площадными линиями и изобарными линиями, определяется под «площадью».」 Формулы (1.78) и (1.85)].В физической системе происходит снижение температуры рабочего тела в процессе протермоизоляции. Физическая система не получает тепла извне и не рассеивается. Нет теплообмена между рабочей жидкостью и внешней средой. В процессе, значения внутренней энергии и уменьшением энтальпии.
Политронный процесс характеризуется одинаковым процентом количества Входное тепло, которое расходуется на изменение внутренней энергии системы. пусть c — теплоемкость политропного процесса; затем, используя формулы (1.55), (1.65) и(1.37、 Формула (с-crfdT-pdv. Уравнение (1.90) после ряда преобразований, учитывающих (с-cp) уравнение Первого Закона термодинамики вида pdv 4-(с-Ci) vdp-0 (1.39) Политроп pv » = const.(1.101) где индекс политропа » =(s-cp)/(s-cD (1.12) согласно уравнению (1.101), процесс политропа является Термодинамический процесс, который изменяет параметры состояния рабочего fluid. In при этом в течение всего процесса политропный индикатор может иметь любое числовое значение. + ко, остаются неизменными.
Следующее соотношение является допустимым: Р2/Р1. Людмила Фирмаль
Политронный процесс обобщен относительно рассмотренного ранее process. In фактически, уравнение (1.101)эквивалентно уравнению равенства (in = const), l = ±co, если u = 0, то равенство (1.101) представляет собой изобары (p = const). при n = 1 она является изотермической, а при n = k-термической insulation. By аналогия с формулой (1.92)-(1.94) =(ви / Вий; ^- (в^Г1;T₂/ ти =(p₂/ Пи)〜ⁿ—(1.103)(1.104)(1.105)рис. 1.9. n * ln показать многочлены от n Процесс политропы может быть определен по формуле к = N (1.96)-(1.1 (х)).
По формуле (1.102, вы можете найти удельную теплоемкость с =cₖ (Н-В)/(Н-1) для политропного процесса. (1.106) поэтому Таким образом, еще раз подтверждается, что теплоемкость идеального газа зависит от характера термодинамического процесса (рис.1.9). для координат vp и x ^(рис. 1.10)、 Рисуя из любой точки/и всех рассмотренных выше термодинамических процессов, все поле диаграммы, построенной таким образом, делится на 8 областей I〜VIII. Она характеризуется определенными признаками. Поэтому все процессы в левой части точки 1 на диаграмме ТП сопровождаются отрицательной работой. все процессы справа от точки 1 на схеме sT .
Происходит при подаче тепла с левой стороны-отвод тепла(подъем от изотермы с увеличением внутренней энергии и энтальпии, снижение с уменьшением) и др. Области, отмеченные розовым цветом цвет на диаграмме bp соответствует процессу, который включает ввод тепла, а Политронный процесс-это термодинамический процесс, который изменяет состояние физической системы. Поддерживает постоянную теплоемкость на протяжении всего процесса. I <0 ^ — — — ►l> 0 рисунок 1.10. (Pn ^ ’ /’ — диаграмма связывания различных термодинамических процессов по координатам .
На рисунке, например, теплоемкость положительная process. To определить изменение энтропии в политропном процессе, подставив формулу (1.54) В формулу (1.106、 Учитывая (1.49) ds * = Cyn-kn — > Tm ’после интегрирования n-Jc, Tn ^» > = e «7T | nTG — (1.107) (1.108) учитывая уравнение (1.104) и (1.105)» 1 = O ’(и〜 / с)ЛН (Би /v₂); (1.109)s₂〜»1 =(с»А0 («- М1п(р₂/Р1).(1.110) изменения внутренней энергии и энтальпии политропного процесса 12 (рис.1.11) определяются координатами^. При изотермических 2a и изобарных 2b процессах, соответственно, одинаковый температурный диапазон Т₂-area\площадь occurring. In небольшая площадь процесса, если разница между Т₂-Ti = ат невелика.
Кривизной линии можно пренебречь. Вы можете использовать формулы (1.78) и (1.85) для определения приближения an и Ai. Количество тепла в прямой части составляет 12 ^ = 0,5(T,+ T₂) Какₗ₂. (1.11) тепло удаляется из рабочего тела за счет уменьшения энтропии процесса (dq <0). Вы можете определить поведение/из диаграммы^.В соответствии с Выражение (1.46) / = Q-hell. So, грубо говоря, если разность Т₂-TJ = ат мала, то зависимость может быть линейной и/ или = 0,5 (Ti + 7i) (as₁₂+ as.). В процессе (1.112) 12 дней / <0, по мере уменьшения громкости.
Иногда политропный процесс определяется зависимостью p = / (y) и необходимо определить политропный индекс. Для этого выберите 2 пункта Процесс: p ^ =p₂ b₂, whice Рисунок 1. 11.Политропный процесс 3D рисунок 1.12. ЛТ-Диа! Рамки для определения параметров рабочего тела и других величин с помощью графического анализа n = log (P1 / P2) / log(12 / L’l). (1.1 13) Вы можете использовать зависимости в координате$ 7 (рисунок 1.11).Формула с использованием формул (1.49) и(1.65) (1.39) имеет вид ds = Учитывая ТИЦ (ДТ / т) + (р / т) ДВ или (1.4), ДС = ц ^ ц / Т)+ Р(ДВ / в).
После интегрирования s₂ — «1 =cᵣln(7′ / 7) + J? ЛН (v₂/ ви). (1.114) формула(1.53) и (1.70), дать ДС〜cₚ (ДТ / Т)-Р (ДП / п). 52-5 после интеграции! =С,1п(Т₂/Т1)+ Р в (Р₁/р₂). Если взять Т₂ = Т \ in (1.115) выражения (1.114) и (1.115), то получим выражение для определения изменения энтропии вдоль линии. T = isochores = = const и 1₂= const As ^ = RIn (v₂ / vi) (1.116), а const между Изобарой pi = const и p₂= const A ^ _-«ln (P/ P;). (1.117) формулы Используя (1.116) и (1.117), можно определить политропный индекс по формуле (1.113). фактически, n«As ^ / Asr. Ax ^ =Дх₁₂ + длр, а AH £ * ’ = asₜ₂ + avᵥ(рисунок 1.11), n =(Asᵢ₂ + ASₚ) 4asi₂ + as J(1.118) признаки изменения давления в процессе, если AP = PR-Pi и объем AR = v₂ V V-V] одинаковы (точки A и B находятся напротив линии .
Процесс 12), знак политропного индикатора отрицательный; если знак Ap и Av различны (точки A и B находятся на одной стороне технологической линии 1.11, как показано на рисунке 1.11), знак отрицательный. Скорость политропа будет положительной. Поэтому, используя sT-лиграммы, можно очень легко изучать термодинамические процессы. О полях в такой схеме(рис. 1.12) Изобары (p = const), изолинии (v = const), изотермы (горизонтальные) и изоляция (вертикальные) являются constructed. In в соответствии с формулами (1.116) и (1.117) изобары и изолинии находятся в следующих местах.
Поскольку диаграмма равноудалена, изобары перемещаются влево по мере увеличения давления, а вправо — по мере увеличения объема изолиний increases. By применяя исследуемый процесс к полю, становится возможным графоанализ Быстро определяют параметры рабочего тела в любой точке технологического процесса и рассчитывают изменения внутренней энергии, энтальпии, работы, теплообмена с окружающей средой и др. Термодинамические природные процессы всегда направлены на достижение системой равновесных состояний(механических, тепловых или иных).
Это явление отражено во 2-м Законы термодинамики имеют большое значение для анализа поведения тепловых генераторов. Согласно этому закону, например, тепло может передаваться только спонтанно От высокотемпературного тела к низкой температуре village. To унесите обратный процесс, некоторая работа required. In в связи с этим Второй закон термодинамики Его можно сформулировать следующим образом: процесс естественной передачи тепла от холодного к теплому человеку невозможен(предположение Клаузиуса).
Второй. Кроме того, законы термодинамики определяют условия, при которых тепло преобразуется в работу до тех пор, пока это необходимо. Открытый термодинамический процесс с увеличением объема Положительная работа осуществляется[по ссылочным формулам (1.37), (1.38) J, однако, поскольку процесс расширения не может продолжаться бесконечно, возможность преобразования тепла в работу Ограниченный. Непрерывное преобразование тепла в работу осуществляется только в процессе циркуляции или цикле (см. Рисунок 1.4).
Все основные процессы в цикле Подача тепла DQ (ds> 0) или запуск при отводе тепла (ds <0), сопровождающийся завершением работ dL (dv> 0) или стоимостью (dv <0), увеличением (dT> 0) или уменьшением если внутренняя энергия (в случае dT <0), но всегда выполняется условие (1.39).Интеграл условия (1.39) на замкнутом контуре равен$ dQ-Q {ᵢ,$(IL = — Ц, потому что / du = 0. — Соответственно, тепло в цикле преобразуется в работу, выполняемую работой и рабочим телом, то есть разница (Li | — / L₂1 положительная и отрицательная работа Основной цикл процесса.
Рисунок 1.4 работа Li характеризуется областью ниже процесса 1D2, где Lj-область ниже процесса 2C1.Следовательно, L определяется занимаемой площадью Цикл. Основным количеством теплоты можно считать подачу (dQ> 0) и отвод (dQ <0) от рабочего тела. Сумма общей теплоты в цикле / Qi|, а также выделенное количество Тепло I 0,2 I-соответственно(1.П9.)^ = ^ = 1(211-1(22 если внешний источник с температурой над I-температурой, то он может поставить количество Q heat жары к рабочей жидкости.
Рабочая жидкость. Такой источник тепла в дальнейшем называется высокой температурой. Удаление количества тепла Q2 из рабочего тела возможно даже при наличии внешнего источника тепла, но при этом температура Ниже, чем температура рабочей жидкости. Такой источник тепла ниже называется прохладным воздухом (см. Рисунок 1.4).Поэтому, чтобы завершить цикл 1D2C1, вам нужно 2 источника. Жара: 1-ая высокая температура и 1 Т₂ low. In кроме того, количество тепла Q2 передается, поэтому не все количество тепла Qi потребляется будет работать. Холодный соус.
Условия эксплуатации теплового двигателя следующие: 2 источника тепла (высокая температура и низкая температура) нужны. Периодическая работа двигателя. Движущиеся части Количество тепла, полученного от горячих источников, холодное без превращения его в work. In в связи со 2-м законом этой термодинамики можно сделать еще несколько формулировок. Тепло от низкотемпературного источника до высокой температуры невозможно без работы costs. It невозможно построить регулярно работающую машину, выполняющую механическую работу, и поэтому.
Охлаждение теплового резервуара (предположение Томпсона); природа стремится перейти из маловероятного состояния в Высоковероятное (Больцман).Тепловая эффективность. Результаты работы Согласно формуле цикла (1.119), он определяется разницей в работе расширения А и сжатия/₂/, следовательно, он становится/ > /и/,,, > 0.Чем выше КПД двигателя, тем больше работа. Рисунок 1.13 получен при заданном слэте тепла. тепловая эффективность цикла Карно vp и «T > координаты П» = b) однако существуют обратные циклы, которые совершаются за счет внешней работы.
Крючок, рисунок цикл 1.4 соответствует обратному циклу 1C2D1, направленность Процесс обозначается пунктирной линией со стрелкой. Обратный цикл из-за стоимости внешней работы| g₂I-14i I = — / c тепло перемещается от источника холода к источнику тепла source. By Охладитель работает в таком обратном цикле. Коэффициенты охлаждения e,= t/₂, для оценки эффективности их работы//«= 42 /(42-41)-(1.122)он используется, когда Идеальный процесс циркуляции необходим для анализа работы теплового генератора. Французский физик С.
Карно предложил цикл Карно в 1824 году、 Термодинамический процесс (рис. 1.13), обеспечивающий наиболее полное преобразование тепла в работу. 2 Процесс AB и CD происходит при постоянной температуре(изотермический) Соответственно, Il = const и T₂= const, а T >T₂.Процесс BC и Da адиабатические и работать без теплообмена с внешней средой, например, йд = 0. (1.46) первый закон термодинамики(]ₐₕ- & UAB + Lab’, 0 = Dis + IBC’, (Jed = auₜd + l ₍d; 0 = AW * 4-LDₐ.Внутренняя энергия не изменяется при постоянной температуре (Di * = 0; DmG4 = Поскольку изменение внутренней энергии адиабатических процессов bt и da, происходящих при 0X и в одном температурном диапазоне, одинаково (Am ^ a = Li*), на работу цикла/ c+ Ibc I hd I это не влияет. I Ida I Vantage VaI Qcd I и тепловой КПД Пг ^ 1〜14ы1/ 14 < * 1.
Согласно рисунку (1-123), 4y = b(Ъ< — a) и<<—Tₜ(sb-sₐ).Тепловая эффективность-полезно для отношения Общее количество тепла, потребляемого в цикле q2 от теплоты di, используемой в цикле (или приобретенной работы / Bragg/).Цикл Карно является обратимым циркуляторным процессом. Наиболее полное превращение (или превращение из работы в тепло) из тепла в работу. sₑ-sd = sb-sₐ, поэтому<= = I-T ^ / A (1.124) определяет эффективность цикла Карно. Соотношение температуры источника тепла при высоких и низких температурах. Его значение увеличивается с увеличением D или уменьшением на 7g. если нет разницы температур в источнике тепла (Т₂= Ti) тепловой КПД n, = 0.
Цикл Карно состоит из обратимых процессов, поэтому он обратим (пунктирные стрелки).Особенности обратного цикла Карно Со стороны на работе| c |2 / —1 < / 1!=- /«; С другой стороны, тепло от холодного источника тепла передается к источнику тепла. Это коэффициент чиллера, основанный на цикле чиллера, формула (1.122)^ = 1 /(Т,/Т₂-)=Т₂/(Т₁-Т₂}(1.125)цикл Карно является особый температурный режим максимальной тепловой КПД т | ф с 7]-Т₂. Диапазон температур и энтропии (пунктирная линия) приводит к уменьшению площади цикла, что в свою очередь приводит к уменьшению теплового qₙ, которое преобразуется в функцию в цикле и становится меньшим значением.
Тепловая efficiency. As как показано в уравнениях (1.124) и (1.125), тепловая эффективность и коэффициент охлаждения цикла Карно не зависят от физических свойств рабочего тела (теорема Карно). Он не содержит количества, характеризующего характеристики рабочего тела. Термодинамическая шкала температуры. Температуру нельзя измерить сразу; свое значение Температурные изменения физических свойств веществ удобно измерять, например, тепловыми свойствами теплового расширения (ртуть, спирт и др.).
Линейная зависимость изменения объема этих веществ от температуры зависит от Удельной(и Различные свойства вещества используются в термометрах. Тепловой режим и шкала температуры кэша не зависят от характеристик рабочего тела. Из сравнения формул (1.121)и (1.124) Поэтому\q₂l / Uil = Wi и Ifli l / l <121 = /(n; t₂).Где ti и t₂-температуры, полученные на эмпирической шкале температур. Тепло qᵤ = / < / 1 | -| q₂ / преобразуется в рабочем цикле и не зависит от способа измерения этих температур. В течение 3 циклов Карно (рис. 1.13), эбед, demn, и abnin поддерживаются. L » il / l ^ 2l = /(ti; t₂\ l < / ₂ / l ^ l = /(t2; h) И I <7i l / l dz / = / (fi; * з) — если умножить первые 2.
Формулы после семестра и сравнить произведение с 3-м равенством, то получится следующее: Ф (tₓ;t₂)Ф (t₂;t₃)= /(ги ч) — потому что t₂ не вступает в права,/ 0i; = Φ () / Φ (H) и<(t₂;следовательно, 1 / 1, функция φ0) положительна и возрастает с увеличением температуры. Температура источника тепла от низкой до высокой температуры、 Согласно формуле (1.126), Ф0)=о0)/ ’0;go). Для представления положительного значения Ф0), то ф0)=термодинамическая шкала температуры основана на 2-м начале Термодинамика определяется и будет определяться с использованием никеля Карно. Рисунок 1.14. ИС Диа! cycle frame = to) .
Если выбрано значение Then и значение не зависит от метода измерения Для выбора значения температуры 7°, например, поскольку функция φ ® не зависит от термометра, температуры и типа используемого термометра、 Температура плавления льда и кипящей воды равна t₀ и tb, если измерять каким-либо образом, то соответствующие термодинамические температуры равны To и Tb. φ ( ₀₀ ) = 7 ^ Φ (0>)=Tₕ= Tof(tb \ to).В зависимости от диапазона температур, разделите диапазон температур от до 7 ^ NS равным. Число делений будет равно числу делений по шкале .
Цельсия. е.100.Тогда to / ’(rb; R) — To = 100°C, whice to = 100 / [f(tb; to) −11, или рассмотрим(1.126)7o = 100 / [/s / 1oo 1/1 I-1], (1.127) где 9yu s 91-калорийность、 Температура Tx =t₁₀₀ (температура кипения крупного рогатого скота при атмосферном давлении) 1 кг рабочего тела, полученного в обратимом цикле Карно из пружин. | < / ₀1= = I 921-абсолютный Количество тепла, которое отдается источнику холода при температуре 1 кг рабочего тела при температуре 7°с, тает в том же цикле. Экспериментально установлено, что I 9yo 1 / 19o I = 1,366. Отсюда до = 273.15 К.
Когда температура падает до, эффективность цикла Карно [опорное уравнение (1.124)] возрастает, и d)= 1 (T2 = T0 = 0 K(t = −273.15 * C)).Дальнейшее сокращение Температура, дайте T|, > 1.Это противоречит второму закону термодинамики. Таким образом, температура T = 0 K или t = −273.15 ° c равна、 Точка отсчета для шкалы абсолютной температуры. Изменение энтропии процесса с потерями. Из соединения (1.121) и(1.124), в случае обратимого цикла Карно 191Г— / 92 (/7’ä = 0.(1.128) в этом соотношении, если мы явно рассмотрим 91> 0 (тепло подается в рабочую жидкость) и 92 <0 (тепло удаляется из рабочей жидкости), уравнение (1.128).
Принимает вид 9i / Ti + = 0.- (1.129) полученное соотношение является основным циклом Карно ahhem, полученным при любом обратимом пересечении (рис. 1.14) Адиабат бесконечно отдаляется друг от друга. Так как точки a и b, c и t бесконечно близки друг к другу, то температура рабочего тела T°= T в Точки cl и / >и 7 =Т₂ точки C и M. в этих условиях процесс AH и CT являются изотермами, а цикл ahem является базовым циклом Карно, где < / 91/71 + D (ᵢ1 / /T = 0.(1.130) Обратимый цикл может состоять из нескольких основных циклов Карно. Непрерывный набор основных Изотерм в этих циклах образует любой обратимый контур Цикл.
Для каждого базового цикла Карно можно получить отношение (1.130).Если вы интегрируете все отношения обратимого цикла, вы получите jdqₗ / Tₗ+fdq₂/T₂= 0 (dq}> 0,dq₂<0). Передайте изоляцию! Это вперед и назад, так что это не влияет на состояние работы fluid. In в связи с этим консолидация осуществляется только по произвольному контуру Цикл, и если этот цикл состоит из обратимых процессов, то учитывают$ dq / T = 0 (1.131) или формулу (1.49) ps = 0.(1.132) поэтому、 В результате любого обратимого цикла энтропия рабочего тела не изменяется.
Необратимый процесс, цикл работ, выполняемых при прочих равных условиях, необратим Не-обратимый процесс, и qfh не <П»о-следовательно, если есть необратимый процесс в цикле dqJT \ +dq₂/T₂<0 или$Л/Т<0 после интегрирования по контуру. (1.133)например, в любом цикле Рис. 1 1.14 процесс ak₂ необратим, а kiccia обратим. Интеграл (1.133) может быть выражен в виде суммы\ dq / T + f dq / T < V. ₜ > dq / T, (1.134) масло здесь < / sh-фундаментальное изменение энтропии необратимых процессов. Если процесс ak}обратим, то изменение энтропии отражается в процессе kicc(a (точка k \и a Генерал.)Таким образом, энтропия возрастает за счет необратимости процесса nlij.
Когда-то вывод об увеличении энтропии в изолированных системах был: R. It именно тогда Клаузиус пришел к следующему выводу. Неизбежность»тепловой смерти» Вселенной. Это должно происходить тогда, когда бифуркация всей энергии Вселенной переходит в энергию теплового движения, которая равномерно распределена по всему телу. Сущность вселенной. Тогда все макроскопические процессы прекращаются. Р. Это утверждение Клаузиуса убедительно опровергается современным космологом! Ее.
Учитывая гравитацию Как интегральное свойство Вселенной, мы можем видеть, что изотермическое распределение энергии во Вселенной не является наиболее вероятным. Вселенная быстро нестабильна Материал расширяется, и в начале расширения под действием гравитационных сил самые однородные вещества разлагаются со временем, образуя галактики, звезды и планеты. Эти процессы полностью Соответствуют законам термодинамики (в результате энтропия возрастает), они всегда выполняются, поскольку являются свойствами Вселенной.
Следовательно, максимальная энтропия То, что ищет Вселенная, недостижимо, и»Тепловая смерть»Вселенной-это impossible. In цикл необратимых процессов, энтропия изолированной системы возрастает. Эксергия 7 Exerpo определяется в виде dq = di-vdp по формуле (1.52). (1.135) произведение g-координаты ВДП(см. Рисунок 1.11) Основная панель на левой стороне процесса. Поэтому есть единица работы. Основная работа dLo = — V dp или L₀= — & dp(1.136) В отличие от расширенной работы (1.38), одноразовые. Если рассматривать (1.136), то уравнение (1.135) можно представить в виде dq-di + dlo.(1.137) или .
В рамках конкретного термодинамического процесса 12 (столбчатая диаграмма, 1.8, d) 2 sdq〜i₂-iₗ+2₀, (1.138) 1 I2 /о определяется площадью Г122′. Если процесс является обратимым 12, тогда 2 Джей и DQ / Т = С2-СИ-1, Если процесс 12 необратима, тогда в соответствии с неравенством (1.134), 2 Джей и DQ / Т <С2-Си. 1 указывает на увеличение энтропии из-за золы Из-за необратимости процесса, 2 f dq / T + Si-si + As,, =0.(1.139) умножает все члены Формулы i (1.139). Внешняя среда 2.1 (to / T)dq +(si-Sj) To + L3 ″ из 7o =О1 вычитаем полученное таким образом уравнение из левой части уравнения (1.138): 2 f (Т-To)dq / T = i₂-h-7o (- s2-Si)+ i 2 +TₒAs,, +l₀. 1 (1.140) как указано, процесс в системе является обратимым (A $и<= 0), и работа максимизируется до тех пор, пока состояние продолжается Равновесие с внешней средой с параметрами ПО и К.
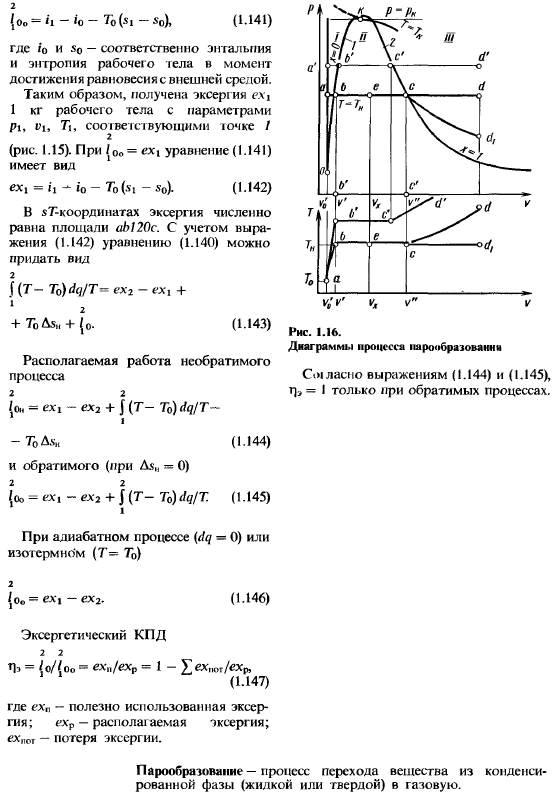
Такой процесс может быть представлен непрерывным набором из 2 обратимых процессов. Изоляция/ 2 Ti до Т₂ = то и изотермической 20 (рис. 1.15), т=7О= const для течения при P =P₀.Выбор этого процесса приводит к тому, что левая часть выражения (1.140) равна нулю(dq = 0 И Т = К).Максимальная работа, выполняемая рабочей жидкостью в случае холодной эксергии или технического исполнения Источником тепла считается внешняя среда, в которой находится температура. 2 {о₀= * 1 «* 0-7₀ (- Ч-⁵о), (1-141), где r’о и о являются энтальпии к энтропии тока рабочей жидкости, соответственно.
Достичь равновесия с окружающей средой. Таким образом, мы получили параметры Pi, которые соответствуют точке/ 2, рабочей жидкости 1> 7i> 1 кг Эксергии(рис.1.15).Когда| ОО =Форма уравнения (1.141)= h * a0-To (x» — 5₀) — (1.142) в координате sT Эксергия численно равна квадрату a20.Учитывая формулу (1.142), можно дать формулу (1.140) Форма 2 f (T-T) dq / T»=ex₂-exi + * +ToAs,,, + {₀- (1.143) 2 {uand = ex + J (T-to) DQ / T- -T₀Ash(1.144) и обратимый (As, = 0)2 2 {ω= eXi-ex₂+ J(T-T ^ dq / T.(1.145) 1 рисунок 1.16.
Схема процесса выпаривания Выражения (1.144) и (1.145),=только обратимый процесс. Процесс изоляции (dq-0)или изотермический (T = To) 2 / Oo = ex> — ex₂. (1.146) Exgrstich эффективность 2 2 Pe = (o / {oo » exp exp = 1 — £exp₁₁r / exp, (1-1raid) где EXP-полезная используемая Эксергия, где EXP осуществляется, Schroth-потеря. Это отличное приложение. Испарение-это процесс, при котором вещество переходит из конденсированной фазы (жидкой или твердой) в газ.
Смотрите также:
| Теплообменники регенеративного типа | Термодинамические процессы реальных газов и паров |
| Основные понятия и определения | Истечение, дросселирование газов и паров |

