Оглавление:







Основные уравнения теории вихрей и теоремы Гельмгольца о сохранении вихрей. Введение
В главе потенциал скорости. Вектор скорости представлен как наклон этой функции, поскольку в идеальной жидкости существует множество таких движений. Эти движения гидромеханики идеальной жидкости являются движениями с потенциальным потенциалом скорости или движениями без вихрей жидкости. Последнее название объясняется тем, что вихрь скорости исчезает против движения с потенциалом.
Дело в том, что вихрь скорости является вектором, составляющая которого определяется по формуле. Условие выполнено, то исчезает. Например, компонент вихря скорости вдоль оси выглядит следующим образом. Следовательно, если вычеты комплексной скорости, циркуляция и поток скорости. В общем случае для функции всегда. Заметим, что напротив, условие означает уравнение. Как указано в расчете вектора. Поэтому, вращательные движения, вероятно, существует скоростных возможностей.
Целью данной главы является рассмотрение движения идеальной жидкости, вектор которой — вихрь вектора скорости — не равен нулю по крайней мере в части рассматриваемой жидкости. Этот вид движения называется вихревым движением жидкости. Движение вихревой жидкости можно обнаружить во время самого основного наблюдения. Это, например, движение речной воды в местах, которые протекают вокруг моста Быков.
За последними находятся области вихрей, которые хорошо видны. Когда тело движется в жидкости, такой как корабль, позади него также образуется вихрь. Необходимо потратить теорему Томсона некоторую энергию на формирование этих. Понятно, что эта энергия получается за счет энергии тела, и поэтому необходимо преодолеть сопротивление жидкости. Это сопротивление, вызванное образованием вихрей, называется вихревым сопротивлением.
Циклоны и антициклоны, рассматриваемые с гидродинамической точки зрения, в некоторой степени определяют погодные условия в тех местах Земли, где они расположены, а также представляют собой образование вихрей. Торнадо — еще более острая форма вихревого образования в атмосфере. Кинематика вихревого движения была частично изучена в Главе. Вспомните некоторые определения и следствия из этой главы.
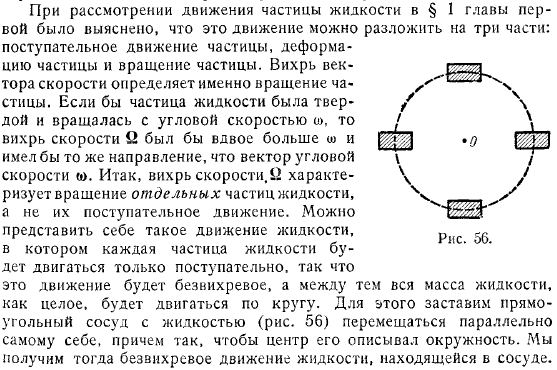
Если мы рассмотрим движение частиц жидкости в разделе Главы, то увидим, что это движение можно разбить на части: поступательное движение частиц, деформация частиц и вращение частиц. Вихрь вектора скорости точно определяет вращение частиц. Если частица жидкости является твердым телом и вращается с угловой скоростью, то вихрь скорости равен раз и находится в том же направлении, что и вектор угловой скорости. Это вихрь скорости и характеризует вращение отдельных частиц жидкости, а не поступательное движение.
Теорема разложения Гельмгольца — утверждение о разложении произвольного дифференцируемого векторного поля на две компоненты. Людмила Фирмаль
Вы можете представить себе движение жидкости, когда каждая частица жидкости движется только вперед. Это движение обусловлено отсутствием вихрей, во время которых вся масса жидкости движется круговым движением в виде. To для этого прямоугольную емкость с жидкостью перемещают параллельно себе, так что ее центр представляет собой круг. Далее вы получите не вращательные движения жидкости в контейнере.
Примером обратное движение жидкости из слоя, определяется по формуле. Каждый слой жидкости, параллельный плоскости, движется параллельно оси, увеличивая скорость движения. Чем дальше рассматриваемый слой находится от плоскости. Итак, в этой операции рассматриваемая жидкость скручивается. Дело в том, что квадрат, состоящий из жидких частиц деформируется при движении и становится параллелограммом за этой деформацией следует преобразованный квадрат в направлении стрелки, как показано в Главе, вдоль чистой деформации (в данном случае натяжение вдоль линии a и сжатие вдоль линии).
Поэтому необходимо обратить внимание на различие между обыденным понятием вихревого движения как движения типа круга и гидродинамическим понятием вихря, описанным только в Главе выше. Возможно, разница в этом термине должна быть затенена, но в соответствии с общепринятым термином. Вспомним определение вихревых линий: вихревая линия такова, что вихрь скорости направлен тангенциально к этой.
Форма уравнения вихревых линий. Возьмем замкнутую линию и проведем вихревую линию через каждую ее точку, тогда совокупность всех таких вихревых линий ограничит вихрь. Глава, была очень тесная связь между понятием вихря вектора и понятием циркуляции вектора вдоль замкнутого контура, и было выбрано конкретное направление.
То есть, принимая мизерный плоский контур, циркуляция скорости вдоль этого контура равна произведению площади, покрытой контуром, и составляющей вихря скорости, взятой в направлении, перпендикулярном плоскости контура. В этом случае вы используете правильную систему координат, поэтому направление контура должно быть ориентировано в направлении пространства, которое, по-видимому, относится к часам.
Проекция собственного направления вектора имеет наибольшую величину по сравнению с проекцией вектора в другом направлении, поэтому если плоскость контура вращается по-разному, то циркуляция будет максимальной, если этот контур перпендикулярен плоскости направление вихря равно формула может быть обобщена для контура конечного размера, где задано конкретное направление обхода. В этом случае это называется выражением Стокса и имеет следующий вид: является элементом этой поверхности.
Проекция вектора вихря в направлении перпендикуляра к поверхности элемента, выбранного в соответствии с. Кроме того, было отмечено, что расходимость вихря всегда равна нулю, и с помощью этого была доказана следующая теорема о постоянстве циркуляции по вихревой трубе: величины циркуляции по замкнутому контуру, окружающему эту вихревую трубу, равны друг другу.
Это значение циркуляции было названо силой вихревой трубы. Для микро-вихревой трубы ее прочность равна произведению микро-сечения вихря и трубы, перпендикулярной его оси по формуле. Теорема о постоянстве силы вихревых труб вдоль оси была установлена Гельмгольцем, создателем теории вихрей.
Если дивергенция и ротор векторного поля пределены в каждой точке конечной открытой области пространства, то всюду в функция может быть представлена в виде суммы безвихревого поля и соленоидального поля. Людмила Фирмаль

