Оглавление:




Асимптотические решения задач дробно-линейного программирования
- Асимптотическое решение задачи Дробное линейное программирование Для неограниченного региона L возможных решений Одна или обе ее крайние задачи Асимптотическое. С геометрической точки зрения в этом случае Разрешение вращающейся гиперплоскости вокруг начала координат.
- Приближение к позиции, параллельной бесконечному ребру (Рисунок 15; 16). Необходим для решения линейных дробных задач Программирование и настройка модифицированных симплекс-методов Символ анализа существования асимптотических решений. Как и прежде, рассмотрим стандартные вопросы (2) — (4). Неоптимальный на шаге симплекс-метода Решение этой проблемы.
Иначе, вектор определения puv (Ak) вводится в базу по формуле max (Δ,) = Δ *> 0. Людмила Фирмаль
Вы не можете выбирать элементы разрешений в столбце разрешений. Это все Xik <0. В этой ситуации обычная проблема Возможности линейного программирования безграничны. Однако при линейном дробном программировании целевая функция Соотношение двух линейных форм. В этом случае Неопределенность в виде ~ раскрывается.
Раскройте такую неопределенность Один из известных методов (например, расчет лимита) (Прямо или в соответствии с правилами Lopatel), вы можете получить Конечное число и бесконечность. 122 Конечно, в изучаемой ситуации Переменная Xk вводится в базовом решении. Эта переменная Это происходит от того, как построить базовое решение.
Увеличение произвольно с новыми работоспособными решениями Значение. Покамест Симплекс стол xrk. Тогда в результате одного шага полного метода Исключением для (s + 1) -й таблицы является новый действительный Решения с одинаковыми значениями функции (см. 11): «Χι zts + 1) = z (‘s) -f; (Zi * -c’ *> = z \ «-Xk (от zlk до clk) (i6) В уравнении (16) единственной переменной является x *.
Напомним, что ΔΛ> 0, разность Z \ k-с \ н и Z2 * -c2k Он не может быть нулем одновременно. Так возможно Два случая: / Дело. Разница Z2k-c2k = 0, тогда ΔΛ = Z ^ (Zik-сХк). Предполагая ΔΛ> 0 и s ^> 0, Z (s + 1, = Φ-Mflk-l * и HmZ (s + l) = _о0в Последнее соотношение означает неограниченное Функция линейной дроби: В этом случае процесс расчета Выход. 2 случая. Z2k-c% k = f = 0 тогда HmZ -. xk (Ζ, k-ctk) \ d * k {4s, — ^ (22ft-c2fc)} 2 = — ^ (Zik ^ clk) + Z ^ (Z2k-c2k) = -A «
Из уравнения (18) и предположения, что ΔΛ положительно: дЗ (с + л) Производная ———— <0, то есть функция монотонна 1 фут «™ ^ фут * -ч Уменьшение и приближение к конечному пределу — = -. Это L2k ^ c2k Номер. Асимптотический минимум целевой функции Задача. Очевидно, что в пространстве размерности n> 2 число ребер Бесконечный многогранник L есть По сравнению с двумерным случаем он значительно больше.
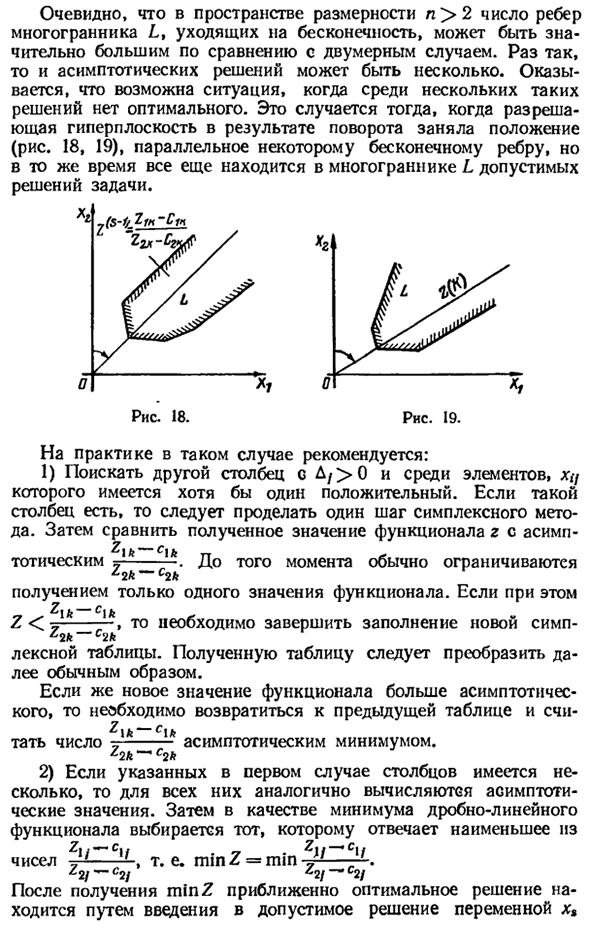
Если так После этого может быть несколько асимптотических решений. Вы можете видеть, что ситуация возможна в некоторых таких случаях Там нет оптимального решения. Это Решение гиперплоскости в результате вращения занимаемой позиции (Рисунки 18 и 19) Параллельно бесконечному ребру, В то же время он остается разрешенным многогранником L Решение проблемы.
Рисунок 18. Рисунок 19. На практике в этом случае рекомендуется следующее: 1) Ищите другой столбец g D /> 0 и xif в элементе Есть как минимум один позитив. В таких случаях Если есть столбцы, вам нужно выполнить один симплексный шаг Метод. Далее сравниваем полученное значение функции r с асимптой тототический =. До тех пор, как правило, это ограничено Получить только одно значение функции.
- В то же время Г-s Ζ <・ =, тогда вам нужно завершить ввод нового символа Z2fe ~~ C2fe Рекс стол. Полученную таблицу необходимо преобразовать Обычным способом. Если новое значение функции велико Если асимптотика, вам нужно вернуться к предыдущей таблице, Количество их Z2k * -c2ft Асимптотический минимум. 2) Если столбец указан в первом случае.
Некоторые из них рассчитываются одинаково Асимптотическое значение. Тогда как наименьшая линейная дробь Функция выбирает самый маленький числа 5lT5L, т. Е. ммЗ = мин5у ^ — Z2j-c2 / Z2! -c2 / Практически оптимальное решение после получения minZ.
Найдено путем введения переменной x * в допустимое решение (Смотрите, как построить базовое решение). Людмила Фирмаль
Добавить к переменной большое положительное значение для хз, вы можете получить решение, Почти оптимально для любого. Также соответствующий Значение функции не будет сильно отличаться от предела Zlfe-c \ k Следующие рекомендации обосновываются следующей теоремой. Теорема 4. В случае асимптотических значений найдено.
Вы можете указать функцию линейной дроби указать Решите проблему, где меньшее значение меньше, чем многогранник L Некоторые экстремальные значения имеют меньшие значения Данный лимит. Доказательство. Нарисуй это наоборот. Сделать гиперплоскость, чтобы решить параллельно Бесконечные ребра и функции из области L Предельное значение Ζ (&) «.
В этой позиции гиперплоскость разбивает выпуклое множество Разделите L на две части. Одна из этих частей, Указанное эффективное решение с функциональными значениями лжи Не существует экстремальной точки для Z 4; 2xx + x2> 6; с ограничениями -x2 + x2 <3; χχ> 0, x2> 0. (20) Приведите проблему ограничения к стандартному формату. -A «! + 3×2- * 3 = 4; 2 *, + x2-. X4 = 6; ~ xx + x2 + x5 = 3; x9> 0, / «1, …, 5. (21)
Вместо этого, чтобы уменьшить количество искусственных переменных, введенных Второе и первое из первой формулы (21) Те же системные ограничения. Тогда, во втором ограничении, искусственный В результате переменная * in получает следующую условную систему. 3 *! -4χ2 + * 3- ^ * 4 = 2 «» 2 * 1 + * 2— * 4 + * 6 = βΙ ” — * 1 + * 2 + * 5 = 3 xj> G> / = 1, …, 6.
Заполните и преобразуйте первую симплексную таблицу * (Таблица 4) Чтобы получить базовое решение исходной задачи. Приемлемое базовое решение проблемы содержится в габ. 6, л ^ д 308 Вычислить определитель Δ. Поскольку Δ4 = -j-, положительное единство Количество слагаемых Δ. Если все коэффициенты в четвертом столбце не являются положительными, *
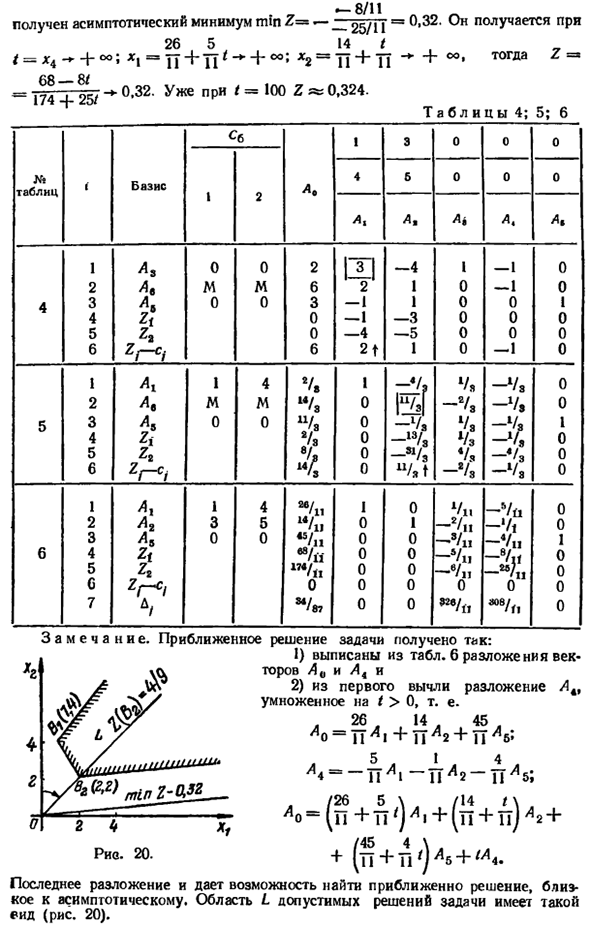
Искусственный столбец At опущен. 125 -8/11 Асимптотический минимум Z = -_ 25 / 11β0,32 < 26 5 14 * / = χ4 ^ + оо; χ1 = γγ + χϊ ^^ + оо; ^ 2 == ΤΤ + Ή «* + оо ・ Т0ГДа СО ^^ Ο / • 0,32. Уже * = 100Ζ «0,324. Замечания. Примерное решение задачи получается следующим образом: 1) Разряжается со стола.
6 расширений Векторы A0 и L4 и 2) Разборка AA9 была вычтена из первоначальной разборки Умножим на t> 0, т.е. 26 л 14 и 45 я Ao = T \ A1 + PA2 + PA 5 1 4 / 26 5 \ / 14 т \ Αο = (η + Τι <) Αι + [Τι + η) Α2 + (R \ + T \ ‘) Av + <A4 + При окончательном разложении приближенное решение может быть найдено. Рядом асимптотика. Возможная область решения проблемы L Ид (рис. 20).
Смотрите также:
Примеры решения задач по математическому программированию

