Оглавление:

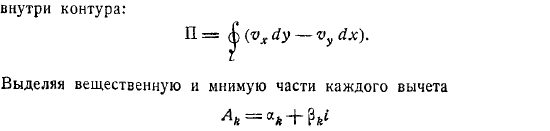
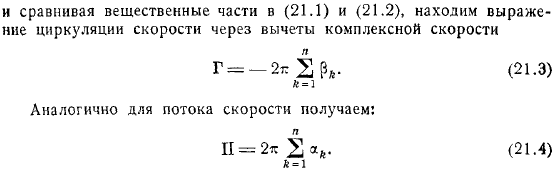

Вычеты комплексной скорости, циркуляция и поток скорости
Как известно из теории функций комплексных переменных, структура аналитической функции гидромеханики полностью определяется распределением в плоскости особенностей функции и ее свойств. Если распределение комплексной скорости простого полюса и соответствующие остатки известны, теория остатков может легко выразить циркуляцию и поток скорости вдоль любого. Дело в том, что простым полюсом функции является точка и соответствующий остаток находится в. Если это, то для замкнутой цепи, содержащей линейный интегратор функции вихреисточников , получим.
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания, умножения и деления. Людмила Фирмаль
С другой стороны, разделение действительной и мнимой частей происходит следующим образом. В действительной частью является скорость циркуляции по контуру. Объем жидкости, вытекающей из источника в контуре. Выберите основные уравнения теории вихрей и теоремы Гельмгольца о сохранении вихрей действительную и мнимую части каждого остатка и сравните действительные части, чтобы найти уравнение циркуляции через комплексную скорость оценки скорости для скорости потока, а также.
Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше. Людмила Фирмаль

