Оглавление:




Двойственный симплексный метод
- Двойной симплекс-метод Из предыдущего абзаца в этой главе, матрица Факторы для основных ограничений двойной проблемы Транспонирован по системной матрице Условие исходной задачи. Обратное также верно. Кроме того, из основной теоремы двойственности: Знает лучшее решение для одной из пар двойных задач, Вы можете получить решение для оставшихся проблем.
- Предположим, что исходная задача написана в нормальной форме Форма. Минимизировать выравнивание L z = I] q * / O) В условиях n (2) ΣaifXf = aiy i = 1, 2, …, m \ * x > 0, u> 0, / = 1, 2, …, n; i = 1, 2, …, m (3) Получим симплексную таблицу задачи (1) — (3). Включает некоторые неоптимальные базовые решения. тогда Вводимый в базу вектор Ak определяется максимальным значением.
Положительная разница max (Ζ, -q) = Ζκ-ck> 0 и вектор (Ls), получаемый из базисно-минимального симплекса. Людмила Фирмаль
Отношения: , hhχι мм— = ・ = -. xik xrk Для лучшего решения все различия Z / —C / <0. Двойной симплекс метод используется для решения У меня есть проблема линейного программирования Стандартная форма каждого уравнения является основной переменной Перед решением проблемы коэффициента +1 или -1 Двойной симплекс-метод, стандартная модель задачи Умножьте каждое уравнение для преобразования.
Переменные с коэффициентами от -1 до -1 после такого преобразования 86 Существует основа для каждого выражения ограничения Переменная с коэффициентом +1. Но мне пришлось отказаться Из неотрицательного состояния соответствующей части, то есть после В правой части основных ограничений, как правило, Есть отрицательные числа.
Для ограниченных систем Учитывая задачу выписывания базового решения, Неприемлемо, то есть не удовлетворяет неотрицательным условиям Переменный. Именно из этого неприемлемого решения исходной проблемы Решение этой проблемы начинается. Такое недопустимо Исходное решение проблемы встречается с неверным решением.
Двойная задача В двойном симплексном методе цепочка строится Оригинальное решение проблемы и соответствующий набор решений Двойная задача: Xlt X2 ,,. , , X /, X * -j-l, Α * _ | 2ι ・ ・ ・ »lr, X0rm Yl Y2, … Yu Yu, Yt + 2, … YD, * оптом Цепочка начинается с перехода на лучшее решение Yb y29 …, поднят на неверное решение.
Двойное задание не принимается в общем случае Решение X | e X1, …, X / исходной задачи. Первый этап Расчет заканчивается поиском возможного решения Yg Двойная задача, это все еще распространенный случай Соответствует неверному решению Χ * + ι исходной задачи. Такой первый этап расчета для целей приобретения.
Неверное базовое решение Y до приемлемого базового решения Решение Yg создается следующим образом: 1) Сначала произвольно выбирается первая строка Симплексная таблица I (вектор A /, полученная из базы), и 2) Вектор, который вводит L * в основание (первый столбец) Simplex table), по крайней мере, в двойном Симплекс отношения.
Двойной симплекс Первый этап расчета положительный или Равно соответствующему ненулевому но точно Положительный элемент ведущей линии. Вот так Минимум J ^ = iZii> 0 (/ = ср). / Ζ} -η> 0 \ * ri Lgk ° ‘> ° J Первый этап расчетов легко угадать Двойной симплекс-метод, направленный на уменьшение количества Положительная разница и уйти вообще Разница Ζ / -ίγ <0.
- Тем не менее, все в порядке (значение Базовая переменная c. Xr-μ) неотрицательный, Χ / + ι — лучшее решение исходной проблемы, а Yg — лучшее решение. Двойная задача Проблема была решена. В общем случае Правая часть (значение базисной переменной Xf + i) Значение является отрицательным числом. В этом случае перейдите к (Второй шаг в расчете.
Целью второго этапа является поддержание эффективности. Двойное планирование проблемы (не положительно для разницы Z, — -Cj), добейся всего не отрицательного Ограничение (значение соответствующей базисной переменной Основное решение исходной проблемы).
Конец этих решений Aopt и Dual-ownedοητ * принадлежат выше. Людмила Фирмаль
Свойство и лучшее решение желаемое. движение Согласно оптимальному плану 双 0Ώτ двойственной задачи * Приемлемое решение y / + 2t ..-, двойная задача ур, Горячие и копт неприемлемые решения исходной проблемы устранены. Последние решения Hot и solutionsτ — лучшие Рассмотренное парное решение для двойных задач.
Если делать Обратите внимание на последнюю симплекс таблицу, содержащую Оптимальные решения Hopt и FGrm все разности Zf-C / <0 и все Правая сторона (значение базисной переменной) Ограничение не отрицательное. Целью второго этапа расчета является Следующие правила: 1) Первый Le чтение строки r выделено (вектор Ai-ASrt (Получено из основания симплексного стола).
Отрицательное право (отрицательное базовое значение Неверная переменная решения для исходной задачи) Ограничение, то есть mmβ <= i / <0; (° t <°) 2) Вектор Ak введен в основании (первый столбец k Симплекс стол), маленький двойной Симплексные отношения для второго этапа расчета.
Вторая стадия двойных симплексных отношений — это отношения Абсолютная отрицательная или нулевая разница с соответствующей Тем не менее, строго отрицательный элемент в первой строке, т.е. Минимум ZJf ^ L = Z ^ pft> o (/ = 5Λ). (Zf-cf <0 \ lχπ <«) xrj * rk Такой выбор предшественников четко сохранился Неположительная разница Z / -Cf и числа не увеличивается Отрицательный правый предел.
На втором этапе В расчете между элементами Там нет отрицательных линий. Первоначальная проблема противоречива. Поскольку соответствующий предел не соблюден: χι = * = Σ * r / * / t где Ν — множество неосновных значений Пояс. Здесь xt <0 слева, — Все неосновные переменные * /> 0 и x > 0 Все / € N Поэтому на втором этапе устанавливается несостоятельность.
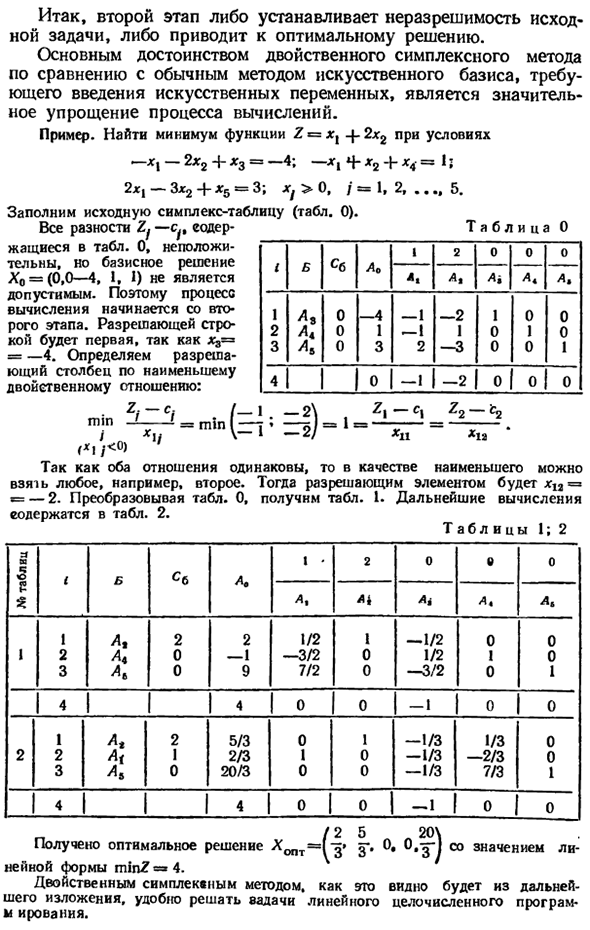
Это приводит к исходной проблеме или лучшему решению. Ключевые преимущества двойного симплекс-метода По сравнению с обычным методом искусственной основы, Необходимо ввести искусственные переменные Значительное упрощение процесса расчета. Пример. Найти минимум функции Ζ = xy + 2jc2 при условиях , -F- * 3 = —4; -, *! + * 2 + x4 = {ί + χ5 = 3; xf> 0, j = lf2f …, 5.
Заполните исходную таблицу симплекса (таблица 0). 「—DS | -2 * 2 2 *! -3 * 2 Все отличия Зы-с ^ Включено в таблицу. 0 Не положительное, но основное решение Х0 = (0,0-4, 1, 1) Допустимо. Поэтому процесс Расчеты, начинающиеся с Второй этап толерантность # 3 = Итак, первая строка = –4. Решать Столбец минимального разрешения амбивалентность:
Таблица 0 1 1 2 3 14 В L8 почвы 0 0 0 зеленый -4 ι1 3 1 в -Ι -Ι 2 О 1 | -Ну 2 в -2 1 -3 -2 0 Любовь | ι 0 0 0 A < 0 1 0 0 1 в Me ° 1 О нас | О нас | О нас | мм J r * i; <°> x4 = Минимум (; ri; = r) = b г! -ci ^ 2-4. Как можно меньше, потому что оба отношения одинаковы Возьмите второе, например. Тогда элемент разрешения равен x12 = = -2. Таблица преобразования. 0, получите таблицу. 1.
Дальнейшие расчеты Включено в таблицу. 2. Получено оптимальное решение XonT = l-g g *. J с 0, O .- ^ -значениями Линейная форма minZ = 4. Как видно из метода двойного симплекса Кроме того, полезно решить проблему линейных целочисленных программ Информация.
Смотрите также:
| Основные теоремы теории двойственности | Транспортная задача линейного программирования и методы ее решения |
| Экономическая интерпретация основной и двойственной задач | Общая транспортная задача |

