Алгоритм симплексного метода

Алгоритм симплексного метода

• Симплексный алгоритм Теорема, доказанная в § 2, имеет вид Действительное базовое решение для получения последовательностей Это заканчивается основным решением проблемы. Симплекс-метод состоит из двух частей: симплекс Метод естественного базиса (симплекс-алгоритм) И симплекс-метод на искусственной основе.

• Прежде чем вы решите Задача линейного программирования симплекс-методом Должен быть создан в стандартном формате. Потом решил Актуальность проблемы решения с помощью симплексного алгоритма Метод. Решение проблем с помощью симплексного алгоритма Начните с известного действующего справочного плана, Соответствует единому стандарту.

В связи с этим его можно сформулировать Два признака удобства, которые абсолютно эквивалентны. Людмила Фирмаль

Решение линейных задач с помощью симплексного алгоритма: 1) Рекомендуется решить задачу по симплексному алгоритму. Для стандартных базовых матриц ограничений один метод По крайней мере, отличается в форме записи Единичный вектор, который может формировать единичную матрицу 2-й порядок; 2) Рекомендуется решить задачу с помощью алгоритма.

Симплексный метод, каждое из его основных ограничений Стандартные формы записи включают Коэффициент g +1 включен только в этот предел. Следовательно, Xo = (x «r, η8 8, …, xs m) -оригинал Приемлемые базовые решения для задач на основе единиц A ^, …, AS / ll, формат модели задачи Ζ = ΣCjXf- * min; xSi + Σa ^ x (= aif i = 1, 2, …, m, 40 * /> 0, l = 1,2 л; при> 0; ί = 1/2 м.

Из математической модели задачи это приемлемо Основа решения Хо базисная переменная равных прав Часть соответствующего ограничения, т. Е. L; ° = α, (ί = 1, 2, …, m). Сам симплекс-алгоритм является вычислительным процессом Такое известное приемлемое оптимальное решение Базовое решение, X0 = (xSl = ax \ xSt = α2; …; xSfn = at).

Как уже известно, для X0 исследования по оптимальности Все векторы Λ / (/ = 1, 2 n) должны быть расширены Вычислить базисные векторы ASL, Asv …, ASfn и разность Z, -C / = Aj. X / вектор, состоящий из координаты A / Исходя из этого, то есть X / = (x1, q2 / …, xmj). Это очевидно Xj — это Oii (ί = 1, 2 м; jf = 1, 2, …, м). Продолжать представлять процедуру расчета Симплексный метод для удобного сокращения исходных данных И характеристики Основные решения доступны в Называется симплекс симплекс стол Таблица.

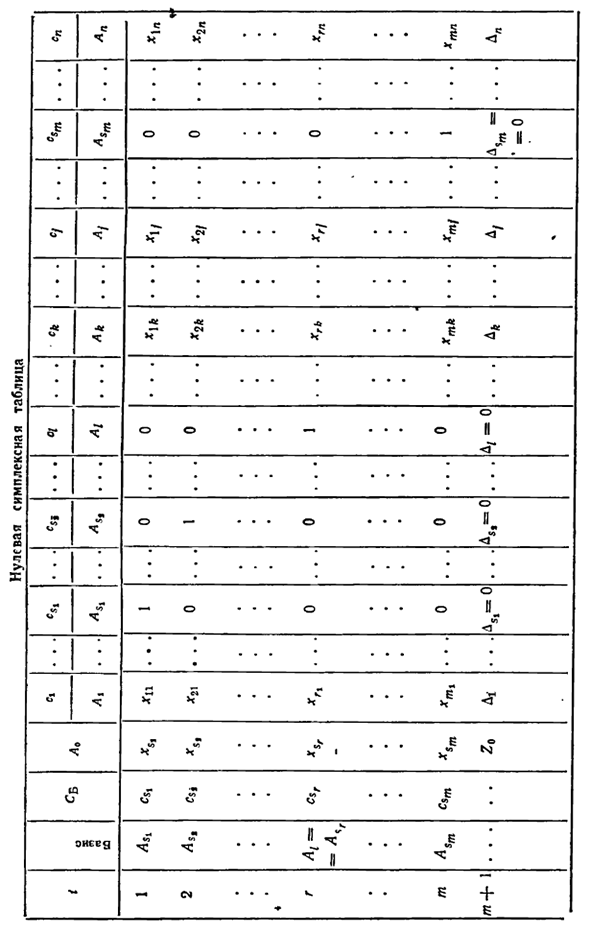
Структура этой вкладки — \ C I Хорошо выглядеть от Ее следующая схема Изображение. Записанная информация Исходное задание Получить симплекс стол Называется источник или Симплекс ноль Таблица. Симплексная таблица вводится в следующем порядке: Строки пронумерованы (столбец i) — записаны * целевые коэффициенты Функция (верхняя строка) -> основы экспортируются (столбец Basic).

Коэффициенты объективной функции экспортируются, Соответствует базовому вектору (столбец грунта) — * компонент экспортируется Разрешенные основные решения (т.е. правая часть столбца Ao) -> Системная матрица экспортируется (столбец Ait A2, …> Ln). так Поэтому сначала введите в первые t строк таблицы, а затем — Последний, то есть t + 1 строка таблицы.

В этом случае столбец Lo Считается нулем, первый столбец (A ), второй столбец (Лг) и т. Д. — для каждого столбца число n (Л „) — до нуля m + + 1 линейное значение в линейной форме Эффективное базовое решение. Это значение Рассчитывается как скалярное произведение векторов Sb и Lo: Значение записывается в последующие ячейки в строке t + 1

Разница Z \ —C \ Z2 — c2, …, Za —βη, они рассчитаны В качестве скалярного произведения векторов Cj и L / мин Соответствующий коэффициент с / целевой функции, т.е. T ζι-ci = Σ ** / C-Cf = SBL / -C /, / = 1,2, …, p. Основные различия, то есть основные различия Если // единичный вектор, вектор всегда равен нулю G единица в / е место, затем SBL / = с / в Чтобы увидеть основные приемлемые решения Смотрите t + 1 для оптимальности.

В то же время они могут встретиться В таких случаях: 1) Все различия Ζ / -С / неположительны (Ζ / -С / <0); 2) Некоторые исправлены / 固定 / -c /> 0 и все Коэффициент π; ・ ・ / <0 (v = 1, 2 м); 3) Есть несколько индексов / Zj-C /> 0, Каждый такой / хотя бы один номер Активно. В первом случае первое действительное базовое решение Оптимальная и минимальная целевая функция Равно равно 0 (теорема из II, 2, 2).

Во втором случае, согласно II, 2, 1 теорема, линейная Форма на множестве L возможных решений задачи не ограничена. В обоих случаях процесс расчета заканчивается там. Наличие третьего случая положительной разности третьего / -q И хотя бы по одному на каждую такую ​​разницу Положительный коэффициент xc является теоремой из ( II, 2, 1) и Аналогичное возможное базовое решение.

Оптимальный и может быть улучшен путем введения его в фундамент Вектор, соответствующий одному из этих различий. кроме Максимально возможное уменьшение значения функции Z = Z0-t (Zj-C /), очевидно, следует ввести Вектор, соответствующий максимуму f (Z / -с, ・). Подумай об определении Очевидные трудности, связанные с вычислением этой величины Практика ограничена более простыми стандартами.

Как вектор, Внесен в фундамент и взят взят Наибольшая положительная разница, то есть самая большая (Z / — ^). В таких случаях Есть некоторые отличия, поэтому вам нужно взять одно из них. Например, меньшее число. Установите max (Ζ / -q) = Ζ * -ck. Тогда вам нужно ввести в фундамент Вектор Ак вместо наименьшего вектора т значение: min — = — и вектор A / следует из базиса.

Xik XRK Новая база состоит из векторов ASi, А8ж, …, ASr_v. Аср. ρ ・ ・ ・ »Асм * Ак. В этом случае XRK называется разрешением (Направление) элемент симплекс таблицы. Столбец (к) И линия (d) на пересечении, где расположен xrk9 Толерантность. Рассчитать новое приемлемое базовое решение, Соответствует полученному фундаменту.

Для этого разлагаются векторы Lo, Au Лг, ..-, недавно записал их Исходное разложение: T A o = Zj XstAsA (1) Ά, = ΣxcA * p / = 1.2η; (2) м Ak = ΣXikA8 £ r (3) Из соотношения (3) выразите вектор A через другие выражения A, ea (A * ~ 2 / * 4 (4) Подставляя формулу результата в (1) Такие, как: A, = Σ (*., — * £ x «) An + ^ = .Σx’s.As. + X’kAk © Поэтому новое приемлемое базовое решение X {= * = (* B AG2 — .., Xn) рассчитывается по следующей формуле.

X1 xSi = Xs £ -jriX £ k ‘ί = 1, 2, .., м; ί = гr (st ・ = / /）; «VFe (6) Χ * = «Rk Аналогично, замена (4) на (2) дает тот же результат, Получите следующее разложение вектора A / с новым базисом. L / = ΣxcAh + xr \ Ak% 1FG где Xij = xz * рк xtk, ί == * ■ 2> ···· m «» ‘^ g. / ^ 1ιΖ 、 ・ ・ ・ ι »Ц / = 1, 2, …, η; i = r. (7) Выведите новую формулу Приемлемые базовые решения.

В отличие от Ζ / — есть Следующее новое решение на основе допусков Повторите формулу: xt = xq — * — Xik, f = 1,2 м + 1; ιφη x \ ^ x_y * «= 0, 1, 2, …, l; (10) n xrk, / = 0, 1, 2 м; i = r. Обратите внимание, что уравнение (10) является нормальным Полная формула исключения для решения системы Линейное уравнение с элементом разложения xgk. Формула (10) Может использоваться для преобразования симплексных таблиц Двумя способами.

Первый способ Руководство (г) Элемент разрешения xrk. С новым симплексным столом Вместо элемента авторизации получается один. Sub Добавьте число k вместо / справа от выражения (10). тогда Мы получаем Xrk Xik = Xik-r-Xik = 0 (ίφΓ). Xrk В результате он будет помещен в новую таблицу Столбец — это единичный вектор, содержащий единицы Рекомендации.

Поэтому оставшиеся строки конвертируются следующим образом: Из оригинальной таблицы симплексных строк Нужно конвертировать, вычесть конвертированный гид, Умножить на этот элемент в этой строке Расположение должно быть нулевым. Второй способ Этот метод отличается Только как получить эти элементы Симплекс таблица, которая не принадлежит Свинцовый провод.

• Чтобы получить один из Такие элементы нового симплекса Требуется таблица из соответствующего пункта Предыдущая таблица охватывает продукты Rie. 9. Скопируйте предыдущую строку в предыдущий элемент Разрешенные столбцы Пункт. Простое изменение второго метода Прямоугольный метод Одна вершина — решить противоположный элемент.

Она является элементом, который должен быть преобразован. 2 других Вершина r элемента стоящего стола Пересечение столбца разрешения и ряда коэффициентов, Элементы для преобразования и стояния на пересечении Это коэффициент столбца и направляющей строки (рисунок 9).

Вместо нового элемента таблицы xc Разница в произведении свинцовых диагональных элементов. Людмила Фирмаль

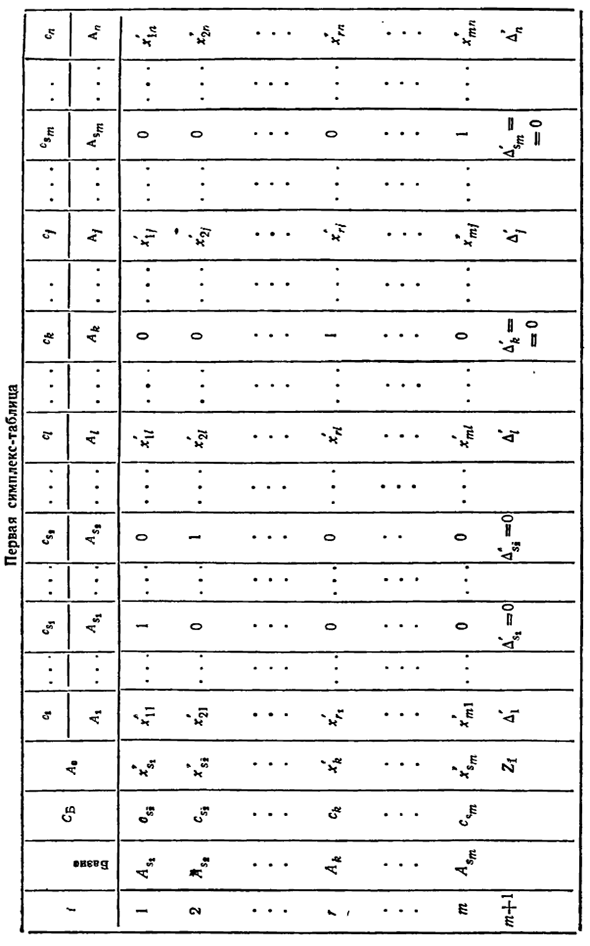
Произведение коэффициента и оставшихся диагональных элементов Разделите на основной фактор. конечно Хгк хгк В результате преобразования нулевой симплексной таблицы Ица Для полной формулы исключения (10) Таблица, содержащая (первую) новую действительную базу Решение.

В этой таблице сделать точно так же, как Источник, то есть (t + 1) -я строка отображается. Для всех Z / -c / <0, Приемлемое базовое решение является лучшим. если Переходите на новый, если положительный в разнице Основное решение. Мы продолжаем процесс до Достигнет или покажет лучшее решение Неограниченный линейный функционал под вопросом.

Пример. Максимальное значение линейной функции Find = 2dG | — ^ 10×2 + 4×3 ~ 6 * 4 — * 2 + 2lg4 <16; xx + 2×2- в условиях 3 * |. * 3 ~ * 2 * 4 ^ * —4; * 2 ​​+ ^ * 3 «- ・ -x4> 0; xt> 0; / 1, 2, 3, 4. Приведите проблему в стандартную форму! —Ζ = -2 *, + 10×2-4X3 4 «6 * 4- * miii; ZX1 ~» * 2 + 2 * 4 + * B = 16ϊ — * 1-2 * 2 + 1-3 + 2 * 4 + x6 = 4; ^ x2-3 * 3 + * 4 + * 7 = 0; Xj> 0; / = 17. Где * 5, * 6, * 7 — дополнительные переменные.

Третье уравнение после Введите переменную * 7, умноженную на минус один. Выписать матрицу Основная система ограничений проблемы A {A2A3ALA5A6A7 (3-1 0 2 1 0 0 \ -1 ^ 2 12 0 10. 0 -1 -1 3 10 0 1 / Единичные векторы AB, L6, A7 составляют основу трех измерений. Пространство (м = 3). Первый симплексный алгоритм решает эту проблему.

Может быть показан Второй симптом приводит к такому же выводу: переменная * 5 «xb> x7, введите только +1 коэффициент для каждого первого коэффициента, Второй и третий пределы. Таким образом, * 5, * 6 и * 7 являются основными. Переменные и т. Д. Не являются базовыми.

Включить неосновные переменные Получить ограничение, равное нулю, первое приемлемое (представленное) основание Решение: xo = (* 1 = ° «x2 = °» xs = °. * 4 = ° «xb = 16» * b == 4. * 7 = 0). Заполните первый симплекс таблицы. Я 1 2 3 1 4 основа A * ζ, — почвы 0 0 0 A0 16 4 4 0 хорошо 1 2 L. 3 -1 0 , 2 левый 10 в -1 -2 -1 -10 Стол -4 ах 0 1 -3 4 6 Al 2 2 1 -6 0 Al 1 0 0 0 ίo A. 0 1 0 0 | 1 A7 0 0 1 О 1

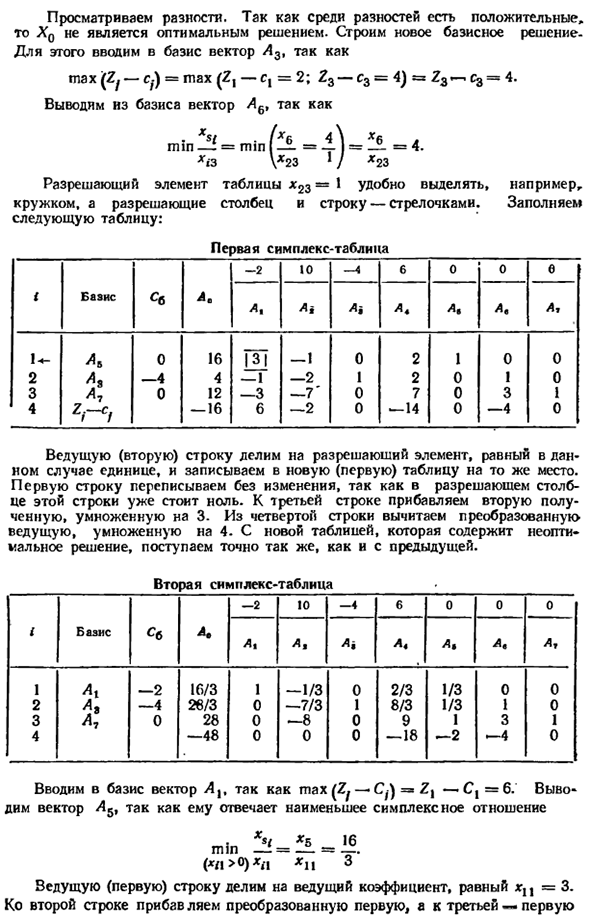
Рассчитать значение целевой функции и разность Ζ, -s. Ζ0 = SBL0 = 0. 16 + 0,4 + 0 ・ 0 = 0; Ζ, -Cj = CB. Л1 ^ с1 = 0-3 + 0 (–1) +0 .0 — (- 2) = 2; # Л2 ^ с2 = СБ.Л2-с2 = 0. (-1) +0. (^ 2) +0 (-1) — (10) = z3-c3 = сб. l3-c3 = ° ・ ° + ° ・ 1 + ° (-3) — (- 4) = 4; Z4-c4 = SBL4- ^ c4 = 0,2 + 0,2 + 0 1-6 = 6; 25-s5 = SBLB ^ c5 = 0,1 + 0-0 + 0,0- ^ = 0; -U; -c6 = SBL6 -sb = 0 .0 + 0.1 + 0-0-0 = 0; -c7 = SBL7-c7 = 0,0 + 0,0 + 0,1—0 = 0. Изучите разницу. Потому что есть положительные различия, В этом случае XQ — не лучшее решение.

Создание нового базового решения По этой причине вектор A3 вводится в базис. max (Ζ, -cL = max (Ζ, -cx = 2; -3-c3 = 4) = Z3— ^ c3 = 4. Выведите вектор A6 из базы. xi3 \ * 23 * / * 23 Элемент решения таблицы x2z- ^ Круги, столбцы и строки-стрелки для разрешения. Следующая таблица: Первый симплекс Например Пожалуйста, заполните Я 2 1 4 основа Zi ~ Cf \ почвы 0 -4 0 A0 16 4 12 -16 -2 Λ, W -3 6 10 Любовь -1 -2 —7 ‘ ~ 2 -4 * ■ 0 1 0 0 6 A * 2 2 7 -14 0 ах 1 0 0 0 0 о 0 1 3 -4 θ1 / U 0 0 1 0

Предыдущая (вторая) строка равна одному решающему элементу В этом случае один пишет в новую (первую) таблицу в том же месте. Перепишите без изменения первой строки следующим образом Столбец в этой строке уже равен нулю. Добавьте вторую строку к третьей строке Получить и тройной. Преобразовано из 4-й строки Лидер, 4х. Использовать новую таблицу с non-opt Наименьшее решение точно такое же, как и предыдущее решение.

Второй симплекс Я 1 2 3 4 основа Αχ почвы -2 -4 0 о 16/3 26/3 28 -48 -2 в 1 0 0 0 10 Ая -1/3 -7/3 -8 0 -4 Любовь о | 1 0 0 6 A4 2/3 8/3 9 -18 0 ах ! / 3 1/3 1 1 2 0 о 0 1 3 -4 0 я A7 0 0 1 0 Поскольку max (Ζ, -С, ·) = Ζχ, вектор Ax вводится в базис -Cx = 6. Поскольку ей соответствует минимальное симплексное соотношение, мы выводим вектор ^ 45 Η Мин- = (* L> °) ** 1 ] 6 3 ‘ Первая (первая) линия делится на главный фактор, равный χιχ = 3.

Добавьте первую строку, преобразованную во вторую строку, и добавьте первую строку в третью строку Будет втрое. То же самое рисуется первым с четвертого. Умножьте на 6. Поскольку все различия во второй таблице не являются положительными, Чтобы получить лучшее решение Hopt = (ψ, 0; ψ, θ); минимум (-Z) = -48; максимум Z = ^ минимум (-Z) = 48

Монотонность и конечность алгоритма. монотонный Алгоритм приводит к каждой итерации Создание нового жизнеспособного базового решения Будьте ближе к лучшему решению. Когда используется строго при решении задач теоремы Алгоритм инструкции, значения после каждой итерации (шага) Целевая функция будет уменьшена.

Доказательство. Положите некоторый симплекс Таблица содержит неоптимально приемлемое базовое решение X Значение линейной формы равно -Z, а разность Z / -С /. Передайте это новому базовому решению X \ и введите это Получено с вектором, соответствующим максимуму (Ζ / .— cj) = Zk- &> 0 в качестве основы.

Наименьший вектор из базы Симплексное соотношение min — = -, т.е. вектор A /. Тогда Χι (* Rt> °) * rt * rk χ Значение функции разрыва равно Ζι = Ζ —— (Ζ & -Ck). χ. Если Zk-ck> 0 и невырожденное решение-> 0, Ζ \ <Ζ. Это означает монотонность алгоритма. С итерацией значение линейной формы ζ уменьшается.

Если проблема вырождена, χι может быть равным Ноль, то Ζ \ = Ζ, что означает строгую монотонность в этом случае , Нарушение Алгоритм конечности. Возможный многогранник возможных решений Задача имеет конечное число вершин (полюсов). Отсюда -Если алгоритм имеет конечное число итераций, вы можете: »Организовать все.

Кроме того, алгоритм сортирует вершины Обеспечивает упорядоченные приближения на каждом шаге Оптимальный пик. В результате Невырожденная задача, симплексный алгоритм строго монотонный, Это конечно. В вырожденном случае, «Петля» гарантирует конечность алгоритма, когда алгоритм потерян Монотонные.

Смотрите также:

Решение задач по линейному программированию

Метод построения допустимых базисных решений	Алгоритм симплексного метода
Отыскание оптимального решения	Основная идея симплексного метода