Оглавление:


Положение центров тяжести фигур сложной формы
- Положение центра тяжести сложных фигур Для определения координат центроида сложной фигуры необходимо использовать методы, описанные в§7.4 и результаты, полученные в§7.5. В
строительстве широко используются стальные изделия различного профиля, все параметры регламентируются ГОСТом, поэтому используются некоторые стандартные профили. Например.
Найдите координаты центра тяжести однородной пластины, показанные на Людмила Фирмаль
рисунке. 7.11 Решение. Нарисуйте координатные оси и разделите площадь пластины на три части. Центроид прямоугольника находится на пересечении диагоналей, а центроид треугольника-на пересечении медианы. Определите координаты центроида каждой
детали: JQ=0,4 / 2=0,2 м, Y1=0,6/2=0,3 м;x2=0,4 + 0,6-1/3 = 0,6 м, Y2=0,3 + 0,3-1/3 =0,4; X3=0,4 + 0,6/2 =0,7 м, U3=0,3 / 2=0,15 м. Найдите площадь детали и всей пластины. LX=0,6-0,4=0, 24М2, А2= 0 ,6″0,3/2 = 0,09 м2, Л3=0,6 * 0,3=0,18 м2, л= 0 ,24 + 0,09 + 0,18 = 0,51 мама. Подставляя
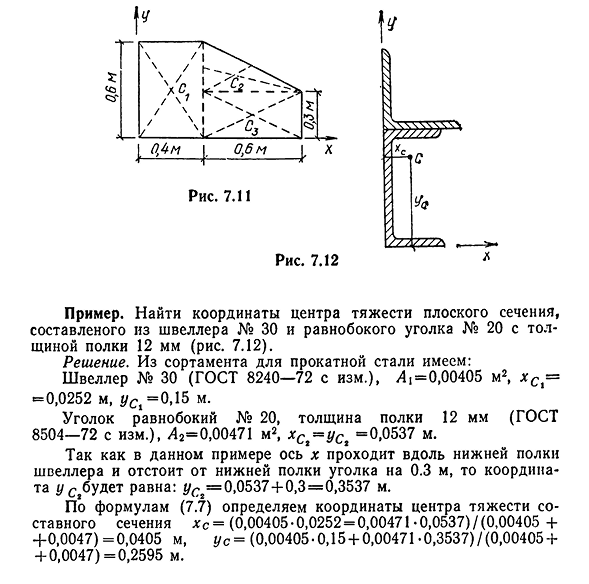
- вычисленное значение в Формулу (7.7), получаем координаты центроида всей пластины.x C— (0,240,2+0,09/06+ +0.18• 0,7)/0,51 = 0,447 m, u s= (0,24 0,3 + 0,09• 0,4 + 0,18 * 0,15)/0,51 = =0,265 м 71-1 7.11 Рис 7.12 Например. Найти координаты центра тяжести плоского участка,
состоящего из канала № 30 и равнобедренного угла № 20 толщины полки 20(фиг. 7.12). Решение. Имейте вне ряд для свернутой стали:канал № 30 (8240-72 с ГОСТ ред.)), L1=0. 00405м2, x C1=e = 0.0252 м, us1=0.15 м. Угловые равные стороны соединяют номером 20,
толщина полки 12мм(Эд и ГОСТ8504-72.), L g=0,00471 м2,^S2=^S2=0,0537 м. В этом Людмила Фирмаль
примере ось x проходит вдоль нижней полки канала и находится на расстоянии 0,3 м от нижней полки угла, поэтому координата y уменьшается до USG=0,0537+0,3=0,3537 м. По формуле (7.7) определите координаты центроида комплексного сечения XC= (0,00405-0,0252 = 0,00471 -0,0537) /(0,00405 + +0,0047) = 0,0405 m, u s= (0,00405 • 0,15 + 0,00471 • 0,3537) / (0,00405 + + 0,0047) =0,2595 м
Смотрите также:
| Устойчивость центрально-сжатых стержней. Общие положения | Устойчивые и неустойчивые формы равновесия |
| Расчет балок на прочность при косом изгибе | Условия равновесия несвободного тела |

