Положение центров тяжести простых геометрических фигур и линий

Положение центров тяжести простых геометрических фигур и линий

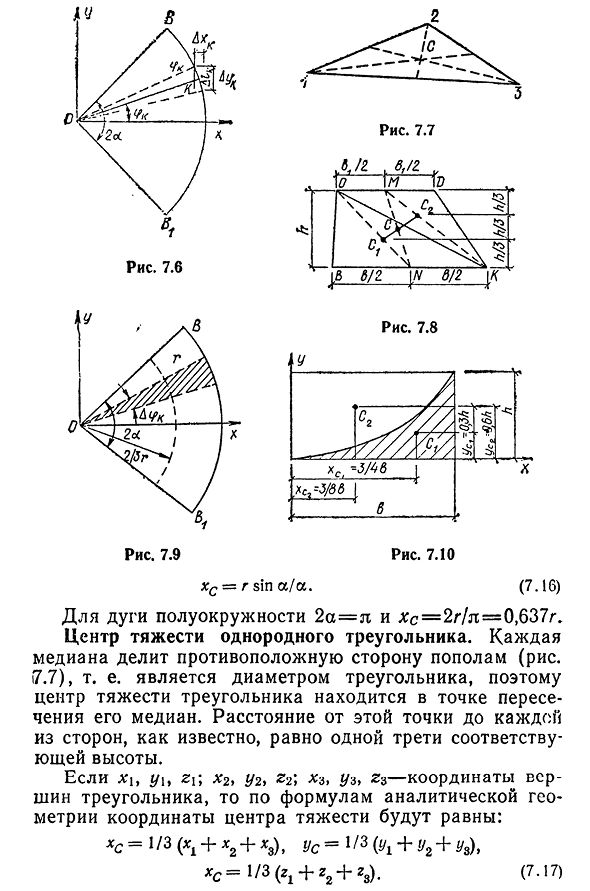
• Положение центра тяжести центра тяжести простой геометрической формы и центра тяжести одномерной дуги линейной окружности. Рассмотрим окружность дуги BB{радиус G центрального угла BOBi=2a. 7.6). Центр тяжести этой дуги находится на оси симметрии через центр окружности и середину дуги.us=0. чтобы найти координаты XC, разделите дугу на бесконечно малые отрезки длины D/A. Таким

образом, координата XL равна xh=R cos по формуле (7.8). я- Из треугольников сторон DX, AUI и D/l формула для D/LSE (RL=DG/A, предыдущая формула принимает вид xc=r^L Ayh^l-rBBJl. Код Учитывая, что/=2ga, BBi=2rsina, мы, наконец, получаем Харрис 7.7 HS-g sin a / a. (7.16) Для дуги полукруга 2a=l и X C=2G / I=0,637 г.

Центр масс однородного треугольника. Каждая медиана делит пополам другую сторону (рис. t7 7), то есть диаметр треугольника, так что центр Людмила Фирмаль

тяжести треугольника находится на пересечении его медианы. Известно, что расстояние от этой точки до каждой стороны составляет одну треть соответствующей высоты. Xi, y\, Z\ \ x2, Uz, z i’, X3, uz, 2Z являются вершинами треугольника координат, если при анализе геометрии по официальным координатам центроида XC=1/3 (1+x2+XS), XC=1/3 (Y1+Y2+Y»)>XC=1/H G1+G2+) 69 однородный параллелограмм центра тяжести. В этом случае центр тяжести

находится на пересечении диагоналей. Частным случаем параллелограмма являются прямоугольник и Квадрат(рис. 7.3, б). Равномерный трапециевидный центр тяжести. Поскольку прямая линия MN, соединяющая середину параллельных сторон ВЧ ОД, является диаметром, то центр тяжести трапеции расположен на ней(рис. 7.8). Разделим трапецию на один к одному, например, ОК, в два треугольника с центром тяжести, лежащим в медиане и км выше в точках Ci и SG соответственно. Итак, центр тяжести трапеции

• должен находиться на линии, соединяющей точки Ci и C2. Тогда пересечение линии C]C2 с диаметром MN будет трапецией и центром тяжести. Расстояние от центра тяжести С до дна трапеции определяется по формуле (7.7). Площадь треугольника ВКР равна Ai=0.5 bh, координаты США, его центр тяжести yct=h!3. Аналогично, для второго треугольника OKD имеет L2=0, 5Y1L,=наконец, мы находим, что центр тяжести находится на линии, соединяющей середину параллельной стороны, на нашем расстоянии от нижнего

основания. BH h b^h2h2 3 N3 Три. Шесть. (I-26,) 6(6+26),) Us-bh2 bt h Б2 h2 (6+6,) 3 ( 6 + 6 , ) ‘ ( 7 ,1 8 ) Центр тяжести однородного кругового сектора. Укажите ось x вдоль оси симметрии сектора WWII с центром окружности радиуса g в качестве начала координат(рис. 7.9). Разделим этот сектор на n равных базовых секторов с центральным углом DSR^. Центр тяжести треугольника находится на его медиане на расстоянии 2 / ZG от точки O,

при этом центр тяжести всех основных секторов расположен в дуге окружности радиуса 2/ZG. Людмила Фирмаль

Таким образом, задача сводилась к определению центра тяжести равномерной дуги окружности радиуса 2 / ZG угла центра 2а. 2 грех x s Мы-0. (7.19) 70 2a для полукруга=l и HS=4 / 73l=0,424 г. Центр масс однородного треугольника параболы. Положение центра тяжести однородного ПА, параболического треугольника(рис. 7.10) как определено следующими координатами, мы дадим их без вывода: xCj= — r / Cj=o, 3 / i;a^b h / 3,3 b rCe=—, r / C t=0,6 / i;A2=2bh / 3. (7.20 утра))

Смотрите также:

Предмет техническая механика 

Расчет балок на жесткость при изгибе	Работа внешних сил
Пределы применимости формулы Эйлера	Построение эпюр изгибающих моментов и поперечных сил при изгибе балки