Оглавление:

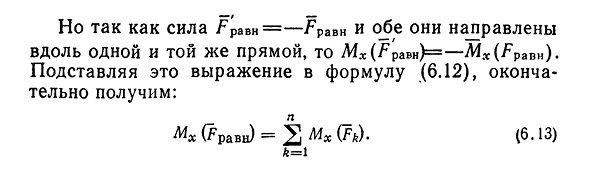

Теорема Вариньона о моменте равнодействующей относительно оси
- Теорема валиньона относительно теоремы оси приводит к мгновенному результату. Если система любой пространственной
силы имеет равнодействующую силу, то ее момент для любой оси будет равен сумме моментов всех
сил для одной и той же оси. Давайте Людмила Фирмаль
убедимся, что любая космическая система доказательства силы действует на твердое тело{Fb F2… …И Fn}. Результирующая линия
действия FpaBH в этой системе проходит через точку B(рис. 6.4). В этот момент f paBii=3 » FpaBH, и система{Fi, F2t…t Fn, FpaBH}находится в
- равновесии и выполняется условие (6.9). В частности, система{Fb сумма моментов всех сил F2… …, Fth FpaBH}для осей координат X
равно: 2L1x(?) y)+MX(g; AV n)=0-(6.12)L=1 Так как же power / 60no?Равный= — / равный, оба направлены вдоль
одной прямой, а затем Mx Людмила Фирмаль
(F’pam)= — Mx (FpaB»). Подставляя это выражение в выражение (6.12), можно, наконец,: M x (Travi)=2MX (Fk). (6.13))
Смотрите также:

