Оглавление:

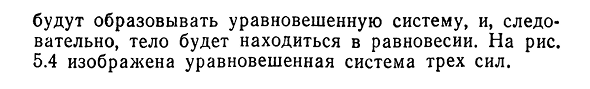

Графическое определение результирующей пары. Графические условия равновесия произвольной плоской системы сил
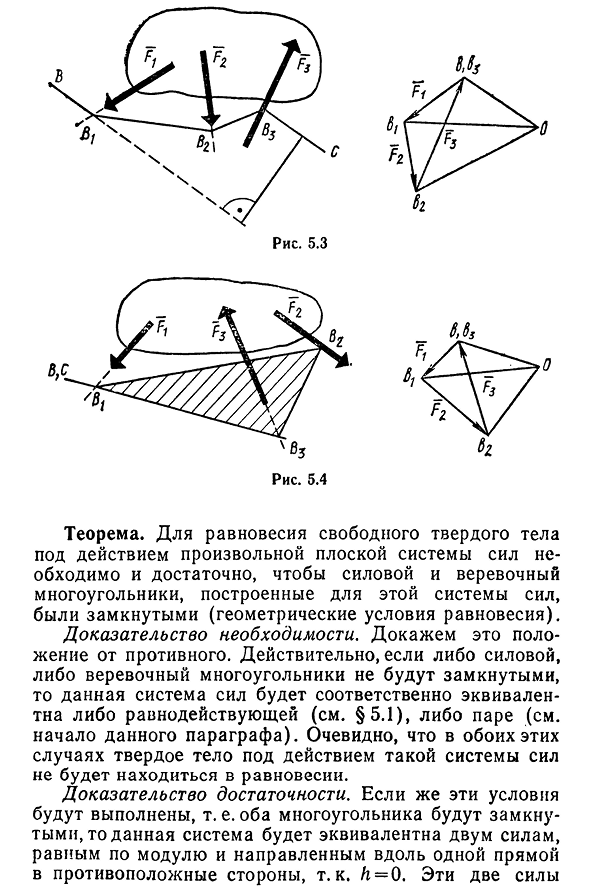
- Графическое определение результирующей пары. Графическое условие равновесного состояния любой плоской системы позволяет любой плоской системе действовать на свободное твердое тело^2, F3.
5.3). Затем, после построения канатного многоугольника в соответствии с вышеприведенным правилом, крайние стороны bbi и B>C остаются параллельными
одной и той же линии o, так что они Людмила Фирмаль
параллельны друг другу, так что пересечения этих сторон находятся на бесконечном расстоянии,и канатные многоугольники не замкнуты. Однако, согласно (5.1), данная система может быть
заменена двумя силами, равными в данном случае h и o, поскольку O3=o, причем вдоль параллельных линий BBi и B3C. {Флорида. ? 2. Fs}о oo (0,) — (5.2) Момент такой пары равен m=Obh. Величина M является главным моментом в системе этой силы и не зависит от выбора точки O. 50% 5.3 Теорема гласит, что для равновесия свободного
- твердого тела под действием любой силовой плоской системы Сила, построенная для этой силовой системы, и канатные многоугольники замкнуты (геометрически). Доказательство необходимости. Докажем это положение с противоположной стороны. На самом
деле, если многоугольник силы или веревки не замкнут, то система этой силы будет эквивалентна результату (см.§5.1) или паре(см. начало этого параграфа). Понятно, что в обоих этих случаях твердое тело под действием системы таких сил не приходит в равновесное состояние. Доказательство адекватности.
Если эти условия выполнены, т. е. оба полигона замкнуты, то эта система равна по Людмила Фирмаль
модулю, потому что y=0, и эти две силы в противоположном направлении. Четыре. Они образуют сбалансированную систему, поэтому организм сбалансирован. Для риса. 5.4 показаны три силы системы баланса.
Смотрите также:

