Сравнение бесконечно больших функций

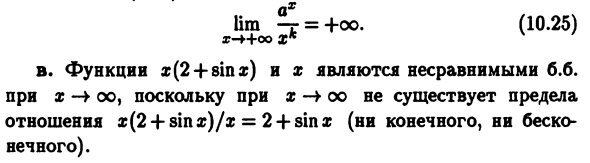
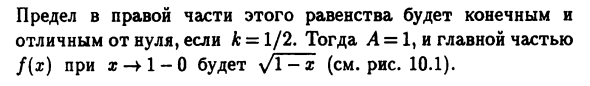
Сравнение бесконечно больших функций

• функция bb, можно ввести классификацию, Аналогичные функции, связанные с функциями (см. 10.1) Со своими личными ограничениями. Пусть v (x) и w (x) — функции. как x- + a (см. определение 7.11), где a конечно или Бесконечное число расширенных числовых линий. iim v (x) / w (x) = c € R \ {0}, если присутствует х— ¥ а Случаи v (x) и w (x) называются b.b. Одна функция порядок как x- * a и v (x) x = aO (w (x)) или w (x) x = aO (v (x)). Если c = 0, v (x) называется b.b. Функция низкого порядка роста по сравнению с w (x) 14c и v (x) x = ao (w (x)) описаны и бесконечны

Отношение v (x) / w (x) -b.b ограничение с функцией Более высокий рост по сравнению с ишемическим w (x) Напишите b) (x) x = ao (v (x)) (слово «рост ** часто опускается»). Наконец, если нет ни бесконечного, ни конечного Это ограничение отношений, v (x) и w (x) называются x-> Функция, которую нельзя сравнить с bb. Пример 10.9 а. Функции 2×2 и x2 + x являются b.b. в том же порядке, что и x- \ oo Iim — = — = Гм, x- * oo x1 + X a? -фу 1 4 » б. Функция ax (a> 1) является b.b. выше Порядок роста по сравнению с xk (k> 0) при x-> + oo (7,32) о Iim -r = 4-оо. (10.25) x — ++ oo X * с.

Функции s (2 + sinx) и x не имеют себе равных b.b. х- \ оо, как; -> без ограничений Людмила Фирмаль

Отношение а: (2 + sinx) / x = 2 + sinx (если не конечно) Бесконечность). Определение 10.6. Функция v (x) называется b.b. к-й Порядок по w (x) равен x = a, а число k равно Функция rldcom bb v (x) имеет вид x-> a относительно w (x) 1 порядок, когда функции v (x) и wk (x) являются b.b а, если Lim-4? m = c∈R \ {0}. (10.26) bm — функция, функция заказа до 1 bb По сравнению с другим 6.6. Функция не является обязательной Если порядок положительных чисел и функций v (x) относительно w (x) равно & тогда порядок функции v (x) равен «v (x) равно л / к. Не обязательно bb-функция v (x), эквивалентная В каждой степени WK (х), может быть ясно показано Заказать к. Следовательно, функция ax (a> 1) эквивалентна x- * + °°.

Порядок во всех степенях xk (k> 0), но в порядке (10.25) От x до \ + oo рост этой функции на x невозможен. Определение 10.7 Функции Bb v (x) и w (x) как x- + a Когда он называется эквивалентным и указывает от v (x) x до aw (x) предел их отношения в х- \ а равен единице, или 1. (U.27) Функция, эквивалентность как в б.м. Работает симметрично и транзитивно. Заявление 10.1. Функция ограничения отношения 2 bb Равен пределу эквивалентных отношений. В качестве конечного числа функции стригущего лишая x → ∞ Для каждого термина можно указать порядок роста Для х, члены более высокого порядка ( Только) называется основной частью суммы b.b. х- * оо Функция. Следовательно, многочлен степени n Pn (x) = aohp + ahx «-1 + … + an ^ x + an (a ^ φ0)

• Это сумма 6,6. как x- * oo функции, то порядок Рост k для каждого члена x Связанный индекс. Поэтому термин oqx71 Более высокий порядок роста (k = n), потому что он уникален, и х- * оо будет основной частью этого общего. Как хорошо Функция X для суммы конечного числа bb — ► может Показать порядок роста для каждого термина Для l / (x-a) члены высшего порядка также в основном Для этого раздела часть такой суммы в х-та Единственное. Например, всего l / sin2z + ctgx две функции bb Согласно x-> 0 (10.18) первое слагаемое является квадратичным. По отношению к 1 / х второй является первичным. так Основная часть этой суммы при x-> 0 равна l / sin2x.

Заявление 10.2.В общем, мы можем говорить о основной части, но не Только конечная алгебраическая сумма x-ba (или х — ► ° °) как функция, а также любая функция в структуре Эквивалент f (x), x-> a и степенной функции A / (x-a) k (X- * оо-степенная функция Axk), AΦ0, k> 0. Степенная функция и основная часть будут 6,6. функция Как x-> a или x-> oo соответственно. Как найти Коэффициент A и индекс k основаны на Использует определение 10.7 и утверждение 10.2 и аналогично процедуре Функция назначения основной части bm.

Итоговое количество полных функций Это соответствует основной части. Людмила Фирмаль

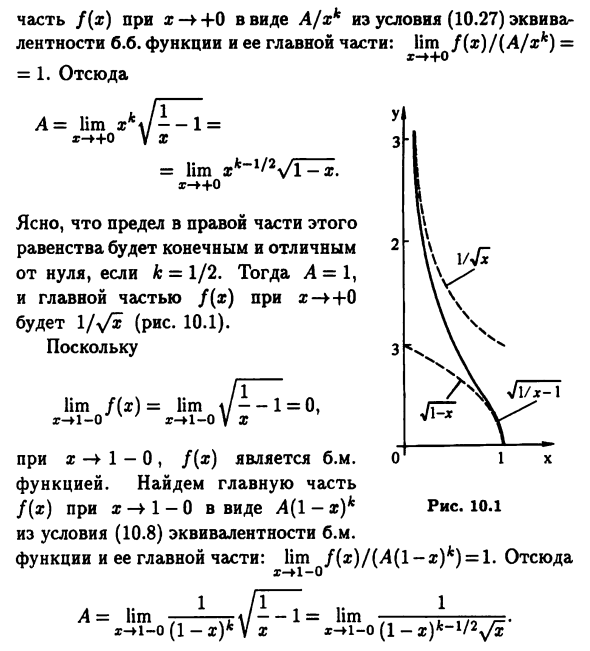
Пример 10.10. Функция f (x) = y / l / x-1 имеет вид Полуинтервал (0, 1) и как базовая функция непрерывна На этом интервале (см. 3.6 и 9.5). с того времени lim f (x) = lim \ -1 = +00, x — ++ 0 s- * + 0 V X как x —► +0 Эта функция bp, строка a: = 0 Вертикальная асимптота графа f (x). Найти основную часть f (x) при x — ++ 0 в виде A / xk из условия (10.27) Функция эквивалентности и ее основная часть: lim f (x) / (A / xk) = = 1 = Оправа О ag — ++ -X. Очевидно, это правильный предел Равенство конечно и отлично С нуля, если к = 1/2. Тогда А = 1 И х — »+ 0 в качестве основной части ф (х) \ jyfx (рисунок 10.1). с того времени im Dx) = lim \ -1 = 0 I-O V ‘Z-N-O V х ободок a: -> 1-0, f (x) — b.m. Я Функция. Найти основную часть f (x) при x -4 1-0 Формат A (1-g) * Из условия эквивалентности b.m. (10.8) Функция и ее основная часть: lim f (x) / (A (l-x) k) = 1 Рисунок 10.1 1/1, .. 1 n = hm yr \ / -1 = lim -r— от r-fi-o (1-x) до V x z-n-o (1-а 🙂 * «1 Правая граница этого уравнения конечна, Ненулевое, когда k = 1/2. Тогда A = 1, а основная часть f (x) при x -4 1-0 — это y / 1-x (см. рисунок 10.1).

Смотрите также:

Предмет математика

Эквивалентные бесконечно малые функции	Наклонная асимптота графика функции
Главная часть бесконечно малой функции	Общие рекомендации по вычислению пределов