Оглавление:


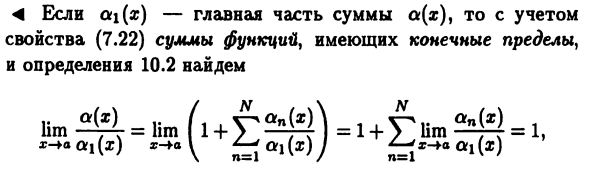



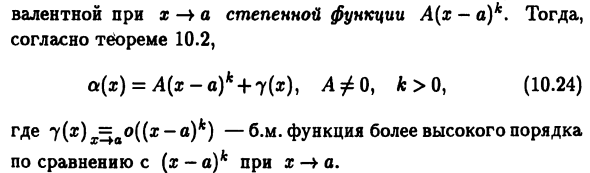



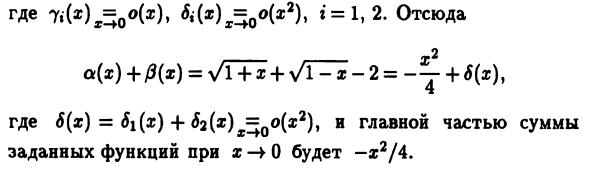

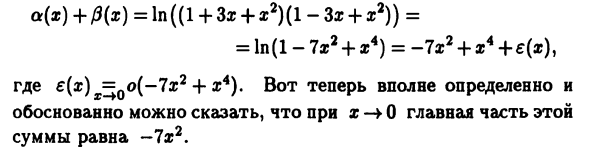

Главная часть бесконечно малой функции
- Согласно утверждению 7.4, сумма конечного числа функций Днем Ж4с, опять же как Б.М. х- \ функция. Дай мне an (g), n = 1, N, -b.m. x- + a, функции u и a (x) имеют вид Сумма. При n = 2, если Noin (x) x ^ ao (ai (x)) ^, ai (s) называется основной частью общего bm функций x- \ a. ли Это термин по основной части суммы Th и b.m. Маленький заказ по сравнению друг с другом Срок действия. Понятно, что у общего числа есть бесподобное добавление (См. Определение 10.3), основная часть не может быть отделена. Пример 10.5 Итого s \ nx + \ n (1 + x2) + $ / x б.м. х- ¥ 0 функции, следует учитывать, основная часть будет у / х (10.18) и теорема 10.4 грехи x ln (l + s2) x2 urn -r = r = urn -77 = = 0 и lim — * — r = — = lim -r = = 0, х-э-э-э-э-э-э-э-40 Это sinxx = o (ffi) и ln (l + s2) = Qo (f / x) Определение 10.2. #
За каждый семестр в общей сложности b.m с x- + a Функция, вы можете указать порядок k относительно x -a, основной Часть этой суммы будет периодом (если это единственный период) Низкий заказ. Общая численность х.м.н.о. как основная функция Часть представляет собой младший член по отношению к 1 / хТеорема 10.5. Итоговое итоговое число б.м. х-т Эквивалент его основной части, или N Vn = V / Van {x) x = ao (ax (x)) = ► a (x) =] Pan () x3e < i (*). n = l <Откуда (х) — основная часть суммы а (х), тогда рассмотрим Полные свойства функций с конечными пределами (7.22), И определение 10.2. Согласно (10.8), х- \ а Функция Б.М. и ее основная часть. ►
Это единственный и для каждого Условия могут быть в порядке возрастания. Людмила Фирмаль
Натуральный Юл. В каком-то панк-районе о U (a) относится к сумме конечного числа b.m. как х-> п функция Оставьте свой главный знак или n = 1 = ►3U (a): Vs € U (a) ^ Щ> 0. (10.23) 4 В процессе доказательства теоремы 10.5 x-> a a (z) / ai (z) -4 1. Из свойства функции с in Хранить в точке a, ненулевой конечный предел В некоторых проколотых окрестностях этой точки есть предельные символы, Следуйте (10.23). ► Пример 10.6 а. Рассчитать .. г / х + гм Хмм х- + о грех с того времени Hm mt = lim v ^ «= 0 и Hm -mt = Hm Vx * = 0, 「-►Оуr-fO r- + 0 ^ ааг-Ю Затем, согласно (10.3), y / xx = Qo (^ x) и ^ X5 °° (^^ * Дробный числитель под символом предела — это bm x-> 0 Согласно теореме 10.5 функция ^ x эквивалентна. Если x- ¥ 0, вся молекула. (10.18) и из теоремы 10.3 sinffix ~ otfx. Таким образом, как числитель, так и знаменатель Это эквивалентно тому же b.m. х — ►
0 функция как ^ г, То есть согласно (10.9) они эквивалентны друг другу при x-> 0, По определению, обязательный лимит составляет 10,5. Найду .. 1-СО8Ж + 23 гм :. ху арксин Дробный числитель под знаком предела является суммой двух В случае 2-> 0 вечера функции 2x и 1-cosx = 2sin2 (x / 2). главный Из примера 10.2.a, 2hu будет частью этой суммы. То есть 2sin2 (s / 2) = o (2x). (10.18) по arcsins ~ nx. Заменить дробный числитель и знаменатель на эквиваленты x-> 0 м. Функции 2x и x соответственно Это ограничение 2. с. Рассчитать гм а: 3) Числитель дроби ниже предельного символа является алгебраическим Всего в 3 часа дня плюс x-0 как функция 0, x4 = o (x) и Smxx = QO (x) и tgxx = QO (x), согласно (10.5), (10.8), (10.18) То есть порядок двух слагаемых одинаков (первый) Относительно х.
- В этом случае необходимо разделить итоговую сумму b.m. Это работает, чтобы подчеркнуть свою основную часть. от Учитывая пример 10.3 (10.8), tgx -sins ~ a? 3/2 рядом, Теорема 10.5, дробные числители под предельным знаком эквивалентны В случае x-tO во второй половине дня функция x3 / 2, потому что x4 = o (x3 / 2). Know (10.18) и теорема 10.3, переключатель дроби х-> 0 м. функция g3. В результате этот предел составляет 1/2. # В общем, мы можем говорить о основной части, но не Только алгебраическая сумма a (x) конечного числа b.m. Когда x- ¥ a Произвольная структура функции a (x), а не только функции x- »a Эквивалент степенной функции A (x-a) k. тогда Согласно теореме 10.2. a (i) = D (x-a) * + 7 (*), A # 0, k> 0, (10.24) Где y (x) x = ao ((x-a) k) -b.m. Сравните с (x-a) k как x-> a
У нас есть это выражение Функция a (x) в форме (10.24) уникальна. на самом деле Если выражение а (х) было возможно с ним- = £ (x-a) m + <* (a;) где B # 0, m> 0 и S (x) x = ao ((x-a) m), Согласно теореме 10.2. Это возможно с (10.8) только для B-A и m = k. Процедура разделения основных частей в формате A (x-a) k Во второй половине дня как x- + функция a (x) связана с учетом ограничений ободок A (h-a) ~ И выбор значений K и A, этот предел Оказалось равным 1.
Степенная функция A (x-a) * является основной частью b.m. х- \ а, функция а (х). Людмила Фирмаль
Выделив основную часть, вы можете: Используется для приблизительного расчета значений Функция а (х) для значения х вблизи точки а. Результат абсолютный \ h (x) \ и относительный \ h (x) / a (x) \ Ошибки имеют тенденцию быть нулевыми в x-4a. Стригущий лишай требует более высокой точности расчета значение или представление (х) в окрестности а, Затем Б.М. Основная часть должна быть отделена от в х-) ■ -> A функции y (x). Вы можете продолжить эту процедуру. такой Процедура улучшения называется строительством Асимптотическое разложение функции вблизи заданной точки. Пример 10.7 Точность замены на s = (10.17) = = 1/2 и 140 функций \ / 1 + х -1 Вт / 2 на функцию Не достаточно
Отличить от функции 7 (s) = xL + x-1-x / 2 Выберите A и k из условий и часть формата Ahk Для этого конвертируем: 24-644 + х / 2) 2 -х2 / 4 Вы можете легко увидеть, что f (x) x ~ 0-x2 / 8. Следовательно, А = -1/8 и к = 2. После этого X2 Где <((π) x5 ° 0 (x2). Если вам нужно сделать его выше После подтверждения точности выберите основную часть из m. x — ► Функция 6 (x) как 0 # 2 для bm как x- * a функций a (x) и p (x) Их основными частями являются A (x-a) k и J3 (x-a) m соответственно Что вы можете сказать о основной части суммы a (x) + / 3 (x)? С KFT основная часть суммы будет частью термина A (x-a) k и B (x-a) m. Индекс меньше, чем этот. Если k = m, основная часть суммы равна (A4-B) (x-a) k Для А + В ^ 0. В противном случае основной
Часть слагаемого взаимно уничтожается, общее а (х) + / 3 (х) х-> б.м. получается. Функция высшего порядка Чем каждый срок. В этом случае вам нужно выбрать Тогда функция вида C (x-a) 9 при q> k. Пример 10.8 а. Функция a (x) = y / T + H-1 и p (x) = = y / \ -x -1 это b.m. Как х- * 0. Пример 10.7 x as- ¥ 0 7 | (*) i = 0). ^ MF = OF2), t = 1,2. Отсюда Yao a (x) + 0 (x) = y / T + i; + y / Ti; 2 Где ^ (x) = ^ i (x) + ^ 2 (^) x = of2), а основная часть суммы Функция, заданная как x-> 0, равна -x2 / 4. б. Где функция a (x) = 1n (1 + 3x + x2) и /? (Х) = 1n (1-3a + x2), м.м. Как х-> 0. С (10.18) Учитывая теорему 10.3, In (1 + 3s + x2) ^ 3s + x * и In (1-3s + x2) x до Q-3s + x2. Теперь мы можем сказать, что основная часть количества og (x) + β (x) x-> 0 становится 2×2. Но такой вывод Поскольку это поспешно и поверхностно, это часто бывает, Я ошибаюсь Дело в том, что это только следует непосредственно из (10.18)
Эквивалент ln (l + z) 2JO *> т.е. согласно теореме 10.2. Обозначения 1n (1 + r) = z + y (z). Где y (z) = o (z). к На основании теоремы 10.3 положим z равным 3x + x2 или -Ж + З2, тогда Ln (1-3l + x2) = -3l + l2 + 62 (w). Где ^ 1 (x) x = 0 ° (3xH-x2) и k2 (x) x = Qo (-3x + x2). позже Получить дополнительную функцию данного б.м. Но последние два условия справа сами по себе Содержит форму Ax2 термин, необходимый для входа в основной Часть суммы a (x) + / 3 (x) при x-> 0 Основная часть суммы оригинала б.м. Будь добр + 3л + 2) (1-3л + 2)) = Где e (x) x = Qo (-7×2 + x4). Теперь определенно и Если x-> 0, эту основную часть можно назвать разумной. Сумма равна –7g2. 24 *
Смотрите также:
| Сравнение бесконечно малых функций | Сравнение бесконечно больших функций |
| Эквивалентные бесконечно малые функции | Наклонная асимптота графика функции |

