Оглавление:





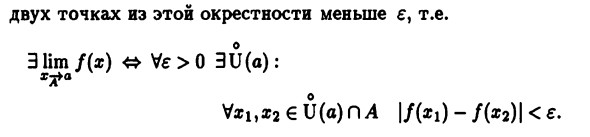




Признаки существования предела действительной функции
- Теорема 8.15. Для x-ga} (x) 0, такой / (X) -6 | ni Ах ах Проколотые окрестности U (a) и Ui (a) из условия Ах ах U1 (a) СU (a), неравенство Пример 8.3 Функция 1 / x2 и arctan (l / x2) Vx € A = R \ {0} Оно не уменьшается как х- »0. Теорема 8.16. Для x-ga функция f (x) не уменьшается (Или не увеличивать), ограниченный сверху (снизу каждый) существует как х-> 0 = sup (/ (x): xe И он конечен. Свяжите 0 и 3Ui (o) = Ах ах A: 0 6, тогда неубывающая функция с определением 8.5 и точная топ > sup {/ (x): x e (U (a) \ Ui (a)) АA} £ / (π)> 6-й. Ах ах В то же время, от Ui (а) СU (а) sup {f (s): x∈Ui (a) n4J a Обеспечьте t-> a и ограниченность из -f (x) выше. как Только что доказал Hm (- / (aO) = sup {- / (s): так Другими словами, описание теоремы применимо, даже если оно не увеличивается Функция. ►
Теорема 8.17. <Не уменьшайте функцию f (x). Произвольная о Поскольку в проколотой окрестности U имеется значительное число M из (a) точек xm, С вершины функции f (xm)> M. Найти такой проколотый район. 0 0 U a (a), x * e Ui (a) ⊂ U (a) и так далее. Тогда дано Определение 8.5 M ^ sup M, (8.7) дает lim f (x) = +00. Ход доказательств, когда не растет и Функция x-ga неограничена следующим образом. ►
Бели} (x) с использованием функции x-ga не уменьшается (Или не увеличивается), не ограничены (соответственно Снизу) тогда lim f (x) = + oo (lim f (x) = -∞ соответственно). Людмила Фирмаль
Из того, что было рассмотрено в примере 8.3, оно не уменьшается при x-> 0 Функция (A = R \ {0}) сначала не ограничена, Для этого И »z = + оо. (8-19) Кроме того, второй ограничен 1 7G limarctg-r = -. (8,20) х ° х 2 Теорема 8.18. Ограничение функций). Функция f (x) является x-> конечной Ограничить, только если положительный о Существует проколотая окрестность U (a) в точке e Абсолютное значение разницы между значениями любой функции Две точки из этой окрестности меньше е, то есть 3Hm / («) <» te> 0 3U (a): х-ФИА
Сначала примите, что есть предел, и покажите его B. И благодаря (8.5) для ε> 0 о проколотая окрестность U (a) такая, что \ f (x) -b \ 0, удерживайте (8,21). Получить последовательность {& „} для точки xn £ A Метрическое пространство А к точке а. тогда Согласно определению 8.2, начиная с номера N + 1, все Элементы этой последовательности попадают в эту Район. так Ve> 0 3N (e) € N: (n> N) A (m> N) => | / (xy) — / (* x) | + Ко. Указывает, что f (x) равномерно непрерывен. L. f (x) Теорема 8.16 означает, что x-> + oo конечно. Ограничить.
Это, в свою очередь, благодаря стандарту Коши (теорема 8.18) 3U (+ оо): Vxux2 € U (+ оо) nA \ f (xi) -f (x2) \ Бесконечный прокол окрестности + оо расширение Числовая линия совпадает с окрестностью этой точки. о U (+ oo) = {x € R: x> E} VE € R. Особенности у нас есть Yy> 0 e> d: Vxux2> E \ J (xx) -f (x2) \ 0 также может быть \ x \ -x2 \
Смотрите также:
| Некоторые свойства предела отображения | Непрерывность функции в точке |
| Пределы действительных функций | Свойства функций, непрерывных в точке |

