Оглавление:

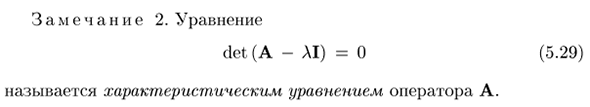

Характеристический многочлен линейного оператора
- Характеристический полином линейного оператора. Пусть A линейный оператор, а I тождественный оператор L (V, V). Полином для определения A дет (A- E.25) Это называется характеристическим полиномом А.
- Базис {e ^} задан в пространстве V, а матрица A = (a ^). Оператор А основан на этом. Тогда согласно E.24) Полином А.25 оператора А записывается в виде задолженности (A -AI) = — < о ( о A2- a1 L стр a1 … вверх L E.26)
Напишите характеристический полином E.25), обозначенный dk Коэффициент AFE дет (A-AI) = E.27) Людмила Фирмаль
- Примечания 1. Значение определителя det (A-AI) равно В зависимости от выбора основы, коэффициент характеристики dk Полином в правой части E.27 также не зависит от выбора базиса. Следовательно, коэффициент dk характеристического полинома Инвариант оператора A-количество, значение.
Это не зависит от выбора фонда. В частности, коэффициент dn- \ явно равен a \ — \ — a \ — \ -…- \ -a ™ является инвариантом. Этот инвариант Далее следует оператор A, обозначенный символом tr A (от англ.) Word trace-trace): trA = a \ + a \ + … + a ™. E.28) Замечание 2: уравнение дет (A-AI) = 0 E.29)
Называется характеристическим уравнением А Людмила Фирмаль
Смотрите также:

