Понятие числовой последовательности

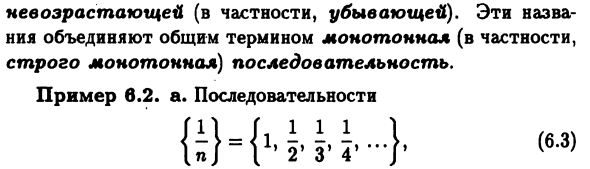
Понятие числовой последовательности

• Многие номера принимаются Переменная i может быть упорядочена по присваиванию (см. 2.6). Каждое значение имеет определенный серийный номер: я, х <я, …, xn) …, затем получить числовую последовательность Значение переменной x в порядке Увеличьте число n. Когда m = n + 1 элемент Последовательность xm называется следующей e & xn, где xn Предыдущий xt. Белый n = 1, 7В, т.е. вы можете указать Последний элемент последовательности HDG называется почкой. Белый последний элемент не может быть указан. n € 14, такая числовая последовательность называется Бесконечен и указывает {xn} (для краткости Бесконечная последовательность чисел называется просто Последовательность).

С алгоритмом расчета Он отражает процесс непрерывного приближения Целевое решение и физические измерения Различные значения или параметры технического объекта С различной точностью последовательности Результат характеризуется близостью к истинному значению. Поэтому важность изучения свойств Последовательность. С довольно распространенной позиции последовательность Рассматривается как образ множества N натуральных чисел Его отображение f: N-> R в реальное множество R

Последовательность удобна и относительно Простая модель переменных-основной Математический анализ людей. Людмила Фирмаль

Числа. Это отображение на каждое натуральное число n € N Установить в соответствии с указанными правилами / только номер xn =} {n) G R, n € N. (6.1) Элемент последовательности Разные точки множества R. Этот факт Свести концепцию последовательности к концепции Счетное подмножество множества R (см. A.2.1). так И € R является фиксированным числом, последовательность x \ = a, «2 = o, …, xn = a, …, это называется константой, Это не то же самое, что один элемент a e R. В этом случае Бесконечное число элементов последовательности Этот набор значений содержит только один элемент. Если принадлежит, последовательность считается заданной Правило / можно найти любой элемент xn Его номер р.

Это правило может быть указано в выражении (6.1) В случае так называемых общих терминов для последовательностей, установить зависимость от n (например, элемент Арифметическое sn = a + (n-l) (f и геометрическое xn = bqn ~ 1 Прогрессия (a, d, byq 6 R); ряд чисел xn = 1 / n, Обратная природа). Тем не менее, HP может быть установлен Повторите формулу. Выражено с предыдущим элементом. Например, последовательность {xn} = {n! } Этаж Общий термин xn = n \ Vn € N также определяется как: x \ = 1, xn = nn_1 Vn <= N \ {l}. Пример с.1. Вы можете установить повторное выражение Последовательность Фибоначчи: * 1 = * 2 = 1, sn = * n-i + * n-2 Vn € N \ {l, 2}, (6.2)

• Назван в честь итальянского математика Леонардо Пи Внес Занский (Фибоначчи) (1180-1240) Европейское проникновение арабских достижений в математике. Эта последовательность связана с ним Общеизвестная задача разведения популяции кроликов: каждая пара Взрослый кролик приносит самку и самца каждый месяц, Я рожаю через два месяца после рождения. Сколько Пара кроликов будет 1 год, если их было 1 в начале года Пара новорожденных кроликов, и никто не умер в течение года. Найти приложения в последовательности Фибоначчи (часто неожиданно)

Различные разделы математики. Определение 6.1. Стригущий лишай последовательности {xn} Неравенство xn sn + i) Vn∈N Называется неубывающим (особенно возрастающим) Не увеличивается (особенно уменьшается). эти Пример 6.2 а. последовательность Строго монотонный, (6.3) уменьшается, (6.4) Это увеличивается. б. {1, 1, 2, 3, 5, 5, 8, 13, …} последовательность чисел Фибоначчи (см. Пример 6.1) монотонны и не уменьшаются. с. последовательность (-1) M_G 3 13 11 \ ^ / -Г’2’3’4’5’2 ‘»Т (65) f ^ lTnl / 1 2 3 4 5 | \ n + 1 / \ 2’3 ‘4’ 5 ‘b1’ «J [} Это не однообразно. Определение 6.2. Последовательность {xn} называется Ограничения применяются, если можно указать положительное число М.

Название является общим однообразным термином (особенно Строго монотонная) последовательность. Людмила Фирмаль

Не превышайте абсолютное значение Элемент xn этой последовательности, т.е. ЗМ> О: Vn € N | хп | 0 3n € N: | wn |> M, Последовательность {xn} называется неограниченной. Характерно, с точки зрения условий Противоположное свойство последовательности инвертируется квантификатором Существование 3 и общность V и символ «внизу») Изменено на символ «больше» на противоположной стороне (>). Одно из проявлений принципа двойственности (см. 1.4 и 1.5). Последовательность (6.3) — (6.6) ограничена, (6.5) Может быть указано число M = 3/2, а в остальном случае -M = 1 Но это возможно

Смотрите также:

Предмет математика

Равномерная непрерывность	Предел последовательности
Переменные величины	Признаки существования предела последовательности