Оглавление:







Ламинарный пограничный слой на плоской плите при переносе массы и тепла
- В предыдущем разделе мы рассмотрели массоперенос в стационарных или почти стационарных смешанных газах. Массообмен в промышленных применениях обычно более сложен, потому что существует принудительная или свободная конвекция, которая также способствует массе transfer. As масса движется от твердой поверхности к потоку жидкости, процесс движения по существу сосредоточен в пограничном слое.
Этот процесс изучается на плоской пластине, расположенной в потоке с той же скоростью, что и ламинарный пограничный слой, существующий вдоль поверхности. Чаще всего процесс теплопередачи связан с массой transfer. So например, за счет испарения с влажной поверхности или конденсации на поверхности тепло поглощается или выделяется на поверхности за счет изменения ее фазы.
Системы, у которых оболочка не препятствует обмену ни веществом, ни энергией, называются открытыми. Людмила Фирмаль
Этот процесс обычно вызывает перепад температур в жидкости, и, следовательно, передачу тепла. На практике мы часто обнаруживаем, что течение в пограничном слое является турбулентным. Но оперативной памяти Наружный поток-это модель, которая легко вычисляется и подходит для изучения основных явлений Система уравнений для пограничного слоя, описывающая момент, массу и передачу энергии вместе в двумерном стационарно-ламинарном пограничном слое двухкомпонентной смеси, имеет вид * 2.
Уравнение неразрывности а (р») _ 1_d (ПП) Р. ДХ, делай. 」 Уравнение Уравнение диффузии Уравнение переноса энергии ДТ ДТ д ДТ. / Да3 П Ср {у дю• Уравнение диффузии описывает массовое содержание компонента, удаленного с поверхности. Новый член появляется в уравнении энергии-последний член справа. Он объясняет то, о чем уже говорилось в предыдущем разделе, то есть перенос энергии связан с диффузией, даже если градиент температуры не возникает. На самом деле, диффузия также происходит, когда есть разница температур и нет градиента концентрации.
Этот процесс называется термодиффузией. Поэтому в этом случае необходимо ввести дополнительные члены в уравнение переноса массы и энергии. Однако только при очень большом градиенте температуры коэффициент температуропроводности может оказывать заметное влияние на процесс, поэтому им можно пренебречь в обычном процессе массообмена, происходящем в промышленных условиях. Это очень трудно решить приведенное выше уравнение. Их можно упростить, предположив, что характеристики жидкости постоянны Турбулентный массоперенос-это Г. Дейслер. [280].
2 для вывода этих уравнений, см. Чепмен и каулинг. В данном случае это означает, что свойства каждого компонента не только не зависят от температуры и давления, но и что свойства обоих компонентов жидкости практически не изменяются друг от друга other. In кроме того, расход может быть очень малым (менее половины единичной скорости звука), поэтому нагрев трением пренебрежимо мал. Константы также считаются скоростями вне границы layer. In в этом случае приведенная выше система уравнений упрощается и принимает вид: Уравнение неразрывности: Ди ■ ДВ ___ ЦОР * делать.
Уравнение импульса: Ди я did2i Уравнение диффузии: дециграмм. &} Уравнение энергии: (16-18) (16-19) (16-20) (16-21) Эти уравнения содержат некоторые граничные условия. Если r / = 0: u = 0; v =vₐ; w₁=wₗₐᵢ; t= t^, (16 ~22) Так. .г — + ОО: у =А$ Т =tₛ .(16-23) Массовое содержание стенки и температура tw считаются постоянными (не зависящими от x) .Условие v = vw обычно объясняет тот факт, что конвекция связана с переносом массы из surface .In в предыдущем пункте было отмечено, что если поверхность непроницаема для 1 из компонентов (испарение, конденсация), то такая конвекция всегда occurs .It также появится, когда оба компонента проходят через поверхность, если противоположный массовый расход 2 не точно такой же .
В этом случае в приведенной выше системе дифференциальных уравнений в качестве дополнительного параметра、 Конвективная скорость vₗᵥ .Позже вы узнаете, как это связано со всей передачей process .In кроме того, существует явное сходство между этими 3 уравнениями, которое помогает решить ._____ Представлены переменные, используемые в разделе 6-6, r] = (y / 2) — uₛ/ vx и f, а также следующие безразмерные параметры, описывающие массовое содержание и температуру .
Опишите дифференциальное уравнение в следующем общем виде: В результате вы получите: др) 3 ’Ди]2dudu2 d2ez .Доктор ?Я .. (пр) / ^ = 0. 3-е уравнение содержит безразмерные коэффициенты Пр = v / а. Аналогично, безразмерный коэффициент v / d появляется во 2-м уравнении при преобразовании process. It называется число Шмидта: sc = v / d Граничное условие принимает следующий вид: для y = 0:^ = 0; p ’= 0; 6 ’= 0; f =fₐ= / re = const; at#oo:^ = 1; p ’= 1; 6 ′ = 1. Граничное условие fw = const, являющееся требованием преобразования, подразумевает следующее соотношение: Постоянный/ Или vw / uₛ обратно пропорционально y / x. К счастью, это ограничение не так строго.
Это объясняется тем, что в большинстве случаев было установлено соответствие условий постоянной температуры и массовой доли фракции на поверхности. Диджей! Dy yφ ’и 6′ имеют одинаковые граничные условия. Кроме того, для sc = l и pr = ’ 1, 3 дифференциальных уравнения имеют одинаковую зависимость между этими 3 параметрами. Для такой 2-компонентной жидкости в этом случае решение следующих 3 уравнений: планка f’sp) (l) должна быть идентична Функция.
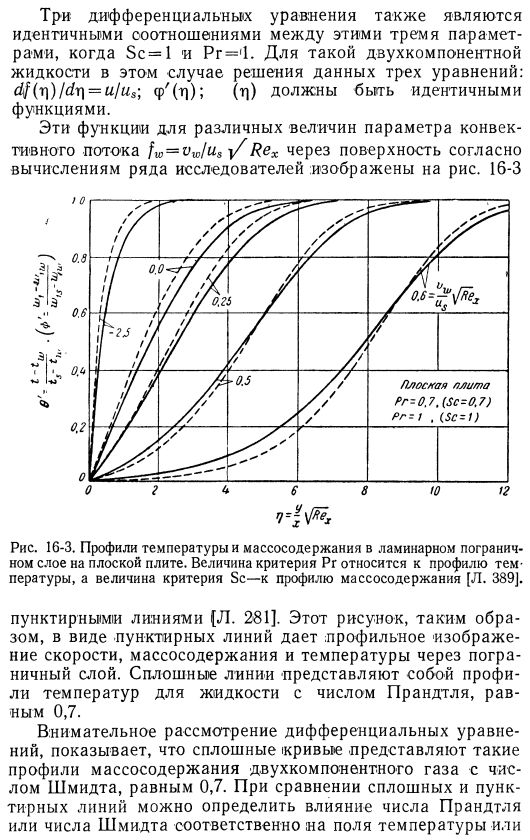
- Эти функции зависят от различных значений параметров конвективного течения re различных по поверхности Расчеты многих исследователей представлены на рисунке. 16-3. Рис. 16-3. Температурные и массовые профили ламинарных пограничных слоев на плоской пластине. Значение эталонного pr указывает на температурный профиль, значение эталонного sc — на профиль массы[l. 389j. Пунктирная Лилия (л. [281]. Таким образом, эта фигура в виде пунктирной линии дает профильное изображение скорости, массового содержания и температуры через пограничный слой.
Сплошная линия представляет собой температурный профиль жидкости с числом крапивы 0, 7. Если внимательно изучить дифференциальные уравнения, то можно увидеть, что сплошная кривая представляет собой такой профиль массы 0, 2-компонентного газа с числом Шмидта 0. 7. By сравнивая сплошную линию с пунктирной линией, можно определить влияние числа прандта или Шмидта на температурное поле соответственно Интенсивное поле.
Теплопроницаемую оболочку называют также диатермической; если такая оболочка препятствует обмену веществом, то соответствующую систему называют закрытой. Людмила Фирмаль
Очевидно, что массовое содержание и температурные профили подобны, если отношение sc / pr = a / z) называется pr = sc или число Льюиса равно 1. Такое положение часто встречается в газовых смесях, что значительно упрощает расчеты массопереноса. С инженерной точки зрения, наиболее важным является знание трения, теплопередачи и массопереноса на поверхности. Эти параметры определяются с использованием градиента поверхностной скорости, температуры 1 и массы fraction. In на рис. 16-3 видно, что остальные параметры являются постоянными. Трение, тепло и массоперенос уменьшаются конвекцией от поверхности и увеличиваются конвекцией к поверхности.
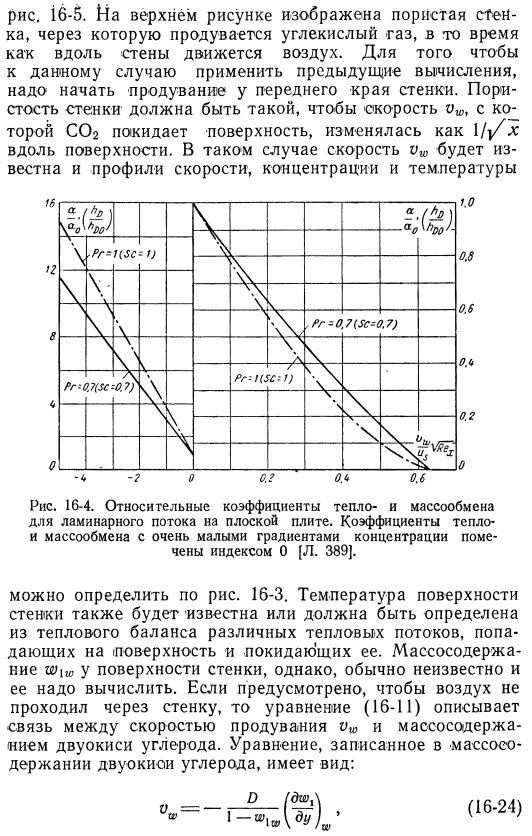
Коэффициент теплопередачи у стенки характеризуется коэффициентом теплопередачи, который определяется уравнением 1⁶-23а> Соответствующий коэффициент массопереноса может быть определен из уравнения з » ЕД. = — ДР (^) = АО (И ’|»-«’ | Л (16-236) miw представляет собой массовый расход компонента 1 на поверхности. Влияние конвекции вблизи поверхности на оба коэффициента видно на рисунке. На рис. 16-4 показана зависимость отношения фактических коэффициентов тепло-и массопереноса к очень малой (в пределах нуля) конвекции при прочих равных условиях коэффициента a xue и hdq через поверхность параметра конвекции vwluₛ^ re on.
Кривые на рисунке были построены в соответствии с соответствующим наклоном на рисунке 2, r) = 0. 16-3. Пунктирная линия относится к жидкости с pr = 1 и sc = 1. Сплошная линия представляет собой отношение-pr = 0, 7 АО в жидком случае Тогда отношение жидкости sc = 0, 7₍hdlhd₍ ₍. Ломаная линия на рис. 16-4 пропорциональна градиенту поверхностной скорости. Поэтому он также представляет собой отношение коэффициента трения ФП / ФПО. Необходимо учитывать взаимосвязь между конвекцией на поверхности и всем процессом переноса. Это соединение показано в нескольких примерах、 Рис. 16-5.
На рисунке выше показана пористая стенка из диоксида углерода. Через эту стену воздух дунут вдоль wall. To применяем предыдущий расчет в этом случае нужно начинать продувку с передней кромки стены. Пористость стенки должна быть такой, чтобы vw изменялась как 1 / p / x вдоль поверхности, скорость, с которой СО2 покидает surface. In в данном случае, скорость vw Рис. 16-4. Относительный коэффициент тепло-и массопереноса ламинарного потока на плоской пластине. Коэффициент тепло-и массообмена при очень малом градиенте концентрации определяется индексом o [l. 389]. Вы можете определить из диаграммы. 16-3.
Температуру поверхности стенки также следует знать или определять по тепловому балансу падающих различных тепловых потоков (уходящих или покидающих поверхность). Тем не менее, массовая доля ж [ж на стене, как правило, неизвестны и должны быть рассчитаны. После прохождения через стенки формула (16-11) описывает зависимость между скоростью продувки vw и массовым содержанием углекислого газа. Форма формулы, записанной в массовом содержании углекислого газа, выглядит следующим образом: (16-24).
Или, если вы создадите перестановку, введя безразмерный параметр, вы получите следующий результат: !-「 Рисунок это уравнение графически показано с использованием правого параметра, определенного из рисунка 16-6. 16-3. Используя заданный vw и известные характеристики воздушного потока, можно определить массовое содержание wᵢw поверхности пористой стенки из этого рисунка. Устройство, аналогичное показанному на рисунке figure. At 16-5, когда стены опрыскиваются пористым и холодным газом, оказалось эффективным средством, с помощью которого стены защищаются от потока горячих газов.
Уменьшить Боэдух- Х. 〜 _ __________________Эл. Fn7l] l iГl / l it l | lПl | lГ1 / / / i t l | lГi / / тт Базифиэль. Рис. 16-5. Массообмен на плите. Видимое увеличение коэффициента теплоотдачи от рисунка 16-4 означает, что температура стенок может быть значительно снижена при небольшом количестве охлаждения gas. In в литературе этот процесс охлаждения называют испарительным охлаждением. Часто в качестве охлаждения используется воздух medium. In кроме того, часть процесса-вышеупомянутый массообмен-теряет свой смысл. Рисунки 16-3 и 16-4 действительны для охлаждения испарением l На рисунке 16-5 ниже показано движение пара от поверхности воды к воздушному потоку путем испарения или испарения.
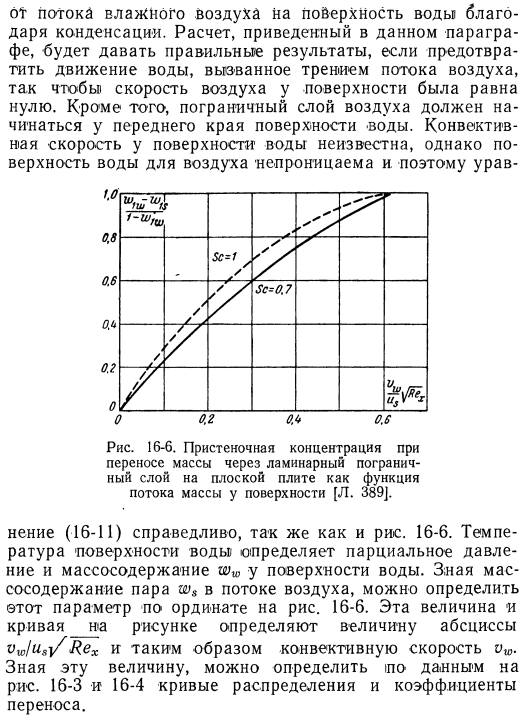
1. Воздух-для воздуха, этот процесс был рассмотрен в разделе 10-5. От потока влажного воздуха путем конденсации к поверхности воды. Расчеты, приведенные в этом разделе, дают правильный результат, когда движение воды, вызванное трением воздушного потока, предотвращается. Скорость воздуха на поверхности была zero. In кроме того, пограничный слой воздуха должен начинаться от передней кромки водной поверхности. Скорость конвекции на поверхности воды неизвестна, но поверхность воды не пропускает воздух.
Следовательно, уравнение Рис. 16-6. Париетальная концентрация при массопереносе через ламинарный пограничный слой на плоской пластине как функция поверхностного массового потока[l. 389]. Как и на рисунке (16-11), связь также верна. 16-6. Температура воды определяет парциальное давление на поверхности воды и массовое содержание ww. Зная массовое содержание пара в воздушном потоке, можно определить этот параметр по ординате рисунка. 16-6. Это значение и___диаграмме кривой определить значение абсциссы vw / u» — / re therefore поэтому конвективная скорость vw. Если вы знаете это значение, вы можете судить по данным на рисунке. Кривая распределения и коэффициент передачи 16-3 и 16-4.
Смотрите также:
| Основные уравнения и i—d диаграмма влажного воздуха | Интегральные уравнения диффузионного пограничного слоя |
| Диффузия | Подобие процессов массообмена и теплообмена |

