Оглавление:








Основные уравнения и i—d диаграмма влажного воздуха
- В расчетах, связанных с влажным воздухом, удобно брать все уравнения за счет сухого воздуха в 1 килограмм, так как содержание водяного пара изменяется. Масса водяного пара на 1 килограмм сухого воздуха называется удельной, а для содержимого она обозначается буквой d.
Из предыдущего уравнения это выглядит так: (15-1) Молекулярная масса водяного пара составляет 18 (mo = 18), молекулярная масса воздуха-29 (aga == 29). Отсюда д = 0. 622 — ^ = 0. 622 -. РА Р-Ра (15-2) При различных температурах максимальное количество водяного пара, содержащегося в воздухе, может быть различным. Воздух с максимальным содержанием водяного пара называют насыщенным.
Такие системы называются термодинамическими системами. Людмила Фирмаль
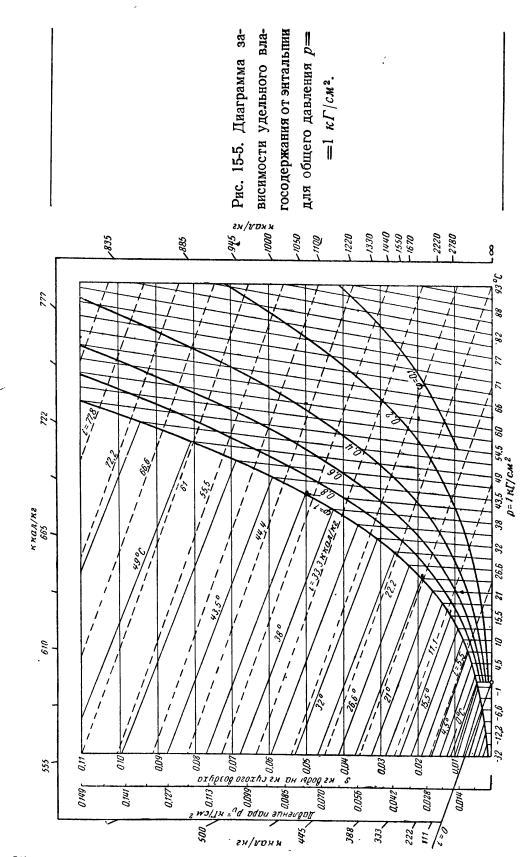
Точка насыщения определяется условием, что парциальное давление водяного пара не может превышать давления насыщения водяного пара, соответствующего температуре воздуха. Давление насыщения, которое соответствует различным температурам, можно определить из номограммы рисунка. 15-5. Удельное содержание влаги в насыщенном воздухе определяется по формуле ^ = 0. 622 -^ -, (15-3) Где p $ — давление насыщения.
Влажность часто выражается как отношение фактического парциального давления пара pᵥ к насыщенному давлению p при температуре воздуха. Такое отношение Она называется относительной влажностью и обозначается буквойp. Ф = (15-4) Иногда вместо коэффициента парциального давления принимается определенный коэффициент влажности. Отношение Ф = ’ (15-5).
Это может быть выражено парциальным давлением воды vapor. At низкие температуры, парциальное давление водяного пара меньше, чем атмосферное pressure. In в этом случае вместо формулы (15-2) можно написать: 0. 622 — П Для насыщенного воздуха Отсюда dₛ-0. 622 собой. В результате, нет никакой разницы между phi и ip при низких температурах. Избыток воды сверх прежнего влагосодержания при насыщении содержится в воздухе только в виде мелких капель (туман) или твердых в виде снега.
Содержание влаги в 1 кг воздуха составляет (d-dₛ). В последующих расчетах необходимо знать энтальпию влажного воздуха. Если удельное содержание влаги не превышает предела насыщения, то энтальпия влажного воздуха будет складываться из энтальпии сухого воздуха и энтальпии пара. Энтальпия сухого воздуха равна iₐ-cₚₐt при указании удельной теплоты воздуха при постоянном давлении через cp’.
При низких температурах она может быть выражена в виде: Здесь с-удельная теплоемкость водяного пара при постоянном давлении, удельная теплоемкость испарения при 0°С, энтальпия влажного воздуха «=», +dⁱᵥ = cₚₐt + d»), (15-6) Где б? Pa = 0, 24 ккал / кг град} c ^ = 0, 47 ккал! Кг град и i₀ = 595 ккал! Кг. Если воздух перераспределяется с водяным паром, то необходимо добавить энтальпию воды к жидкой фазе if =cftₜ, где cf-удельная теплоемкость воды (^=1 ккал!). Кг-град). Следовательно, i =cₚₐt + d (cₚᵥt + ic>₀) + (rf-dₛ) c, т. е. (15-7) Энтальпия льда/. = = — +И тепло плавкое iqq льда составляет 80 ккал} кг, а удельная теплоемкость льда составляет около 0, 5 ккал / кг град.
Энтальпия жидкофазной воды при 0°С считается равной нулю, поэтому энтальпия льда отрицательна. Туман от кристаллов льда и энтальпии воздуха ’■=+ДС+»». О) » (*»О (’о -? (15-8) ) для d ^dₛ необходимо применить формулу (15-6). Для d > dₛ и/> 0°c справедлива формула (15-8). В ненасыщенном воздухе водяной пар становится похожим на перегретое состояние. Это объясняется тем, что упругость пара меньше давления насыщения, соответствующего температуре воздуха. При особых условиях воздух может содержать больше водяного пара, чем водяной пар, соответствующий состоянию насыщения.
Это возможно, например, при резком охлаждении воздуха (при адиабатическом расширении), или при очень чистом воздухе, который не содержит твердых взвешенных частиц (пыли, сажи), из которых могут образовываться капли. Это состояние называется перенасыщением. С практической точки зрения, такое положение дел не столь важно. Поэтому предположим, что перенасыщение не происходит в следующем представлении. Процесс сушки и увлажнения обычно изучают с помощью психрометрического графика влажного воздуха. На таком графике температура (с помощью сухого термометра) строится вдоль горизонтальной оси, а удельное содержание влаги-вдоль вертикальной оси. Р.
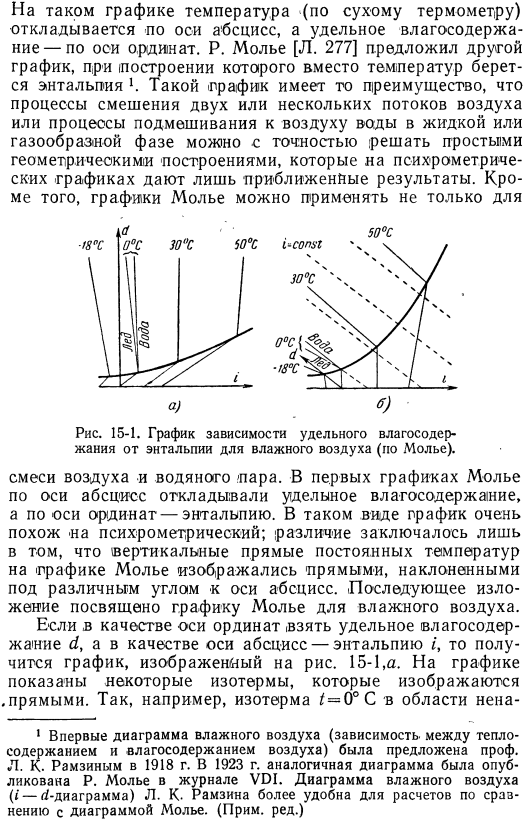
Молли. 277] предложил другой график структур, где вместо температуры используется энтальпия. Такое движение имеет то преимущество, что процесс смешивания воздуха с жидкой или газообразной водой или процесс смешивания жидкости с воздухом могут быть точно решены с помощью аэродинамической простой геометрической структуры (график показывает только приблизительные результаты). Рис. 15-1. График удельного влагосодержания энтальпии влажного воздуха (по моллюску). Смесь воздуха и воды vapor. In первый график moglier, содержание влаги было нанесено вдоль абсциссы и энтальпии вдоль ordinate. In эта форма графика очень похожа на измерение влажности.
Единственное отличие заключается в том, что вертикальная линия постоянной температуры на графике moglier была нарисована как линия, наклоненная под разными углами относительно горизонтальной оси. Следующая презентация посвящена более плотному графику увлажнения воздуха. График, показанный на рисунке, может быть получен путем взятия удельного содержания влаги dₜ в качестве вертикальной оси и энтальпии/в качестве горизонтальной оси. 15-1, a. На графике показаны некоторые изотермы, которые рисуются как direct. So, например, в области .
Изотерм/ = 0°c 1 впервые диаграмма влажного воздуха (соотношение между количеством тепла и количеством влаги в воздухе) была предложена профессором. Л. Хорошо. Рамзин В. 1918. In 1923, Р. Аналогичная диаграмма была опубликована в журнале vdi by mollieu. Л. Хорошо. Фигура влажного воздуха Рамзина (/- d-диаграмма) удобна для расчета в сравнении с фигурой Моллиера. (Примечание, редактировать) Высокое значение воздуха составляет 600 ккал для продольной оси! Он имеет наклон, соответствующий кг.
Если влажность высокая, то изотерма по формуле (15-7) отображается в виде вертикальной линии. Если воздух содержит твердофазную воду, то изотермы, превышающие предел насыщения, определяются по формуле (15-8). Поэтому он имеет отрицательный наклон 19, 5 к ординате и 79, 5 ккал! Это эквивалентно килограмму. Изотермы положительной температуры наклонены вправо. Изотерма тумана в воздухе при 0°С (d>dₛ) представлена вертикальной линией.
Изотермы отрицательной температуры «наклонены влево». Соедините все точки, соответствующие пределу насыщения, и получите кривую насыщения. Согласно уравнению (15-3), пределом насыщения является полное давление, определяемое кривой, а следовательно, так как весь график справедлив только для определенного давления. Кривая насыщения делит области, соответствующие ненасыщенным и насыщенным states. At на пересечении с изотермами/ = 0°С имеется небольшой зазор в Кривой насыщения.
Это связано с тем, что равновесное состояние воды и пара определяется при температурах выше 0°С, а равновесное состояние льда и пара определяется при температурах ниже 0°С. График показан на рисунке. 15-1а имеет тот недостаток, что площадь воздуха, насыщенного паром, относительно невелика. Этого можно избежать, применяя наклонную систему координат. Молли предложил дать такой градиент по оси d, чтобы изотермы= = 0°c в области пар-ненасыщенный воздух рисовались в виде вертикальных линий. Такой график показан на рисунке. 15-1, c. Линия 1 = const показана в виде прямой линии, наклоненной к горизонтальной оси на этом графике. 1.
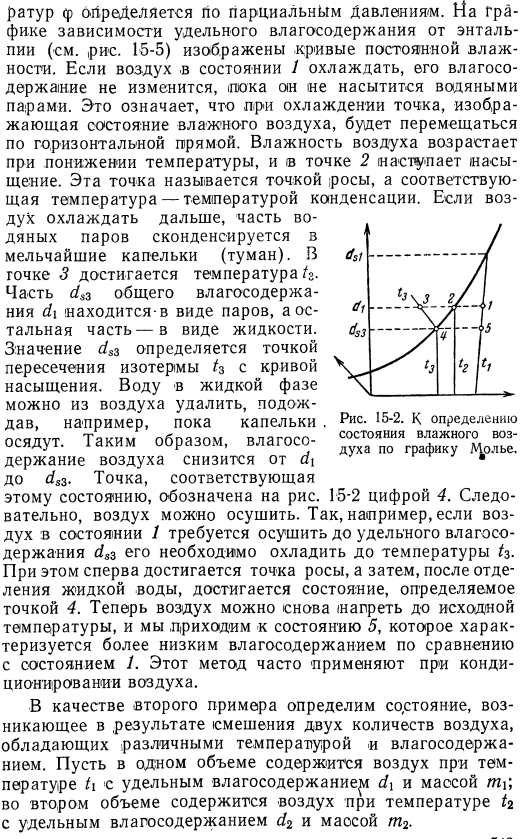
- Один из таких графиков в большем масштабе показан на рисунке. 15-5. Теперь рассмотрим несколько примеров применения такого графика. Состояние влажного воздуха при определенном давлении определяется температурой т и удельным содержанием влаги d. In рисунок 15-2, это состояние определяется точкой 1. Значение φ можно легко определить следующим образом: изотермическая Линия 1 расширяется до точки пересечения с кривой насыщения, определяет содержание насыщенной воды jₛb и определяет φ по формуле t |) i = di / rfₛi. Если температура не слишком высока, то значение влажности cp такое же.
Для высокотемпературных применений Рис. 15-2. Определите состояние влажного воздуха согласно графику. Р p определяется парциальным давлением. Зависимость удельного содержания влаги от энтальпии (см. Рис. 15-5) указывает на постоянную кривую влажности. Если воздух может охлаждаться 1, то его влажность не изменяется и он не насыщается водяным паром 1. Это означает, что во время охлаждения точки, указывающие на состояние влажного воздуха, перемещаются вдоль горизонтальной линии. Когда температура падает, влажность повышается, и точка 2 становится насыщенной.
В термодинамике изучаются физические системы, состоящие из большого числа частиц и находящиеся в состоянии термодинамического равновесия или близком к нему. Людмила Фирмаль
Эта точка называется точкой росы, а соответствующая температура называется температурой конденсации. При дальнейшем охлаждении воздуха часть водяного пара конденсируется в мелкие капельки (туман). В точке 3 достигается температура/ o. Часть общего содержания воды d dₛ₃ находится в виде пара, остальное-в виде жидкости. Значение d $₃ определяется пересечением изотермической t₃ и кривой насыщения. Жидкофазную воду можно удалить из воздуха, например, дождавшись, пока капли осядут.
Поэтому количество влаги в воздухе уменьшается от di до dₛ₃. Соответствующая точка Это состояние показано на рисунке. Номер 4 1-1. 5-2. Поэтому, воздух может быть discharged. So например, если воздух в состоянии 1 должен быть откачан до определенного содержания воды d1, то воздух должен быть охлажден до температуры t1. In в этом случае он сначала достигает точки росы, а затем, после отделения жидкой воды, достигает состояния, определенного в точке 4.
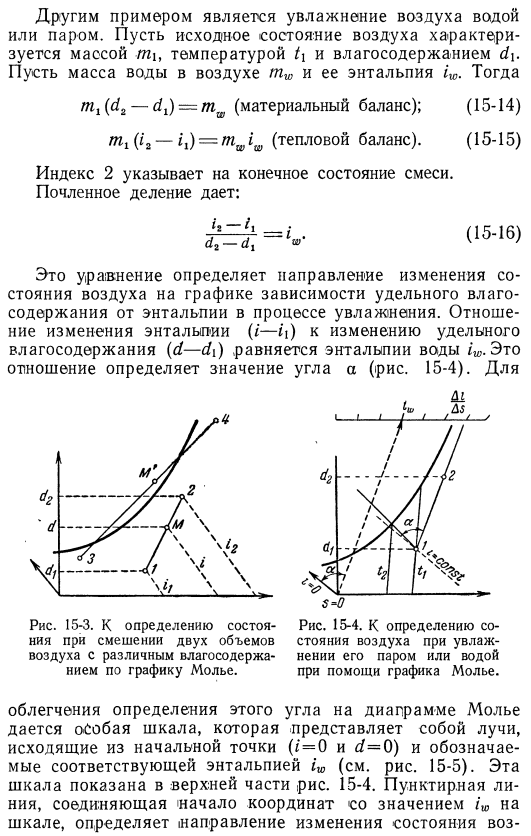
Теперь воздух можно повторно нагреть до начальной температуры, которая теперь находится в состоянии 5. Этот метод часто используется в кондиционировании воздуха. В качестве второго примера мы определяем условие, которое возникает в результате смешивания 2 объемов воздуха, которые отличаются по температуре и влажности. Позволяет воздуху с специфическим содержанием воды приспособить температуру d2 и maosm2 воздух с специфическим содержанием воды в томе d d 1 температуры mk/ 1 и 2-ом томе воздуха с специфическим содержанием влаги.
При перемешивании получают массу йоздуха массой tn при температуре t ’и определенном содержании влаги d, выполняется следующее уравнение. T₁ — — t₂= t (материальный баланс воздуха) (15-9) m₂d₂=. МД (йодный материальный баланс) ; (15-10) tnₗiₗ — — m₂i= = ttii (тепловой баланс), (15-g1) Здесь i-энтальпия влажного воздуха, значение которой можно определить из диаграммы i-d. Если вы удалите m, используя первое равенство, вы получите следующее уравнение: mₗ (д-ди-джей-ni₂ (d₂-д) ’、 — Срок отдел обеспечивает: ddₜd₂d i и ii ~~ із-я (15-12).
Из этого соотношения на графике удельного влагосодержания энтальпии точка i, характеризующая состояние смеси, должна находиться на прямой 1-2, соединяющей начальные точки (рис. 15-3). Положение точки m равно Тхи-dₜ-dt₂d-dₜ ’ (15-13) Поэтому соотношение сегмента м-2 (рис. 15-3) и сегмента М-1 должно быть равно массовому соотношению rn /м2. Когда воздух, характеризующийся состоянием 3, смешивается с воздухом, характеризующимся состоянием 4, в результате получается смесь, в которой состояние определяется точкой на прямой 3-4 (рис. 15-3).
Как видно из графика, смесь характеризуется точками, находящимися в fog. An примером этого является видимость выдоха в холодную погоду. Теплый влажный воздух, исходящий из легких, смешивается с холодным наружным воздухом, получается пересыщенная смесь, жидкая часть ее влагосодержания видна в виде тумана. Другим примером является увлажнение воздуха водой или паром. Начальное состояние воздуха характеризуется массой / mi, температурой/ 1 и влажностью d. Пусть масса воды в воздухе равна mw и ее энтальпия iw. И затем. .(d₂-dj = (материальный баланс); (t₂ — = МВт IW (тепловой баланс) .
Индекс 2 указывает на конечное состояние смеси .Срок отдел обеспечивает: Аза-id₂-d₁*> ’ (15-14) (От 15 до 15) (15-16) Эта формула определяет направление изменения состояния воздуха на графике удельного влагосодержания по энтальпии при увлажнении .Отношение изменения энтальпии (/-6) к изменению удельного содержания влаги (d-d {) равно энтальпии IW воды .Это соотношение определяет величину угла а (рис .15-4) .Для 15-3 .Согласно графику Молли, определяют состояние при смешивании 2 объемов воздуха с различным количеством влаги .15-4 .
Карты моллюсков используются для определения состояния воздуха при его увлажнении паром или водой .Для облегчения определения этого угла диаграмма Мориэля дает специальную шкалу, которая представляет собой луч, исходящий из начальной точки (/=0 и cf = O) и обозначается соответствующей энтальпией IW (см .рис .15-5) .Эта шкала показана в верхней части рисунка .15-4 .Пунктирная линия, соединяющая начало координат и значение iw на шкале (определяет направление изменения состояния Дух .
Характеризуя состояние воздуха перед увлажнением через Гочуу 1 (рис .15-4), проведите прямую линию, параллельную пунктирной линии, состояние увлажненного воздуха 2 также должно находиться на этой линии .Конечное состояние этой линии, d₂, определяется количеством смешанных водных потоков .Из Формулы (15-14) это выглядит так: = (15-17) Определите расположение точек, характеризующих конечное состояние (state .Энтальпия пара характеризуется величиной порядка 555 ккал !кг .Туманный воздух становится горячим, когда смешивается с РАХ .
Энтальпия воды будет равна ее температуре .Когда вода выливается в воздух, линия изменения состояния сильно наклонена влево .Поэтому насыщенный воздух охлаждается распылением water .It странно, что воздух охлаждается даже тогда, когда распыляется вода теплее воздуха .Это объясняется тем, что вода испаряет тепло из воздуха путем испарения .Другие примеры применения графиков приведены в обсуждении ниже .Учитывая поведение смеси других газов L, график оказался очень полезным .Задачи 15-1 .At атмосферное давление, температура 10°C насыщенный воздух смешивается с воздухом .
Удельная влажность воздуха составляет d = 0, 04 .Какой должна быть минимальная температура 2-го воздуха, чтобы исключить локальное образование тумана в процессе перемешивания ?Чтобы получить ответ, используйте диаграмму на рисунке .15-5 .15-2 .Удельную влажность d воздуха при атмосферном давлении и температуре 60°С следует уменьшить с 0, 05 до 0, 02 .Каков порядок охлаждения и нагрева процессов, которые могут достичь такого результата ?В качестве охлаждающей среды такого процесса можно использовать воду при какой максимальной температуре ?
Сколько тепла следует взять и добавить к 1 / г сухого воздуха в этой последовательности (используйте рисунок 15-5) .1 .описание создания и применения такого графа дано в виде F . Bosnjakovic, Technische Thermodinamik, vol .2, расположенный в 1937 году (с русским переводом) .л / кг от Х $ (М — ’ОСО §О/ с — Д0 .1220 .Р-1кг / КМГ J и£ОПЗ .0099 С .1 .1 / / / 7 i . 4 .11 ′ 1 .Л / з-п — /G’znjl / 1-L / Z’1JJ 1 1 1 4 ^ L I / / 7 / ^ 1 Р / Ф 1 / / Ил, 88б −2220 .−2780 .15-5 .Полное давление Р = * = 1 кг}рисунок энтальпийной зависимости удельного влагосодержания см2 .15-3 .
Воздух при атмосферном давлении при температуре 71°С, относительной влажности (Р = 0, 1, температура должна быть насыщена 30°с водяным распылением или насыщенным паром при атмосферном давлении .Какова температура насыщенного воздуха в обоих случаях и какое количество воды или пара требуется на 1 кг сухого воздуха (с использованием рисунков 15-5) .15-4 .
График удельного влагосодержания энтальпии смеси топлива и пара-воздуха поможет изучить физические процессы, протекающие в карбюраторе двигателя внутреннего сгорания .Нарисуйте такой график для смеси бензина и воздуха, используя физические характеристики, включенные в различные справочники .
Смотрите также:
| Перенос массы | Диффузия |
| Основные уравнения для смесей двух компонентов | Ламинарный пограничный слой на плоской плите при переносе массы и тепла |

