Оглавление:



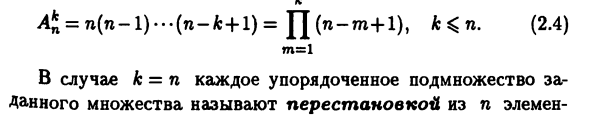





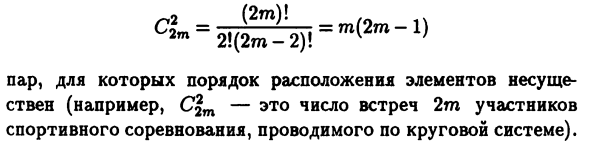


Упорядоченные множества. Элементы комбинаторики
- Определение 2.3. Установите E, отношения Этот элемент для порядка, некоторые пары ш Набор указывает, какие элементы следуют. Обозначение x y y означает, что x следует за y. отношение У заказа есть свойства: 1) х у х х 2) Для xy y и yy, xy z \ 3) Для xyy и yy xy x = y. Установить, в котором вводятся отношения порядка, Это называется частичным порядком. Под любыми двумя белыми поясами Элемент x, y, xУy множества E или Если y Y x или x = y, этот набор называется Упорядоченная. Иногда говорят: наборы упорядочены (частично Заказ) по этому заказу отношения.
Пример 2.7 а. Действительное число множества R Для x ^ y установите x y y. Указанное отношение . в Кроме того, для упорядочения любого подмножества E C R, Мы помним о естественных отношениях порядка. так Многие значения температуры на шкале термометра Упорядочены естественными отношениями порядка. б. Установите P (E) для всех подмножеств множества E Для X DY существует естественная связь порядка X Y Y. Множество P (E) частично упорядочено. с.
В зависимости от отношения заказа и свойств заказа Вещественные числа называются натуральными Людмила Фирмаль
Рассмотрим множество F действительных функций. Определен в некотором наборе Е. f, g 6 F f Y 9> если f (x) ^ g (x) Vx 6E. Набор F хотя бы частично Упорядоченная. Простейший пример упорядоченного набора: Заказанная пара (а, 6). По аналогии с ним можно поговорить Заказал тройки (а, 6, в), заказал н-ке ( 2.6). # Конечное упорядоченное множество обычно указывается Перечислите элементы и расположите их следующим образом: Введите отношение заказа и заключите его в скобки. Например, запись A = (1, 2, 3), B- (3, 2, 1) И B — различные упорядоченные наборы, Содержит те же элементы, в A отношение порядка xy y
Введено условием x ^ y, в B введено условием x ^ y. от И B, может сформировать три упорядоченных подмножества. (1, 2), (2, 3), (1, 3) и (3, 2), (2, 1), (3, 1). открытие Возможно количество различных упорядоченных подмножеств Форма выбора в соответствии с конкретными правилами элемента Некоторые наборы являются одной из задач Комбинация. Определяет набор из n элементов. Каждый он упорядоченное подмножество, содержащее k элементов, Это называется расположением n элементов по k элементам. Количество всех таких договоренностей обозначено A * в первой букве. Французское (и английское) слово расположение и значение Расположение, приборка.
- Первый элемент Вы можете выбрать размещение из n элементов в определенном наборе н улицы. Элементы размещения Повторить. Может быть использован для выбора второго элемента Только n-1 методов до A-го элемента Вы можете выбрать метод от n до +1. в В результате с помощью символа продукта П> A: A ^ = n (n-l) to- (n-k + l) = JJ (n-m + l), k ^ n (2.4) м = л каждое упорядоченное подмножество, если k = n Конкретный набор называется перестановкой из n элементов. Количество всех таких перестановок Первая буква французского (и английского) слова перестановка- Переселение. Каждая из оригинальных перестановок Набор упорядочен по родству. с того времени Перестановка элементов конечного множества Особый случай размещения элементов (когда k = n), (2.4)
Число возможных перестановок n элементов равно Тогда вместо (2.4) «T (2.6) Кроме того, предполагая условно, (2.6) становится η = k из (2.5) Как 0! = 1 каждое подмножество набора из n элементов, содержит k элементов, называемых комбинацией из n элементов К пункту. Стригущий лишай каждой комбинации Любой вид перестановки элемента (количество таких перестановок k элементов P & = &! ), Получить расположение n элементов К. Где C * — количество всех комбинаций из n элементов k (Первая буква французской комбинации или Английские словосочетания-комбинации). Отсюда Ак п * Из (2.7) Ck = C ^ ~ k и C ^ \ = C * + C * + 1. Первая комбинация этих уравнений очевидна.
Произведение всех натуральных чисел от 1 до n, n \ (произносится «эн факториал»). дорога N = п! = ф.м. (2.5) м = л Людмила Фирмаль
n элементов конечного множества, содержащего k элементов, Поддерживает комбинации, в том числе N-остальное Элементы этого набора. Второе уравнение можно интерпретировать следующим образом: Для того, чтобы исправить Часть из n + 1 элементов k + 1 комбинация элементов. Тогда, Этот элемент включен и соответствует нескольким комбинациям Остальные n и k элементов. Поэтому номер Все виды комбинаций, введенных этим элементом, равны С *. Комбинация не включая фиксацию Сформировать любую комбинацию элементов, k + 1 элементов из Остальные n предметов. Потому что это фиксированный элемент
Общее количество, включенное или не включенное в комбинацию С * + комбинация оказалась суммой всех видов комбинаций, Содержит этот элемент, но не содержит его. Настроить таблицу под названием номер C * Треугольник Паскаля, симметричный относительно вертикали, Пройдите через вершину. 1 1 1 1 2 1 13 3 1 14 6 4 1 1 С * С ** 1 1 1 K-я позиция в n-й строке таблицы — это значение C *, а крайние значения соответствуют значению C% = C £ = 1. С третьей строки внутренние элементы таблицы Равно сумме двух ближайших элементов Предыдущая строка Пример 2.8 Соответствует каждому элементу. Числовые термины {a2 a2y …, ty, …, On} (в противном случае) Биномиал) 1 + diX,% -1, n
Все значения из множества N натуральных чисел от 1 до n Включительно) и умножим их: (1 + SCX) (1 + SCX) — (1 + SCX) ••• (1 + APX) = Коэффициент 6 &, k = 1, n для любой степени k х — сумма произведений k элементов из n элементов. Указанный набор, и эта сумма включает в себя C * Срок действия. Если a1 = a2 = … = a, = … = an = 1, 6 * = C * и Это выражение называется бином Ньютона, Число C * является биномиальным коэффициентом. Используя общий символ 23 и вышеуказанное соглашение, О! (2.8) можно записать вместо 1 N / 1 я / * LP \ ^ Г * к ~ кикил \ фк = 0 Пример 2.9. Рассмотрим 2м конечное множество Элемент. Среди них согласно (2.4) и (2.7) A \ m = 2m (2m-1) упорядоченная пара Заказ парных элементов Неважно (например, C \ m — количество встреч с 2 миллионами участников Круговой турнир). найти номер я? 2т элемент методом 2м Спаривание возможно.
Любой элемент может быть в паре Форма 2т-в одну сторону. Каждый раз Формирование одной пары останется 2т. # 2t-2 способ делится на пары, то есть # 2t = (2t-1) D2t-2- Такие отношения называются рекурсией. в В этом случае # 2t можно выразить в следующем порядке. Количество способов разбить на пары 2t-2, 2t-4, … Элемент, пока не останется только два из них Только пара (L2 = 1). Вот так = (2t-1) # 2t-2 = (2t-1) (2t-3) 2t_4 = (2t-1) (2t-3) ••• # 2 = (2t-1) (2t-3) •• -3 • 1. произведение всех натуральных чисел, не превосходящих n Указывает n \, если он имеет четность, равную n (Произносится: «два факториала» или «две фабрики»). и Учитывая это обозначение, количество пар до 2t Элемент # 2t = (2t-1) !!
Смотрите также:
| Композиция отображений | Ограниченные множества |
| Произведение множеств. График отображения | Функция и ее график |

