Оглавление:

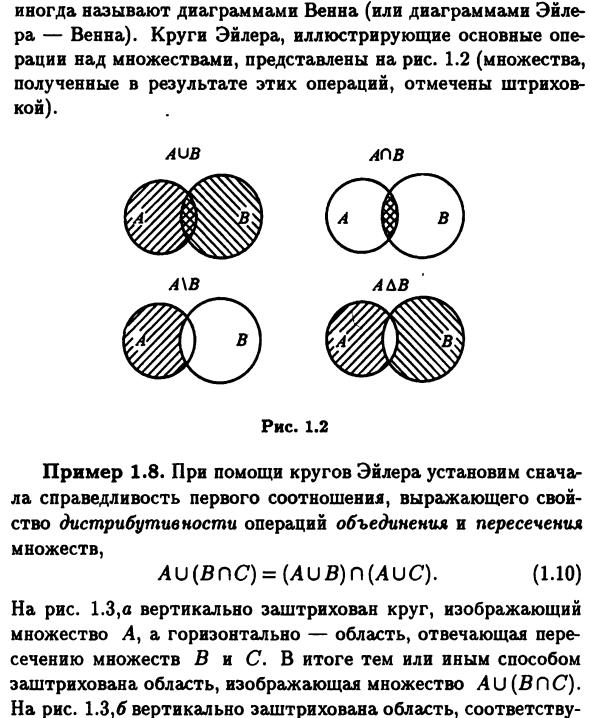


Круги Эйлера
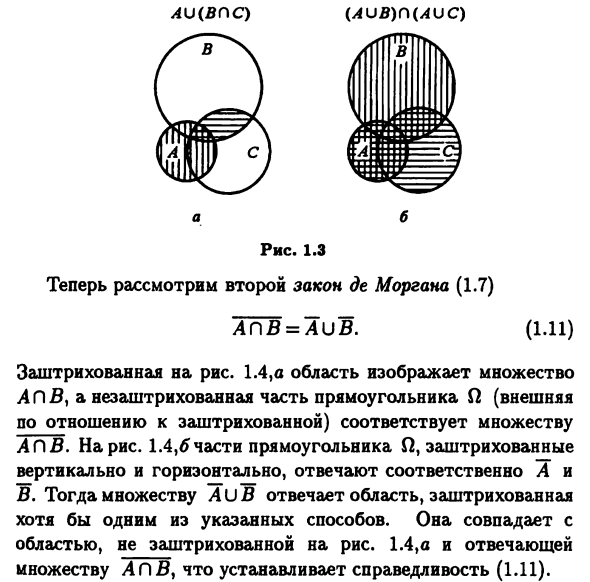
- Круги Эйлера условно называются числами Нарисуйте набор и объясните некоторые Установите свойства операции. В литературе круги Эйлера — это диаграммы Венна (или иногда их называют диаграммами) Эйлер-бен) эйлер круг показывает главное Работа набора показана на рисунке. 1,2 (установлено, Результаты этих операций отмечены люк). шар Арканзас A \ B ABB Рисунок 1.2 Пример 1.8. Набор с использованием круга Эйлера Правосудие первых отношений выражается первым Распределительная характеристика операций объединения и пересечения набор AU (BdC) = (AUB) n (AuC). (1.10) Рисунок 1.3, и круг заштрихован вертикально
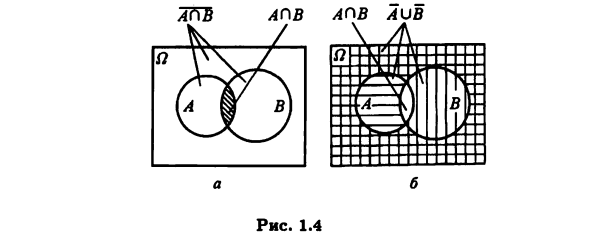
Установите в A и область, соответствующая горизонтальному направлению Пересечение множества B и C. В результате, в некотором роде Область, обозначающая установленный Au (VOS), затенена. Рисунок 1.3.6 Вертикально затененная область, Соответствует объединению множеств A и B, горизонтально Комбинировать множества A и C, оба пути Область, представляющая множество (A U B) P (A U C), заштрихована, Матч с затененной областью Рисунок метода 1.3, а. Следовательно, круг Эйлера Установить справедливость (1.10). Далее рассмотрим второй закон Деморгана (1.7) (1.11) Затененный 1.4 на рисунке, а область показывает набор £ £, и квадрат н не заштрихованная часть (снаружи (Для насиженных) AR.
Рисунок 1.4, часть квадратного фута, штриховка Вертикальный и горизонтальный, А и соответственно Б. Затем затененный набор А в затененной области По крайней мере, один из этих методов. Она Не заштрихованная область 1.4 на диаграмме и ответ Набор AP B (1.11), который устанавливает справедливость.
Смотрите также:
| Операции над множествами | Понятия отображения и функции |
| Некоторые основные логические символы | Сюръекция, инъекция и биекция |

