Оглавление:




Способ вспомогательных сфер
- Метод вспомогательного мяча 1. Существует два случая создания линии пересечения между двумя поверхностями с использованием метода вспомогательной сферы. Один из них использует сферу, взятую из одного центра, которая является общей для всех сфер в центре, а другой использует сферу, нарисованную из другого центра.
- В первом случае существует концентрический метод, а во втором — эксцентрический сферический метод. По этой причине мы сначала обсудим пересечение коаксиальных поверхностей вращения (поверхностей вращения с одной осью). Легко видеть, что две коаксиальные поверхности вращения пересекаются друг с другом окружностью, и последнее число равно числу пересечений поверхностных меридианов.
Сначала рассмотрим метод концентрических сфер. Людмила Фирмаль
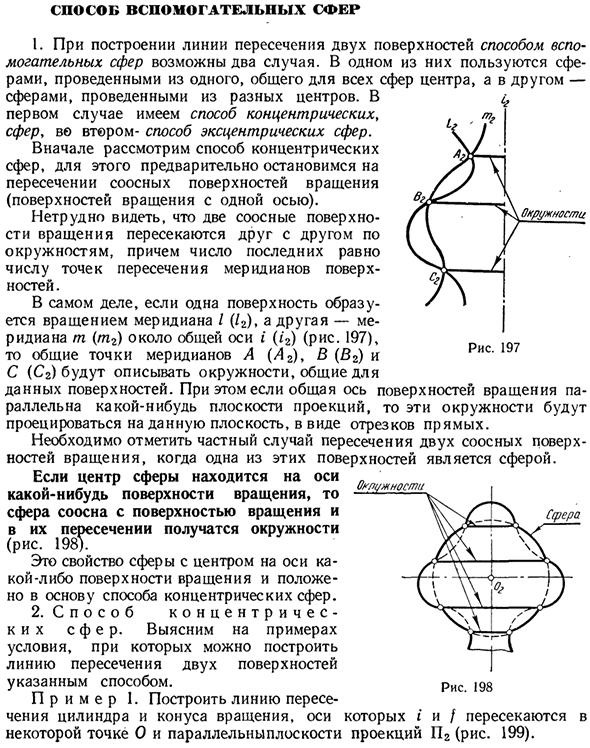
Фактически, если одна грань образована вращением меридиана / (/ 2), а другая грань является меридианом m (m2) с центром на общей оси i (i2) (рис. 197), общая точка меридиана A (A2)> B (B2) C (Cr) Поверхностные данные. Кроме того, если общая ось плоскости вращения параллельна плоскости проекции, эти круги проецируются на эту плоскость в виде прямых линий.
Если одна из этих граней является сферой, необходимо обратить внимание на особый случай, когда две коаксиальные вращающиеся грани пересекаются. Если центр сферы находится на оси плоскости вращения, сфера соосна с плоскостью вращения, и на пересечении получается окружность (рис. 198). Это свойство сферы с центром на оси вращения является основой метода концентрических сфер. 2. Концентрический шаровой путь.
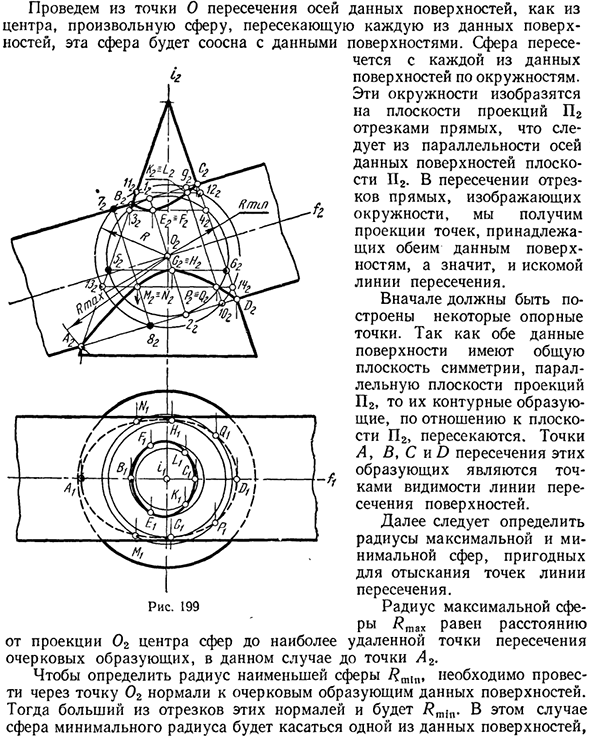
Давайте проиллюстрируем на примере условия, при которых пересечение двух поверхностей может быть построено, как показано. Пример 1. Нарисуйте линию пересечения между цилиндром и вращающимся конусом. Оси i и / пересекаются в определенной точке O и параллельны плоскости проекции P2 (рис. 199). круг Рис. 197 Рис. 198 Нарисуйте из точки O пересечения этих осей поверхности.
Любая сфера, которая пересекает каждую из этих поверхностей от центра, выровняет эту сферу с этими поверхностями. Сфера пересекается с каждой из этих четырех поверхностей по кругу. Эти круги представлены D на плоскости проекции P2. / По сегментам Удары от параллельности оси / I \ L, [\ s ^^ h эти поверхности \ sti® отрезок перекрестка Получите ПРЯМОЕ ФОВ «^ — Я рисую круг ^^^^ rftL * \ L ^ r ^ rС». \ 1 \
Обе данные прошли \ Yk \ from ‘\ nosti, следовательно \ ^ r ^ kU ^^ W- * линия пересечения. \ X ^ 3 ^ ^ mC ^^ Во-первых, \ Некоторые точки поддержки \ 2 \ точки построены. Обе данные \ _L поверхность имеет что-то общее Плоскость симметрии, параллельная плоскости проекции P2, и их контурные генераторы относительно плоскости P2 пересекаются.
Точка A на пересечении этих генераторов B, C, D является видимой точкой линии пересечения поверхности. Далее необходимо определить соответствующий максимум и ми-N ^ Ji ^ / минимальный радиус сферы Найдите точку на линии I пересечения. Рисунок максимальный радиус сферы 199 Rmtx равно расстоянию от центра проекции сферы 02 до самого дальнего пересечения генератора контуров, в данном случае это точка 2.2.
Наименьшая сфера /? Чтобы определить радиус M1n, нам нужно нарисовать нормали к генератору контура для этих поверхностей через линию 02. Максимум этих нормальных сегментов составляет Rmln. В этом случае сфера с наименьшим радиусом касается одной из этих поверхностей, И второе — пересекаются. Если меньшее из острых ребер равно / m1n, одна из этих поверхностей не будет пересекать такую сферу.
В этом примере сфера с наименьшим радиусом является сферой, которая касается цилиндрической поверхности. Эта сфера контактирует с цилиндрической поверхностью вокруг окружности 1-2 и пересекает коническую поверхность вдоль двух окружностей 3-4 и 5-6. Точки пересечения ξ, F и G% и этих окружностей являются точками искомой линии пересечения.
Чтобы создать другую точку для линии Сечение проведено несколькими концентрическими сферами с центром в точке O, радиус R этих сфер равен максимальная На фиг.199 изображена еще одна сфера радиуса R, пересекающая цилиндрические грани окружностей 7-8 и 9-10 и конические грани окружностей 11-12 и 13-14. На пересечении этих окружностей получим точки / (, L, M, N и Py Q, принадлежащие пересечению.
Чтобы создать горизонтальную проекцию точки пересечения линии, вы должны использовать круг на одной из этих поверхностей, который содержит желаемую точку. В этом примере удобнее использовать конический круг. Это потому, что эти круги не искажают на плоскости проекции. Если оси этих плоскостей вращения пересекаются, но не параллельны плоскости проекции, вы можете переместить их в положение, параллельное новой плоскости проекции, заменив плоскость проекции. Пример 2.
Нарисуйте линию пересечения сферы и любой плоскости вращения или оси Это перед центром сферы C (рис. 200). Концентрическая сфера, которая пересекает конкретную сферу с окружностью, может быть описана из любой точки пространства, кроме центра сферы C, а концентрическая сфера, которая пересекает конкретную плоскость вращения, может быть описана с помощью круга из любой точки на оси i.
Геометрическое расположение точки в пространстве может быть концентрической сферой, которая пересекается с окружностью, данной плоскостью вращения и данной сферой в качестве оси i поверхности. Таким образом, если концентрические сферы описываются из любой точки O (02) на оси вращения i, они пересекают эти плоскости с помощью круга.
- Следовательно, вспомогательная сфера с радиусом R на рисунке 200 пересекает плоскость вращения вдоль окружности / -2, и эта сфера пересекается вдоль окружности 3-4 (эти окружности являются отрезками на плоскости проекции P2 обращается у вас есть). Точки пересечения M и N указанного круга будут точкой пересечения интересов.
Примеры рассмотрены: Используя метод концентрических сфер, вы можете построить пересечение двух поверхностей с общей плоскостью симметрии, каждая из которых содержит ряд окружностей, которые могут пересекать общую концентрическую сферу на обеих поверхностях.
Для построения горизонтальной проекции точек линии пересечения можно использовать круг с вращающейся плоскостью, которая не искажается в плоскости проекции Oj. Людмила Фирмаль
В частности, метод концентрических сфер следует использовать при построении линии пересечения двух плоскостей вращения, где пересекаются оси. 3. Эксцентричный шаровой метод. Показанный метод построения пересечения двух поверхностей заключается в использовании вспомогательных сфер с разными центрами.
Чтобы уточнить условия, при которых этот метод может быть применен, рассмотрим пример, показанный на рисунке. 201. Как выясняется, в этом примере центр вспомогательной сферы можно получить в любой точке на оси плоскости вращения. Поэтому построение линии пересечения в этом случае может быть выполнено не только методом концентрических сфер, но и методом эксцентрических сфер.
На рис. 201 показана конструкция пересечения этих поверхностей методом эксцентрической сферы. Четыре сферы нарисованы с радиусами R \ R2, R3, R4 из различных центров O1, O2, O3, O * на оси вращения i. Каждая из этих сфер пересекает эти поверхности с помощью круга, и пересечение является точкой пересечения поверхностей. Давайте рассмотрим другой пример.
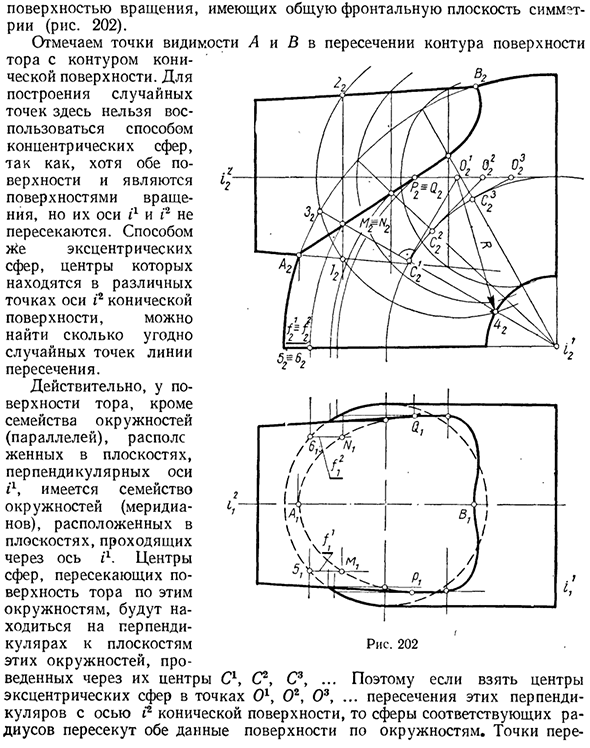
Пример. Восстановить фиговую линию 201 сечения конической поверхности тора Поворотная поверхность с общей плоскостью фронтальной симметрии (рис. 202). Отметьте видимые точки A и B на пересечении контура поверхности тора и конуса конической поверхности. Здесь вы не можете строить случайные точки, используя метод концентрических сфер.
Это связано с тем, что оси I1 и i2 не пересекаются, даже если обе поверхности являются вращающимися поверхностями. Одной и той же эксцентричной сферой с разными центрами На поверхности вы можете найти любую точку линии пересечения. Фактически на поверхности тора, кроме семейства окружностей (параллельных) в плоскости, перпендикулярной оси i1, существует семейство окружностей (меридианов) в плоскости, проходящей через ось il.
Центр сферы, которая пересекает поверхность тора вдоль этих окружностей, перпендикулярен плоскости этих окружностей, проведенных через эксцентрические сферы с центрами C1, C2, C3 и точками O1, O2 и O3. Рисунок 202 Так что, если вы берете центр. Если эти перпендикуляры пересекают ось грани конуса t2, то соответствующая сфера радиуса будет пересекать обе эти грани окружностью.
Точка Сечения окружностей на обеих поверхностях, которые принадлежат одной и той же сфере, являются точками желаемой линии пересечения. На рис. 202 три эксцентрических сферы взяты из центров 0 \ O2 и O3, с помощью которых вы находите случайные точки пересечения.
Таким образом, для построения точки M mm N рисуется меридиан из 3-4 поверхностей тора, расположенных в плоскости, спроецированной спереди через ось il (i2l) t, а перпендикуляр к этой плоскости является ее центром C1 ( С2 *). В точке O1 (02x) пересечение перпендикуляра и оси / 2 (t22) является центром вспомогательной сферы.
Теперь, если вы рисуете сферу с центром в точке O1 (так, чтобы центр радиуса R принадлежал окружности 3-4), эта сфера будет пересекать коническую поверхность вдоль окружности / -2 и окружности / -2 И обязательные точки М и N определены на пересечении 3-4 Горизонтальную проекцию пересечения можно найти, используя простые графические линии (параллельные линии) на поверхности тора.
Поэтому горизонтальные проекции M {и Ni точек M и N строятся с использованием параллельных прямых f1 и f * поверхности тора. Видимые точки P и Q конической поверхности плоскости Pi построены почти спереди. Проекции были найдены на пересечении передней проекции линии пересечения и оси t2 конуса. Примеры рассмотрены:
Вы можете использовать метод эксцентрической сферы, чтобы нарисовать линию пересечения между двумя поверхностями с общей плоскостью симметрии. Каждая из этих поверхностей должна содержать семейство кругов. При этом эксцентрическая сфера, общая для обеих поверхностей, может проходить вдоль нее.
Смотрите также:
Начертательная геометрия 1 курс

