Оглавление:





Расчет на контактную усталость активных поверхностей зубьев планетарных передач
- Расчет активной контактной усталости Зубчатая поверхность планетарной передачи Для расчета контактной усталости зубьев планетарных зубчатых колес используется та же формула для расчета простых зубчатых колес. Мощность и модуль ряда планетарных передач одинаковы (например, серия шестерен a-g-b), внутреннее зацепление сильнее внешнего, поэтому зацепление колес a и g с
одним и тем же материалом составляет только 5.1, Вариант 1). Выполняют для подбора материалов на колеса или в качестве проверки по расчету различных материалов внутреннего зацепления. В конструкции редуктора типа 3 / g расчет зубчатой передачи производится для второй ступени и полученное значение модуля берется для всех передаточных колес.
Требование равной прочности колес достигается за счет уменьшения длины зубьев колес на первом Людмила Фирмаль
этапе. При проектировании многоступенчатой передачи типа 2k-h общее передаточное отношение делится между ступенями таким образом, что оно уменьшается от ступени к ступени 25…30% к току силы. 6ю. М. Березовский и др. 1615.3 d», dt, u12, N^содержится в формуле расчета зубьев, приведенной в таблице. 5.1 Варианты трансфера Дополнительные условия РФПЛ»»»= Но В Д Е 3 / g е-G г
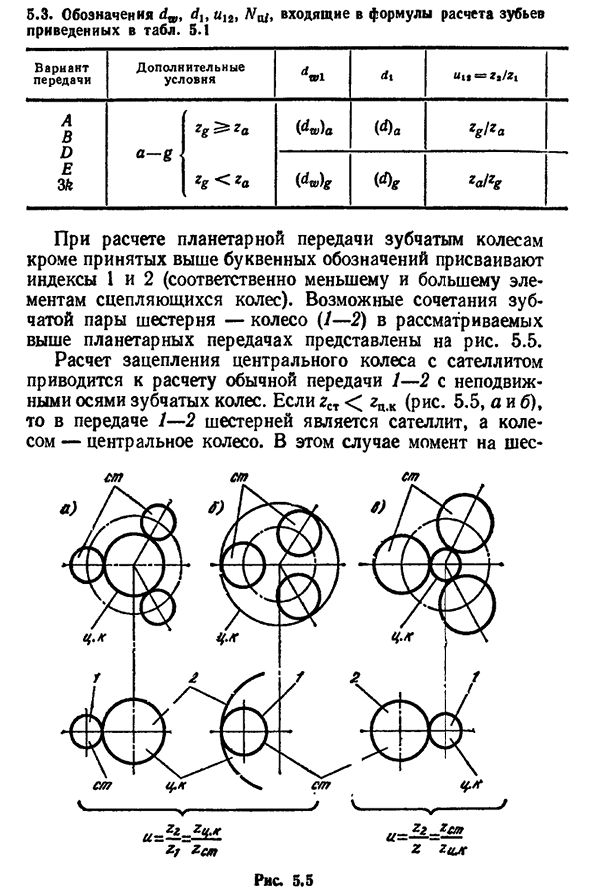
г^г(^У)а (ФА г г₽/г Ге<г (Ф? за!ЗГ Кроме названий вышеприведенных букв, присвоенных индексам 1 и 2(малый и большой элементы сцепного колеса соответственно), на рисунке показаны возможные комбинации зубчатых пар зубчатого колеса(/-2) в вышеприведенных планетарных передачах, которые вычисляют планетарные передачи. 5.5. Расчет зацепления центрального колеса со спутником приведен к расчету обычной передачи 1-2 с использованием неподвижной оси
Смотрите также:
- зубчатого колеса. Если zCTиспользуют формулу v для определения окружной скорости, связанной с системой координат (относительно водителя h)относительно оси сцепного устройства? =©•(da)) i/2 * 103=l n? (дедвейт).- /(60 * 103), Где (dw) {- диаметр первого круга I-ro колеса и ММ; nh (==(nt-nh)). Тестирование базы данных давления смены контактов определяется по известной формуле N HO=3 0 (H B)^. Циклическая выносливость при постоянных нагрузках определяется в зависимости от типа трансмиссии и колес, которые рассчитываются по формуле, приведенной в таблице. 5.3. Эквивалентная циклическая долговечность при переменных нагрузках определяется путем
умножения полученных результатов по формуле, приведенной в таблице. 5.3, по сигналу-коэффициент изменения постоянной переменной нагрузки эквивалентен [уравнению (4.15)]. При проектировании расчета контактной усталости активной поверхности зуба диаметр деления определяется по формуле Шесть.* 12_1 Двенадцать» y , 163gde Кd-вспомогательный коэффициент;Кd=78Mpa1 / 3 на стальной барабан колеса;КД=68mpa1/3 на стальной золотник колеса;* — см. Главу 4; — ширина колеса коэффициент;(ФМ)/= = ~0.75; (ФО а)<=~. fll CI±1 Двухскоростная передача (например Тип 3&) принимает (bw) g/(bw)f=0.3…0,75, что позволяет обеспечить равную прочность
колес первой и второй ступеней. Потеря мощности и эффективности. Потеря планетарной Людмила Фирмаль
шестерни главным образом составлена потери передачи подшипника и потери шевелить и распыляя масла. Эффективность планетарной передачи t1pl обычно выражается в терминах потерь в трансмиссии, которые получаются от планеты при остановке водителя. t1p l=1-2f z~FG. (5-7)где EFD-сумма потерь планетарной передачи при остановке водителя; 2F* — сумма потерь подшипника;FG-гидравлические потери. Потеря зубчатой передачи из-за скольжения профиля определяется расчетом ее надежности. Для пары зацеплений эти потери определяются по формуле f,=2,3/, (l/z,±l / z2)или приблизительно f=0,015…0.03 Потери мощности подшипника планетарной передачи могут быть значительно больше, чем в
простой передаче, потому что симметричное расположение сателлита мощности передачи сбалансировано и не нагружает Вал и опору, а гидравлические потери планетарной передачи могут быть значительно больше, чем у простой передачи при смазке путем погружения сателлита в масляную ванну. Поскольку раздельная оценка этих потерь затруднительна, на практике используется зависимость (2F+FG)=0,15…0.03 Ниже приведен краткий анализ потерь в зацеплении планетарной передачи. Рассмотрим случай в передаче (см. табл. 5.1) и др., ведущее колесо — это когда колесо B
неподвижно: Где RA-мощность IA ведущих колес планетарной передачи, RA=M A Sha) теряется P-мощность (всегда положительная), затрачиваемая на преодоление трения при зацеплении. 164 если предположить, что потерянная мощность планет и обратный механизм примерно равны, то получим p™b P?p=M a<no=MA\<ya-e A / f*; (5.8)) Аналогичным образом, мы получим (5.9 )) В формулах (5.8) и (5.9) вместо этого поставьте знак. Приведенная выше формула справедлива для любой схемы планетарной передачи с двумя
центральными колесами и водителем (2k-h). Пример 5.4. Определите КПД передачи (см. таблицу 5.1), если GA=21, zg=36, zb=93.11^=5.44. Возьмем/z=0,1, для пары колес a и g найдем^=2, 3f3(l/z a+l / zg)=2,3. 0, l^+^j=0,0 1 7 3;для пары колес g b^=2,3. 0 , | ( ^ — 1 ) — 0 . 0 0 3 9. Общая потеря i|^ = 0 ,0173 + 0,0039 = 0,02. По формуле(5.8) 0 ,0 2 ^ 0 ,9 8 4 . Возьмем(FP+f g)=A0, 03, по формуле (5.7) Chpl находим=1-(0.0 2+0.03)=0.95.

