Расчет прямозубых цилиндрических колес на усталость

Расчет прямозубых цилиндрических колес на усталость

• Расчет прямозубого цилиндрического колеса Утомлять Сила взаимодействия. Как отмечено в 4.2, нормальная сила Fn направлена вдоль линии зацепления, которая является общей нормалью к активной поверхности зуба. Сила, действующая на зацепление, обычно является полюсом зацепления P(рис. 4.26). Растворить нормальной силы на окружную FT и радиальную прот. На множестве 102 и др определяет F t^ — W M i / d i (4.19)и выражает Fr и Fn через

него:f g=F(Fn-Ff / cosam,. Такая декомпозиция удобна для расчета зубьев, валов и опор. Сила трения в зацеплении игнорируется. Распределение сил. Как отмечено в §4.3, для обеспечения непрерывной безударной работы трансмиссии должны соблюдаться условия EA>1. При этом условии следующая пара перед выходом пары зубьев из зацепления входит в зацепление, то есть в этот период зацепляются две пары зубьев (два зацепления). В зоне двухпарного зацепления сила Fn l2 действует на зубья в некоторых предположениях.

В одном наборе зон зацепления, расположенных вблизи середины зуба или вблизи стержня зацепления, зубья Людмила Фирмаль

полностью нагружены Fn (фиг.4.27) передача Зона однопарного зацепления зависит от величины коэффициента конечного перекрытия. Расчетная нагрузка. Для проектирования рассмотрим номинальную нагрузку с учетом коэффициента нагрузки. Таким образом, удельная расчетная нагрузка равна q= = i^KK*=^Lei / cosa^ ‘ (4.20) Fn H p f-нормальные и окружные силы; — коэффициент неравномерности нагрузки по ширине венца (точнее, по длине линии соприкосновения, см. рисунок. 4.28); — коэффициент динамической нагрузки; K= — расчетный коэффициент нагрузки; bw-

ширина коронки; Ke-коэффициент, teach -;. * I:изменчивость общей длины линии контакта (для прямозубого зубчатого колеса с одной парой зубчатых передач/2=bw или KV&A B.In генерал, К8 0,95, Указывает^(F t / b^K f f a, (4.21) Где Wf-удельная расчетная Окружная сила, Н / мм, а формула (4.21) (4.20) записывается в виде q-WTHKGFIA (да). (4.22) Ухабистая 103соэффективность (Kfs и kN) — из-за упругой деформации вала, корпуса, самой шестерни, износа подшипника, ошибок изготовления и сборки, связанных между собой шестерней,

• это сложное явление будет объяснено в Примере, только принимая во внимание прогиб вала. Для риса. На рис. 4.28 показано взаимное расположение зубчатых колес с деформированными осями в случае симметричных фигур(рис. 4.28, а), асимметричный (рис. 4.28, Б) и консоли (рис. 4.28, в) положение колеса относительно опоры. Вал изгибается в противоположном направлении под действием силы сцепления. При симметричном расположении опор прогиб вала не вызывает перекоса шестерни, поэтому он практически не нарушает распределение нагрузки относительно ширины венца. Это самый благоприятный случай. При несимметричном и консольном

расположении опор колеса могут регулироваться зубьями (рис.4.28, г), перекос на угол y, приводящий к нарушению правильного контакта деформация зубьев уменьшает эффект искажения и в большинстве случаев сохраняет контакт по всей длине(рис. 4.28, г). Но V / / / / / / / M В зависимости от величины деформации 104 отдельных участка зуба перераспределяется агрузка (рис. 4.28, е). Величина последнего ограничена, так как при прочих равных условиях эффект перекоса зубьев увеличивается с увеличением ширины колеса bw. В Прирабатывающихся передачах одно из колес будет иметь твердость HB350, но иметь свой материал, а при окружной скорости

и 15 м / с, неравномерной нагрузке по ширине коронки постепенно > > 15 м / с Людмила Фирмаль

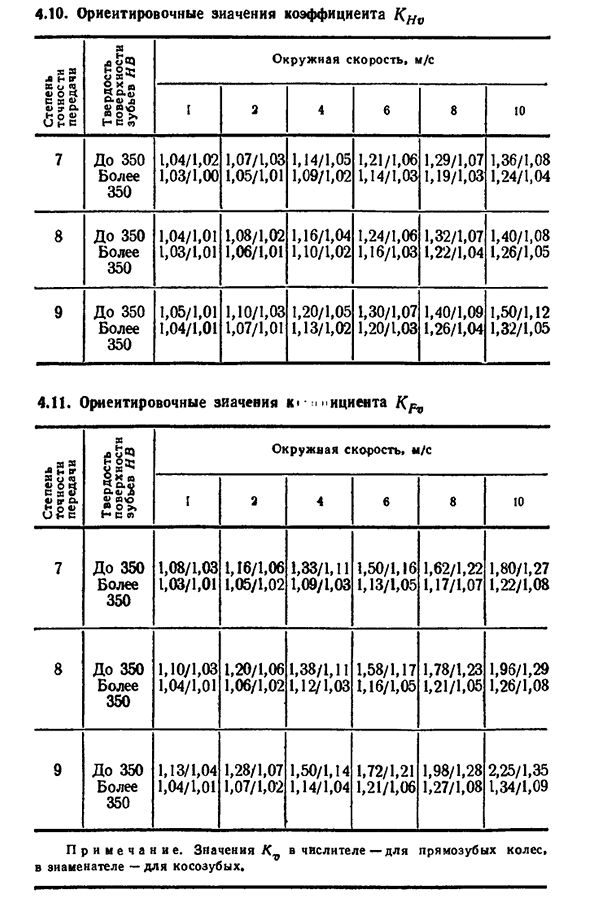
скорость, образуется устойчивый масляный слой между зубьями и защищается от истирания, поэтому работа зубьев резко ухудшается. При проектировании зубчатых колес необходимо учитывать все факторы, влияющие на неравномерность нагрузки, и в первую очередь использовать нежесткие валы, опоры и корпуса. Влияние неравномерного распределения нагрузки на ширину коронки при расчете изгибной усталости определяется коэффициентом Kf$(табл. 4.8) и при расчете контактной усталости-коэффициент КН$(табл. 4.9), который выбирается в соответствии с соотношением ширины кроны Fi. Коэффициент динамической нагрузки (Kfv и CST>) учитывает возникновение дополнительных динамических нагрузок в

зацеплении колес. Его величина зависит от скорости окружности, точности колес, веса присоединяемых деталей и других причин (таблица). 4.10; табл. 4.11). Для конических прямых шестерен значение Kv берется из графика более грубой точности, чем фактическая точность. Расчет контактной усталости цилиндрических зубчатых колес. При выводе формулы для расчета зубчатого колеса с учетом контактной усталости рассмотрим контакт зуба на полюсах с одной парой зацеплений; Приблизительное значение коэффициента K 1054.8 Размещение шестерни на опоре Твердость поверхности зуба

колеса NV od0. 4 0.6 0.8 1.2 1.6 Консольные, опорные-350 до 1,16 1,37 1,64 шарикоподшипники 350 над 1,33 1,70 Консольный, поддержка-350 до 1.10 1.22 1.38 1..57 подшипники более 350 1.20 1.44 1.71 Симметричный D o350 1.01 1.03 1.05 1.07 1.14 1.26 над 350 1.02 1.04 1.08 1.14 1.30 Асимметричный до 350 1.05 1.10 1.17 1.25 1.42 1.61 над 350 1.09. 1,18 1,30 1,43 1,73 4.9. Приблизительные коэффициенты Размещение шестерни на опоре Поверхностная твердость зуба колеса n od0. 6OD0. 4 1.2 1.6 Консольный, поддержка-350 1.08 до 1.17 1.28 шарикоподшипники 350 над 1.22 1.44 — — — Консольный, опорный-до 350 1,06 1,12 1,19 1,27 •

Подшипники ролика от 350 1,11 1,25 1,45 — — симметричный до 350 1.01 1.02 1.03. 1.04 1.07 1.11 более 350 1.01 1.02 1.04 1.07 1.16 1.26 Асимметрия Max 350 1.03 1.05 1.07 1.12 1.19 over 1.28 350 1.06 1.12 1.20 1.29 1.48 — 1064.10 приблизительные коэффициенты Степень точности передачи твердость поверхности зуба NV Окружная скорость, м / с Я Два. Четыре. Шесть. Восемь. Ага. 7 до 350 более 350 1.04 / 1.02 1.03 / 1.00 1.07 / 1.03 1.05 / 1.01 1.14 / 1.05 1.09 / 1.02 1.21 / 1.06 1.14 / 1.03 1.29 / 1.07 1.19 / 1.03 1.36 / 1.08 1.24 / 1.04 8 до 350 более 350 1.04 / 1.01 1.03 / 1.01 1.08 / 1.02 1.06 / 1.01 1.16 / 1.04 1.10 / 1.02 1.24 / 1.06 1.16 / 1.03

1.32 / 1.07 1.22 / 1.04 1.40 / 1.08 1.26 / 1.05 От 9 до 350 за 350 1.05 / 1.01 1.04 / 1.01 1.10 / 1.03 1.07 / 1.01 1.20 / 1.05 1.13 / 1.02 1.30 / 1.07 1.20 / 1.03 1.40 / 1.09 1.26 / 1.04 1.50 / 1.12 1.32 / 1.05 4.11. К<примерную стоимость белорусских l sS SW- Твердость поверхности зуба N Окружная скорость, м / с На лугу перед Я Два. Четыре. Шесть. Восемь. Ага. 7 до 350 более 350 1.08 / 1.03 1.03 / 1.01 1.16 / 1.06 1.05 / 1.02 1.33 / 1.11 1.09 / 1.03 1.50 / 1.16 1.13 / 1.05 1.62 / 1.22 1,17 / 1,07 1.80 / 1.27 1.22 / 1.08 8 до 350 более 350 1.10 / 1.03 1.04 / 1.01 1.20 / 1.06 1.06 / 1.02 1.38 / 1.11 1,12 / 1,03

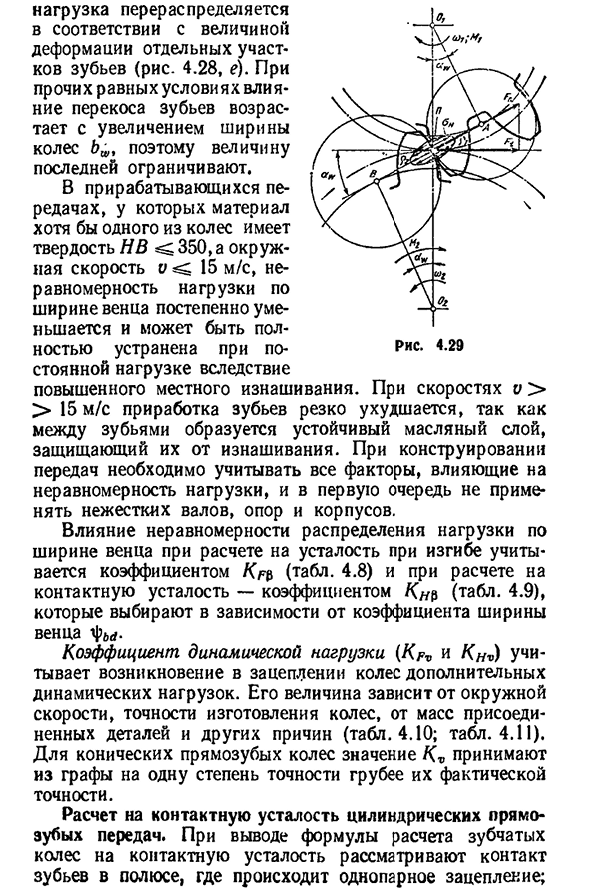
1.58 / 1.17 1.16 / 1.05 1.78 / 1.23 1,21 / 1,05 дюйма. 1.96 / 1.29 1.26 / 1.08 От 9 до 350 за 350 1.13 / 1.04 1.04 / 1.01 1.28 / 1.07 1.07 / 1.02 1.50 / 1.14 1.14 / 1.04 1.72 / 1.21 1.21 / 1.06 1.98 / 1.28 1.27 / 1.08 2.25 / 1.35 1,34 / 1,09 П р и М е ч а н и Е. числитель значений для цилиндрического колеса, в знаменателе для спирали. Сто семь. В этом случае радиус зуба считается равным двум цилиндрам, равным радиусу эвольвентного зуба. 4.29). Максимальное контактное напряжение зоны зацепления определяется по формуле Герца-Беляева. в»=в ygr2mg^г Где q-расчетное отношение нормальной нагрузки, RP p-PIPA / (Pa±) — уменьшенный радиус кривизны, EP p=2E1E2/(E1+E) — уменьшение

модуля упругости, E2-уменьшение материала шестерни и колеса. Из треугольников O1D / 7 и O2VP, сопряженного профиля Pi=(di/2) sina^,; RA=(b/g/2) запишем радиус кривизны sinajp, через них кривизну P n p-dtd2sin AWT sin aw U.* 2(d2+d1) — 2-е±T Здесь знак»плюс»,»минус» для внешнего-для внутреннего зубчатого колеса. Подставляя значения RPR и q в Формулу Герца в Формуле (4.20), заменяя sin » d, cosa^=0, 5sin2aw, получаем: 2______^НП с~^~ ~ 1 грех 2aw2l(1-Р2) Б^К^А и Zh=K2 / sin2-с учетом формы сопрягаемой поверхности зуба коэффициент (=20°zh=1,76, нормальное шпорное колесо); Z=j/ — коэффициент,

учитывающий механические свойства материала колеса. В этом случае получаем расчетную зависимость в виде, рекомендованном ГОСТом для проверочных расчетов. =]/»(4. 2-3 ) ♦Индекс коэффициента передачи I12 опущен для упрощения записи последующих выражений, 108читывая формулу(4.21), формулу (4.23), he=ZHZ»ZS [<I], Где w (- удельная расчетная Окружная сила, Н / мм, [Вт]=допустимое контактное напряжение, МПа, и Необходимо определить A™или dt при расчетном расчете установленного крутящего момента M i (M2) и передаточного отношения M12. Чтобы получить расчетную формулу для осевого расстояния AI, введите в Формулу (4.23)

следующую замену: Ft=2-103M^di=2-103M2 / diu;dt=2aw/(u±1) и bw== = ‘ Fiaoi, где FIA-осевое расстояние, то Aw для представления из этого уравнения, мы получаем. — (» ± 1) ^0—,-5—(—Z—«—Z— — A—)— ‘- K—- 3 G1OZL12K » Y в . |/. Укажите Ka=u0, 5 (ZffZ «Ze)z KH v-вспомогательный коэффициент; для прямозубых шестерен рекомендуется Ka=-49,5Mpa1’3 (при K hv=1), окончательная формула для расчетного расчета расстояния замкнутых цилиндрических прямозубых стальных шестерен aw=Ka (с±1)//, yvts2 / 0 МПа В. Для регулировки размеров указанного размера поможет числовой коэффициент 103. Если на начальном этапе проектных расчетов необходимо

определить di, то в Формулу (4.23) вводят зубчатый венец FY (/=bw/di, а коэффициент ширины по формуле Ft_2-KPAfj_2 * lQ3Af в Тогда мы получаем*7 *7 *7 1 /»2 * U1!/ * _g1 he=Z H ZuZe R’ftbli-th * ~ ]• 109 здесь разделительный диаметр шестерни (4.25 )) Где K(/=y2 (zh ZMZe) 2/^H i> — вспомогательный коэффициент, а для стальных золотниковых колес рекомендуется KD=78,0 MP1^3. Формулы (4.24) и (4.25)-H-m;-MPa;и aw-в мм;-см. таблицу. 4.9. Значения выбираются в соответствии с рекомендациями, приведенными в таблице. 4.12 Определить FY (/>fya по формуле = 2fm/(‘+1). 4.12 рекомендуется.Значение коэффициента Положение колеса относительно опоры Твердость активной

поверхности зуба НВ,<350 или НВ, а НВ,<350HB,и НВ,>350 Симметричный 0.8…1,4 0,4…Асимметричная 0.9 0.6…1,2 0,3…0.6 консоль 0.3…0.4 0.2..0.25 П р и М е ч а н и Е. наибольшее значение придается постоянной и близкой нагрузке на них за счет жесткой конструкции вала и опоры. Из приведенных ниже формул (4.23) и (4.24).Отдельно следует отметить, что величина контактного напряжения не зависит от количества модулей или зубьев, а определяется только колесами их изделий и диаметрами. Под условием усталости контакта данных di или a, модуль передачи

может произвольно малое равенство покуда mZj=di и t (?).! 4-G2)=2A. Ориентируйтесь на рекомендации, разработанные практикой, выберите значение t и проверьте усталость при изгибе. При испытании грузоподъемность большинства зубчатых колес ограничена контактной усталостью, а не усталостью при изгибе, поэтому aF может получить гораздо меньше [od]. Если расчетное значение AF превышает допустимые значения, то при допустимых значениях d и t, T увеличивается или используются колеса со смещением. Это означает, что в выбранном материале важна усталость при изгибе, а не контактная усталость. На самом деле, такие случаи происходят, когда колеса с высокой твердостью зубье

в I/?C>5 0 , При выборе 110 модулей следует учитывать следующее. Маломодульные колеса с несколькими зубьями предпочтительны для плавных условий передачи (увеличение EA) и по экономическим причинам. Однако, в случае передачи силы, порекомендованы, что принимает т2мм. Для высокоскоростной передачи, чтобы уменьшить шум, рекомендуется взять 26. Большое модульное колесо устойчиво к длительному износу и может работать длительное время после начала покраски, не чувствительно к перегрузкам и неоднородности материала (дефекты литья и др.).да что с тобой такое? Для оценки модуля следует использовать следующие рекомендации: 1. 1 нога н

а вкладке. 4.13, определить t=bw/tym, где bw=Y/KK», di получается из расчета контактной усталости. Если у нас есть Ayu из расчета, мы определяем dt-2av/(u±1), затем (и±1), bw=и затем t. 4.13 выбор модуля Особенности структуры¡t=V m’No more Высокая жесткость высокоточных шестерен, валов, опор и корпусов при высоких нагрузках: до 350 45..Тридцать. 30 на 350…Поддержка 20 обычных передач зубчатого типа с отдельным корпусом и HB с полностью жестким валом:до 350% 30..Двадцать пять 350 за 20..15 грубых шестерен (включая консольные валы) 15…Десять. П р и М е ч а н и Е

. Большое значение-для кратковременного режима работы, значительной перегрузки и средней скорости; меньшее значение 1|>т — для длительного режима работы, малой перегрузки и высокой скорости 2. Выберите модуль в соответствии с эмпирической зависимостью: t=(0,01…0,02) aw-твердость зубьев зубчатого колеса HB350; t=(0,01255…0.025) aw-когда зуб шестерни HRC>45 и твердость колеса HB350; N1t—(0.016…0,0315) aw-твердость зубьев шестерен и колес HRC 45. Полученное значение модуля округляется до значения ST СЭВ 310-76. Для стандартной коробки передач расчетное значение aw округляется до ближайшего более высокого значения в

соответствии с ST COMECON229-75: 1st2nd Количество цифр 40 50 63 80 100 125 * Сто за сорок* Сто, шестьсот. Сто восемьдесят Две сотни. Двести двадцать пять Двести пятьдесят Двести восемьдесят Триста пять 1st2nd Диапазон 355 400 Четыреста пятьдесят Пятьсот. Пятьсот шестьдесят. Шестьсот тридцать Семьсот десять Восемь сотен Девятьсот Тысяча. До 2500 etc ■При выборе Fyd рекомендуется использовать диапазон 0, J; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; г, 1.25. Расчет усталостного изгиба цилиндрических цилиндрических зубчатых колес. Расчет используется для предотвращения

усталостного разрушения зуба. Максимальное напряжение изгиба возникает при приложении вертикальной силы к верхней части зуба (рис. 4.30). Независимо от того, сколько пар зубьев задействовано, для достоверности расчетов предположим, что вся нагрузка Fn воспринимается только зубьями. Передают силу Fn по линии ее действия на ось симметричного зуба в точку С и разлагают на две составляющие:круговую F \ ‘i и радиальную F \’ r Т=ФН П О С А ‘=(М П О С а’)/п о с ‘ Р =Fn s в a’=(Ft s в a’) / c o s a w, где a ‘ — угол в направлении вертикальной силы, приложенной к вершине зуба, который немного больше угла a f.Ftlc.c&a.st я не уверен. Сила F’t сгибает зуб,а сила F’R сжимает его. Максимальное напряжение изгиба возникает на ножках зубьев зоны перехода к эвольвентному гальтелю. Существует также концентрация стресса. За расчетное напряжение в большинстве

случаев принимают напряжение на растянутой стороне зуба(BP=oiz-0CJ 112M HHt I -. Ньютон «* * * й * * 1.3 » е-ния. Для опасного участка DE вблизи струн основного круга(с учетом концентрации напряжений）) (4.26) Где W — BW S2/6-осевой момент сопротивления критического сечения ножки зуба, а a=bw S—площадь поперечного сечения ножки зуба;i-сила F’, относящаяся к критическому сечению. Значения I и S могут быть выражены модулем I-km, S=Cm зубьев, где k и C-коэффициенты, учитывающие форму зубьев. Подставляя значения, содержащиеся в выражении (4.26), вы получаете _GI cos a’_sin a’. \ О чем/? УБВ потому что да потому что ж Дж Уравнения в квадратных

скобках выражаются через YP (коэффициент профиля зуба), а уравнения для тестового расчета прямой передачи получаются путем ввода расчетных коэффициентов нагрузки KF&и kfv. (4.27) Или Чтобы получить формулу расчетного расчета, необходимо подставить в Формулу (4.27) следующее значение: Ft=2 * 103Af i / di=2•W M i / m Zi= = 2 * IfPMi/mZiir, bw = ■ di = ^решить его относительно BDM ZX tn «———- 1 0 W, K F ft F’ Покажем CT=] / r2Kfv. Значение этого кофактора согласно рекомендациям Примите КТ для шестерни шпоры гост21354-81=*=1,4. Я запишу это в конце. t=CT ‘ Около (4.28) Где t-модуль зуба, мм-крутящий момент колеса, Н-м; Zi-число зубьев шестерни: [od-

допустимое напряжение изгиба материала шестерни или колеса, МПа. Коэффициент профиля зуба Y F представляет собой безразмерную величину, которая зависит от числа зубьев g и коэффициента смещения x (таблица). 4.14). 4.14 значение Y-F внешнего зацепления при x=0 Зет >> Два. >> Два. >> 17 30 80 4 26 3,79 360 20 35 100 4,07 3,75 3,60 22 40 150 3,98 3,70 3,60 24 45 300 3,92 3,66 3 60 26 3.88 50 железнодорожных 3.65 3.63 28 65 3.81 3.62 Из-за малого количества зубьев, зубья базовых зубов тоньше, чем зубья колеса(рис. 4.31); это отражается в величине коэффициента Y F(YFl>Y FJ. Для

обеспечения приблизительно равной прочности зубьев шестерни и колеса, шестерни сделаны более сильными чем колеса. Зубья шестерни и колеса имеют одинаковую усталостную прочность при изгибе при условии[a d i / Y Fi Y F]. В формулах (4.27) и (4.28) F Y и[o/?J колеса с небольшим отношением L / y f. Значения коэффициентов Ksh>K Fv приведены в таблице. 4.8, 4.11 и 4.12. Ширина зубчатого венца bt выполняет несколько больше расчетной, учитывая возможное осевое смещение зубчатого венца из-за неточности сборки. Это условие важно при работе зубьев, когда более жесткая шестерня перекрывает ширину более мягких колес.

Смотрите также:

Предмет детали машин

Виды разрушения зубьев и критерии работоспособности зубчатых передач	Косозубые цилиндрические передачи
Выбор материалов и допустимых напряжений	Последовательность расчета цилиндрических передач