Оглавление:







Теории зацепления
- Теория взаимодействия При работе зубчатого колеса зубья одного колеса входят в полость другого колеса(рис. 4.7), зубчатая сторона ведущего колеса характеризуется прижатием зубчатой стороны ведущего колеса. Зубчатый профиль пары колес должен быть сопряженным, то есть заданный зубчатый профиль одного колеса
должен соответствовать чистому зубчатому профилю другого колеса. Чтобы обеспечить постоянство передаточного отношения, контур зуба должен быть очерчен такой кривой, которая отвечает требованиям основной теоремы зацепления. Теорема: общая Нормаль, проведенная через точки соприкосновения двух профилей, делит центральное расстояние на части, обратно
пропорциональные суммарной угловой скорости колеса. Для доказательства теоремы Людмила Фирмаль
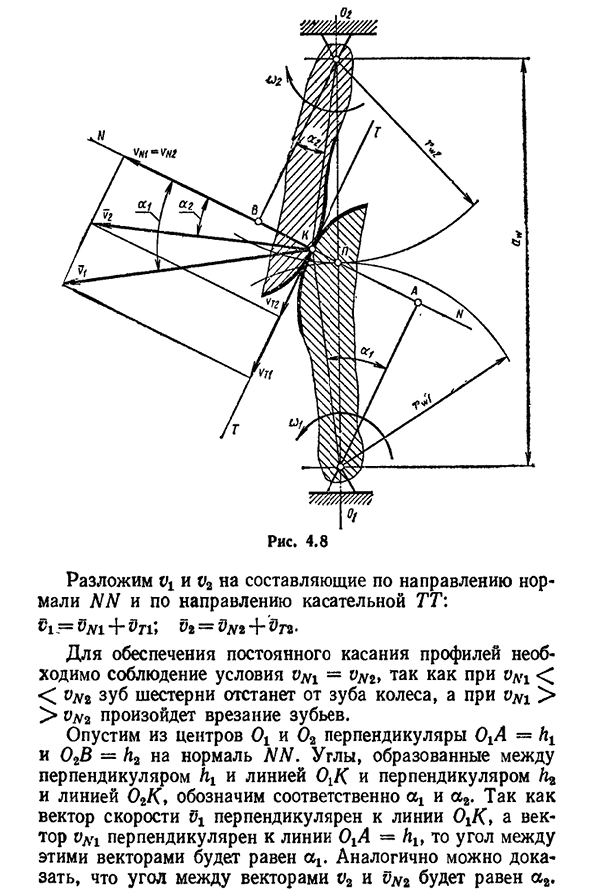
рассмотрим зацепление пары сопряженных зубьев(рис. 4.8). Профиль зубьев шестерен и колес контактирует в точке, называемой точкой зацепления. Центры вращения C\и O2 находятся на постоянном расстоянии aw друг от друга. При вращении шестерни с угловой скоростью02=5lg2+Η Η-для обеспечения постоянного профиля контакта условие vN l-vN2 является одинаковым. Опустим перпендикуляры OtA=ht и O2B-h2 от центра и O2 до нормали N. углы, образованные между вертикальными ht и линией OGK и
вертикальными h2 и линией O2K, обозначают cq и a2 соответственно. Так как вектор скорости перпендикулярен линии OHK, а вектор vN l перпендикулярен линии OtA=hlf, то угол между этими векторами также будет равен»p», вектор VN l перпендикулярен линии OtA = hlf. Три.* 67 структуры мы получаем из-за RL1=р я! = ©Я [01K] потому что Цзи — (njif, iu2=v2cos А2=(О2[МКП 02k]потому что А2-uzzz,(ОИ/второй=(O2L2 или (01 Гц Треугольное сходство из Okap и 0 2VP мы пишем его^2__r w, hi UCP~7W>’или, наконец, получаем (4.2) То, что мы хотели доказать. Для обеспечения постоянного передаточного отношения
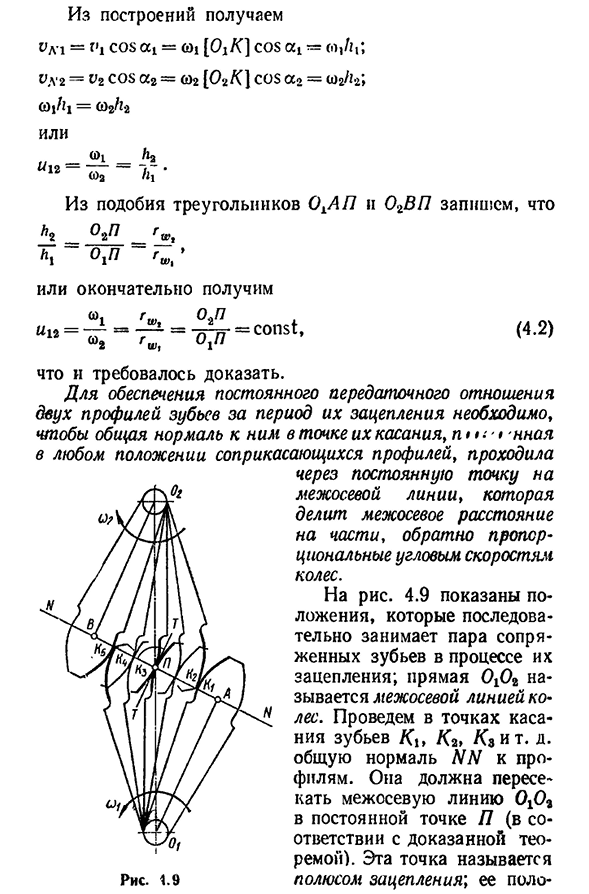
- двух профилей зубьев в течение всего времени их зацепления необходимо придать им общий нормальный, контактный профиль в момент их контакта. Рис, 1,9 GS Через определенную точку на осевой линии, разделяя расстояние центра на части, которые обратно пропорциональны угловой скорости колеса. Для риса. 4.9 обозначает положение, занимаемое последовательно парой сопряженных зубьев в процессе зацепления, прямая линия 0] 02 называется осевой линией колеса. Нарисуем точку контакта зуба Ki, K2, K3. D. общие требования к профилю. Он должен пересечь центральную линию 0 x 0 2 в фиксированной точке N (согласно доказанной теореме). Эта точка
называется «полюсом зацепления», положение на осевой линии определяется отношением угловой скорости колеса, то есть передаточным отношением. Наиболее распространенным нормальным отрезком WW, окруженным точками A и B, является траектория общей точки контакта зуба и называется линией передачи. Круг проходит через полюс зацепления и обозначается rw l и rw I. (см. Рисунок. 4.8) называется начальным кругом. Когда шестерня вращается, первый круг катит друг друга без скольжения, о чем свидетельствует окружная скорость S/o равенства! — (!2rw2 » выводится из Формулы (4.2)
. Следует отметить, что незначительное изменение межцентрового расстояния aw не изменяет положения Людмила Фирмаль
полюса зацепления, что приводит к изменению диаметра исходной окружности. Основной закон зацепления позволяет определить, какие кривые служат контуром зубьев со строго постоянным передаточным отношением. Действительно, в зацеплении все нормали к кривой, проведенной через точку контакта профиля, должны проходить через полюс зацепления. Только кривые, принадлежащие к семейству рулеток, обладают этой характеристикой. Рулетка-это другая, кривая, которая описывается точкой кривой или прямой, которая скользит по фиксированной кривой или прямой линии. В катящемся круге вы получаете
эпициклоид или гипоцикоид, когда точка рисования берется в сам круг. Прокатка круга с прямой линией дает циклоиду, а прокатка прямой линии с кругом дает эвольвенту. Самыми простыми кривыми в семействе рулеток являются циклоидные кривые (эпициклоидные и гипоциклоидные) и эвольвентные. Эти кривые используются в качестве контуров зубов. Сначала наступила циклоидная помолвка. В Циклоидальном зубчатом колесе профиль головки зуба очерчен эпициклоидом, а профиль ножки зуба-гипоциклоидом. В эвольвентных шестернях профиль зуба очерчен вдоль эвольвенты окружности вокруг оси колеса. Главным преимуществом эвольвентного зубчатого колеса является его технологичность, то есть возможность изготовления обкаткой(инструментом с прямой
режущей кромкой). Циклоидное взаимодействие в основном осуществляется путем копирования, что намного дороже. (Узнайте больше о производстве зубчатых колес 69основный круг 4.10 рис Оба метода описаны в§4.4.In кроме того, третьим преимуществом эвольвентных зубчатых колес является возможность иметь сменные зубчатые колеса, что позволяет повысить точность в узлах, где сложная передача не требует изменения осевого расстояния (радиального зазора), т. е. без нарушения законов передачи. В циклоидном зацеплении обе шестерни должны быть заменены, если необходимо изменить передаточное отношение, а в эвольвентном
зацеплении-только одна. Эвольвента круга и ее природа. Эвольвента-это кривая, описываемая произвольной точкой прямой линии, которая прокатилась без скольжения по неподвижной окружности. Например, строка N N точки A (рис. 4.10, точки от Lo до L8) объясняет эвольвенту. Длина дуги окружности, проходящей через точку соприкосновения с линией NN, всегда равна длине этой линии от точки соприкосновения с окружностью до эвольвенты (например, дуги L0B3—L3B3). Ролл видео НН радиус г окружности называется эволютой или основной окружностью, и перекрещиваем производства видео. Часть эвольвенты используется для построения профиля зуба. 4.11). Природа эвольвентной передачи зависит от природы эвольвентной передачи. 1. Эвольвента не входит внутрь
основного круга, она представляет собой спиральную кривую, которая начинается от основного круга и полностью определяется его радиусом. 2. Линия генерации NN является касательной к главной окружности и перпендикулярна всем эвольвентам, которые она генерирует. Это свойство продолжается непосредственно от сборки эвольвенты. 3. Семейство эвольвент двух или одного и того же основного круга равноудалено. Равноудаленным или равноудаленным является расстояние между двумя кривыми- Назовем это шагом P основного круга. 4. Радиус кривизны эвольвенты в любой точке равен длине касательной главной окружности, проведенной из этой точки. Центр кривизны эвольвенты в это время находится на главной окружности. Это свойство также следует
непосредственно из строительства Evol 4.11 рис Бенитес 5. По мере увеличения радиуса Эвольвента главной окружности становится более плоской и переходит в прямую линию с G6->OO. Эвольвентное взаимодействие. Рассмотрим взаимодействие двух вырожденных окружностей с центром и радиусом G1 и GM ox и O2(рис. 4.12), а вокруг него могут вращаться эвольвенты 1 и 2. В точке к’Ат я допускаю контакт эвольвент. В этой точке они имеют общую касательную и, следовательно, общую Нормаль AB. Эта Нормаль является линией генерации обоих инволютов и поэтому относится к обоим основным кругам. Из сказанного следует очень важная характеристика эвольвенты:в двух сопряженных эвольвентах радиус кривизны
касательных лежит на общей нормали. Поверните основной окружности эвольвентного 1 на некоторый угол вокруг центра Форекс от. В этом случае Эвольвента 1 оказывает давление на эвольвенту 2. Следовательно, общая Нормаль также является напорной линией. Потому что напорная линия не проходит 71, второй основной круг вместе с 0, 2, t0 эвольвентный 2, поверните на несколько углов<P2. Поэтому, возможно унести передачу движения 2 осложненными профилями. В новом положении//касательные инволюты в точке K», имеющие общую касательную и общую Нормаль относительно главной окружности, то есть обычную AB. Таким образом, общая Нормаль АВ-это геометрическое расположение точки контакта взаимодействующей эвольвенты. Из вышеизложенного линия
зацепления будет представлять собой напорную линию. Острый угол между линией зацепления и вертикалью относительно осевой линии является углом зацепления (а) для зацепления w==20°. Поскольку вращение Эвольвента не изменяет положения Oh и O2, положение полюсов не изменяется. Когда Эвольвента вращается, соответствующие дуги главной окружности ajaj и a-a2 равны общей нормали, то есть Aja’=K’K»-<VD на расстояние K’K», так что углы главной окружности ajaj и a2 равны друг другу со скоростью, пропорциональной углу поворота.,
Смотрите также:
| Расчет цилиндрических фрикционных передач | Шпоночные соединения |
| Зубчатые передачи общие сведения и кинематические характеристики | Прямозубые цилиндрические передачи |

