Оглавление:







Твердые, жидкие и газообразные тела
- Если объект, заменяющий лучистое тепло, не является полностью черным, то задача усложняется, поскольку часть лучей света отражается от поверхности. Часть лучистого тепла многократно отражается от одной поверхности к другой, пока полностью не поглощается. Влияние этого явления на теплообмен лучше всего изучать на 2 параллельных поверхностях. Расстояние между 2 поверхностями мало по сравнению с размером, поэтому почти все тепловые лучи на одной поверхности падают на other. So, угловой коэффициент для каждой поверхности равен 1.
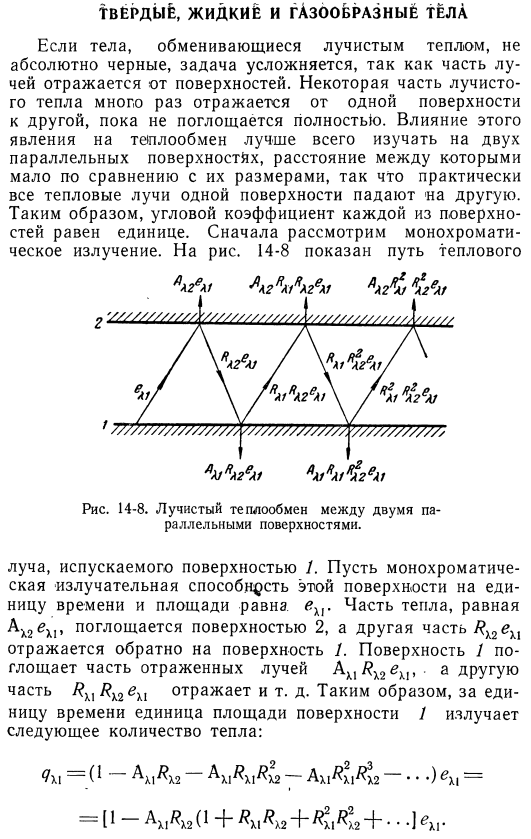
Сначала рассмотрим Монохроматическое излучение. На рисунке 14-8 показан тепловой путь 2 ’^ ////////// на. ////////////// ////////////// ^ ///// Р. ^ a2nllgea1 Д Р Р Р З Р na2l}ⁿa2eat 17777777777777777777^ 777777777777777777 ^ 7777777777777777) r2rz п АФ » a2w имеют ah1nl2ea1 aafaaf ^ 2eaf Рис. 14-8. Лучистый теплообмен между 2 параллельными поверхностями. Лучи, испускаемые с поверхности 1. Равна ex₁ монохроматической излучательной способности этой поверхности в единицу времени и на единицу площади. Часть тепла, равного ax₂ex₁, поглощается поверхностью 2, другая часть/? Икс? Ex₂ отражается обратно на поверхность/.
Считается, что первые термометры сделал Галилей в конце 16 века. Людмила Фирмаль
Поверхность 1 отражает световую линию ax₁/? X₂gx₁, поглощает часть. А другая часть ЯХЬЯХЕИ-это рефлексия и так далее. Поэтому за единицу времени единица площади поверхности 1 выделяет следующее количество тепла. = oax ω / ox₂axi /? X₁/? Xaxaxi /? ХІ ^ 2•••) ^ ХІ〜 = [1-АХА₂ (1 + ^А₂+ » + — * — kx•. Сумма терминов, заключенных в квадратные скобки, равна 1 / (1 -/? X₁ и/? Потому что x₂ меньше 1. Следовательно、 | | /? X2y.
Для непрозрачного объекта к горячему проводу справедливо равенство (13-2), а для теплового излучения-закон Кирхгофа s = a. ^x1[_ ax1 + ax2 — ’ axi ax2xⁱax1 + ax2-ax1 ax2 С другой стороны, поверхность 2 с излучательной способностью exспособ выпускает тепловые лучи на поверхность 1. Последний поглощает ax absorb, а остальные лучи отражаются на поверхности 2, поглощая часть лучистой энергии, а затем на поверхности 1. Некоторые из лучей a ₎l/? X₁/? X₂^ x2 поглощается, а остальное отражается.
Суммируя всю лучистую энергию, поглощенную поверхностью/, это выглядит так: ^ x2 Планка 0 + ^ x1 ^ x2 + ^ x1 ^ x2 ^ x2+••) ^ x2 В итоге, как и раньше, это выглядит так: _______________ ax | ax1 Ух. .2- 1-/ ?X ^ X2X2 ″ AX1 + AX2-AX | AX2X2″ Далее определим тепловой поток от поверхности 1 к поверхности 2 .?х — ^ Х1 _ AX2eX1-AX1 ^ X2 _ _ _ _ _ _ AX2eX1e6X1-AX1 eX2e6X2 AX1 + AX2 ″» AX1AX2 AX1 + AX2-AX1AX2 Это уравнение является, по сути, еще одним выводом закона Кирхгофа .Если температура двух поверхностей одинакова, то тепловой поток q должен быть равен нулю в соответствии со 2-м законом^x1 ebX2 и > термодинамики .Из приведенного выше уравнения、 Или AX1 LX2 | EX1, EX2 .
Эта формула также применима к абсолютно черной поверхности, на которой Ax и ex равны 1, поэтому результирующее соотношение всегда равно 1 .Используя формулу Кирхгофа, можно написать: (1 / — Х1) 4 — (1 / » Х2> — Я ?WI-Fi ^ ’ 1⁴ ’ 12⁾ Полная радиационная теплопередача, определяемая интеграцией по всем длинам волн, может быть выражена как: 00 .J (1/₁₁) + (1 /EX₂) — ^ » 1 ″ dl- (1⁴13) Да .Если излучательная способность представляет собой серую поверхность, не зависящую от длины волны, то формула (14-13) принимает вид: ⁼ ⁼ (1 /е。)+( ’/ «»)-! Мл .—_________——— (Г⁴_Г⁴).
Иногда, согласно формуле, мы используем коэффициенты e, _ .(14-14) Определение .(14-15) Е1, 2, Е1, Е2 .Это называется степенью уменьшения черноты системы .Тогда решение (14-14) можно описать следующим образом: 7 = e / _3 (₁₁⁴⁴- Т₂⁴) .(14-16) В других геометрических формах расчет лучистого теплообмена очень затруднен, если нет конкретных ограничений, накладываемых на излучение characteristics .In в последующих расчетах предполагается, что излучаемое излучение следует закону Ламберта Косинуса, а характеристики излучения не зависят от длины волны (серой поверхности) .
Если поверхность состоит из 2 концентрических сфер или цилиндров, излучающих диффузное излучение, то расчет, аналогичный приведенному в начале этого раздела, приведет к решению Где q-тепловой поток на единицу площади Малой поверхности Aₜ .Решение (от 14 до 17) может быть получено так быстро, как: L излучается определяет весь поток (состоящий из излучаемого и отраженного излучения) .1 .на единицу площади приходится суммарный лучистый поток в единицу времени на единицу знака, на единицу площади 2% от знака .
- Буква B была выбрана в связи с использованием такого обозначения в осветительной технике, при котором суммарный световой поток, исходящий от поверхности. Определяет brightness .In в этом случае суммарный лучистый поток с Альфа-плоскости 1 равен Л1ВЬ, а суммарный лучистый поток с поверхности 2 равен лвв2 .Только часть последнего потока, или Fâ_iaâmb₂, достигает поверхности 1 .Поскольку A_Fi_2 = A2 / ’2_|, можно легко вычислить угловой коэффициент F₂i, который surface_ /виден с поверхности 2 . / * ’j_₂= l, поверхность.
1 полностью окружена поверхностью 2, поэтому суммарный тепловой поток от поверхности а, генерируемый радиационным обменом, должен быть разностью между суммарным излучением, испускаемым этой поверхностью, и излучением, падающим на нее . е . да ^ А ^ Б-Б) .Общий лучистый поток, испускаемый с поверхности / состоит из Лучистого и отраженного излучения: = ЭИ 4- (1V₂ .Общее излучение, испускаемое поверхностью 2, состоит из излучения, испускаемого поверхностью Л₂, и отраженного излучения .=e₂4- (1 -₂) ₊ (1 — ₂₂) (1 ->>_.) .Из последних 3-х уравнений, F₂__J в= дя /A₂ дает следующую формулу: (14-18) полученные е₁=б1в₆Рe₂=e₂ebVA₁=е₁ и А₂=е₂ подставляя уравнение (14-17) — это .
Развитие научного знания о теплоте началось вместе с изобретением прибора, способного измерять температуру — термометра. Людмила Фирмаль
1 Этот метод будет использован в следующем разделе советского г .Понятно, что он был впервые использован поляком (л . 265) .Подсчет не серых поверхностей следует начинать с рассмотрения монохроматического излучения .Полная передача испепеляющего тепла в конечном счете определена интеграцией через все длины волны . 7 .дл .(14-19) Уравнение (14-12) — (14-16), как легко видеть, представляет собой теплообмен между концентрическими цилиндрами или сферами при зеркальном отражении поверхности .Это связано с тем, что лучи, испускаемые с внутренней поверхности ли, снова отражаются на этой поверхности .
Лучи, испускаемые с ₂ лица, можно разделить на 2 группы .Первая группа-это луч, который движется между A₂ и Ar, а вторая группа-это луч, который не достигает поверхности₂ .На 2 поверхностях (см .рис .14-1), которые меньше по размеру по сравнению с расстоянием от поверхности, » доля отраженного излучения, которая попадает на излучающую поверхность, снова становится незначительной .» В этом случае коэффициент ei_₂ для элементов серой поверхности будет равен е, _2 = eisr (14-20) Это уравнение представляет собой нижнюю границу приведенного значения черноты системы .
Верхний предел равен 1 .Предполагая, что поверхность стенки является серой, как и в случае радиационного обмена между двумя стенками, можно определить обмен между газом и стенкой вокруг него[L .266] .в этом случае степень уменьшения черноты газовой стенки системы eg_w равна _———————- J_, (14-21) г-Ж egooeay егоо Вот степень черноты газа (см .Рисунки 1 .3-18 и 13-19) .например, ₒₒ-это степень черноты бесконечно тонкого*слоя того же газа, которая также может быть грубо определена из рисунка .13-18 и 13-19 путем экстраполяции; — Степень черноты стен; Тепловой поток на единицу стены равен следующему ?=€о⁴⁴-eз⁴⁴ .(14-22).
Например, в пункте 1 и определяется температура газа, а в пункте 2-температура стенки .Если излучательная способность стенки велика (около 1), то коэффициент можно рассчитать с помощью: Более простые уравнения: = (14-23) Уравнения (14-21) и (14-23) точно определяют степень уменьшения черноты стенок сферического или длинного цилиндрического сосуда с газовым слоем температуры T, ограниченным между той же температурой Tw и температурой газа 3 в сосуде, 2 плоскими стенками с температурой Tw .Пример 14-1 .It необходимо определить лучистый теплообмен между стенками корабля Дьюара .
Боковые стенки, обращенные друг к другу, посеребрены .Температура жидкости в контейнере^ = 100°C, температура окружающей среды/2-20°C температура внутренней и наружной стенок сосуда приблизительно одинакова .Чернота серебра равна e = 0 .02 (при условии ep = e, см .таблицу P-10) .Степень уменьшения степени черноты системы можно определить по формуле (14-15), так как зеркальный рефлекс возникает с поверхности сосуда .I _ 1 I _ 1 e, _0 .02⁺0 .02 ″» 1 ″ 0 .01 * Тепловой поток на единицу площади внутренней стенки м = 0 .01-4 .96-10- ⁸ [ (100 + 273) *- (20 + 273) *] = 5 .95 ккал / мг .Пробковый слой толщиной для достижения такого же теплоизоляционного эффекта .
Теплопроводность трубки Х = 0, 037 ккал / л * ч * рад И затем .. 0. 037 (100-20) б — » 5. 95-0. 5 Лл Из этого видно, что изоляция сосудов Дьюара превосходна даже при учете потерь из-за теплопроводности стеклянной стенки. Если он находится между внутренней и внешней стенками, то потери тепла, вызванные излучением, могут быть дополнительно уменьшены Поместите еще одну стену серебра с обеих сторон. Когда такие стены кладутся н, с уменьшением потерь тепла определяется коэффициентом В Альфа-изоляции используется низкая лучистая теплопередача между металлическими поверхностями.
Этот утеплитель состоит из листов алюминиевой фольги на расстоянии 12, 5 мм друг от друга по всему периметру утеплителя. Тепло отводится через изоляцию излучением, теплопроводностью воздушного слоя между листом фольги и конвекцией. Если расстояние между листами фольги достаточно мало, то потери тепла за счет конвекции невелики, а потери тепла за счет теплопроводности также незначительны. Потому что воздух-отличный изолятор.

