Оглавление:


Распределения дискретных величин
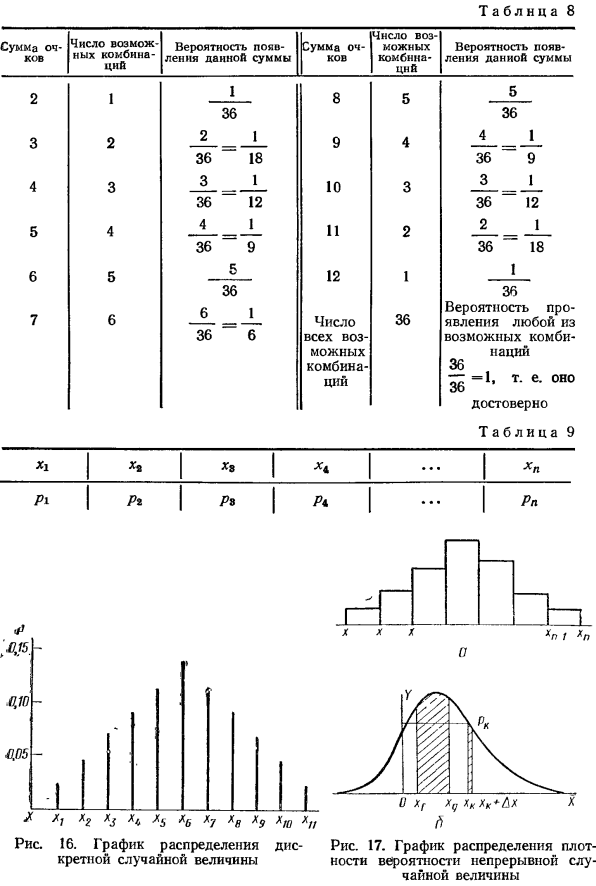
- Дискретное распределение. Чтобы полностью охарактеризовать дискретную случайную величину, необходимо и достаточно знать возможные значения и вероятность каждого из этих значений. В приведенном выше примере игры в кости число точек, выпадающих во время броска, является дискретной случайной величиной. Распределение этого значения выглядит следующим образом: Если вы бросаете два кубика одновременно, сумма очков может принимать значение от 2 до 12.
Отклонение формы и положения поверхности увеличивает ускорение движущихся частей и снижает точность парных перемещений. Людмила Фирмаль
Вероятности того, что сумма будет разной, различны. Например, всего 2 можно получить только с одной комбинацией, всего 3 с 2 (1 + 2, 2 + 1), всего 4 с 3 (1 +3, 2 + 2, 3 + 1) и т. Д. Видно из таблицы. В примере по фиг.8 количество всех возможных комбинаций равно 36. Соответствующие вероятности для каждого возможного значения суммы баллов приведены в третьем столбце таблицы. 8. В общем случае возможные значения дискретных случайных величин расположены в порядке возрастания, представленном Xi, X2, X3, X3, …, xn, и соответствующие вероятности Pb Pb Pz, pz, . Пн.
- Значение показано в таблице. 9. Такая таблица дает закон последнего распределения, если она охватывает все возможные значения дискретной случайной величины. Tab. 9 называется серией распределения и может быть представлена в виде графика. Предположим, что расстояние между соседними значениями x, то есть X3 — x и Xr — X3, …, Xn-x — xn, равно друг другу. Установите размер интервала равным 1, установите значение xs на горизонтальной оси (рисунок 16) и установите соответствующее значение для вероятности rz на вертикальной оси.
Например, при проверке измерительного трансформатора для преобразования тока или напряжения используют шунты или делители напряжения. Людмила Фирмаль
Соедините полученные точки с отрезками для ясности. Сборка лома Первый называется многоугольником распределения. Сумма всех ординат трансплантата равна 1. Суммируя ординаты графика в указанном интервале, вы можете определить вероятность того, что значение x находится в этом интервале, принимая любой интервал. В некоторых случаях распределение дискретных случайных величин может быть выражено математически. К ним относятся биномиальное распределение, распределение Пуассона и несколько других. Встроенный график рисунка 16 соответствует таблице. Восемь раздач при броске двух кубиков.
Смотрите также:
| Законы распределения случайных величин | Распределение непрерывных случайных величин |
| Дискретные и непрерывные случайные величины | Закон нормального распределения случайных величин |

