Оглавление:







Абсолютно черные тела
- Передача тепла между 2 поверхностными элементами. Если расположены разные нагретые тела с совершенно черной поверхностью, и лучи беспрепятственно проходят от одного объекта к другому, то каждый из них Тело излучает тепло к другому телу и поглощает тепло, излучаемое от другого тела. Более сильно нагретые объекты теряют больше энергии, чем поглощают. Если тело холодное, то порок versa. So. .Между горячим телом и холодным телом Рисунок 14-1 .2 поверхностная передача лучистого тепла между элементами .
Угол Лучистый теплообмен, который рассматривается в следующем утверждении: в этой главе предполагается, что поверхность радиатора полностью черная .Рисунок 14-1 dA и dA₂-поверхностные элементы 2 радиаторов .Расстояние между ними .Угол, под которым проходит линия, соединяющая Нормаль поверхности и объект формы s, равен pi и p2 соответственно .Затем, согласно формулам (13-6) и (13-7), энергия, выделяемая за единицу времени с поверхности dA в теле поверхности d2qbi, указывает на то, что поверхность dA2 равна следующим значениям: ^ 11 = r «11C⁰SM» > irfA, (H-1) .
Люди способны непосредственно ощущать холод и тепло, и интуитивное представление о температуре как степени нагретости тел возникло задолго до того, как возникли соответствующие научные понятия. Людмила Фирмаль
Где ibₙₗ-интенсивность излучения нормального элемента DAₜ, А D ^ — телесный угол, под которым элемент da * виден из элемента DAₜ .Отсюда ^ 0, = .^^ (14-2) Если подставить это выражение в выражение (14-1), то: потому что ^ потому что ^^ ^ Это тепло полностью поглощается черной поверхностью dAᵥ Аналогично найдите формулу для энергии, излучаемой от элемента dA₂ к элементуMX .d’q » = U cosp, •d ^ dA, = ibₙ₂C⁰Sp, ;, c⁰sp2dadada .(14-3) Все это тепло поглощается полностью черной поверхностью dAₜ в результате лучистой теплопередачи .Следующее количество тепла передается от элемента dAₜ к dA₂ .д’Qᵢ, =dⁱQbᵢ— д, Qb₂= (ibₙX—ibₙ₂) dAₐdAₜ .
Интенсивность излучения черного тела в направлении, перпендикулярном поверхности, определяется по формуле; ₙₗ = vrj — (*⁴ — ⁴ ) Интенсивность излучения ibₙ₂ рассчитывается по тому же уравнению .Отсюда d’qb = cos ^ cos dA, dAₐ-Ltf-T*) .(14-5) Это уравнение позволяет рассчитать радиационный теплообмен между двумя поверхностными элементами в любой ориентации .Если величина поверхности не слишком мала по сравнению с расстоянием между поверхностями, то передаваемое тепло определяется integral .
To упростив расчеты, удобно ввести новое понятие-угловой коэффициент F .угловой коэффициент dF _2 элемента dA для элемента dA — это количество тепла, выделяемого с единичной поверхности элемента da divided, деленное на излучательную способность элемента dAₓ dQb !Будет равен DAₓ { .Однако, ev₁=libₙ .Уравнение (14-1) и ( .Из (14-2), вы получите следующее: ДФ ^ = потому что П•4 = С°°П;; с, osdAₐ .(14-6) Итак, угловой коэффициент определяется чисто геометрическими соотношениями .
Здесь количество тепла, испускаемого элементом dAₓ и поглощаемого элементом dA2, может быть выражено как: d2Qb = ebidFx-2dAi- При применении уравнений (14-2) и (14-3) 、 Он описывает выражение количества тепла, которое элемент da radi излучает и элемент dAₜ поглощает .д Qb₂=1ьп2cos■ ’да > я ^ я =emfifₗ tAₜ ^ И о количестве передаваемого тепла: d2Qb= с*» .— ^2) (м — м) .(14-7) Эти вычисления также могут быть выполнены на элементе dAj, который выглядит следующим образом: = — eb₂) df_dada₂₂=* !F ^dA₂ (T} — Т) .(14-8).
Угловой коэффициент dF2 элемента dA2 для элемента dAₓ представлен следующим образом: ^, _ =±е» .Л=£= р ^ 1Б .^ Передача тепла между поверхностными элементами и окончательной пусковой площадкой .Лучистый теплообмен между 2 поверхностями можно определить по формуле (14-5) и двойному интегралу (14-7), так как размер не мал по сравнению с расстоянием между surfaces .As в результате получаем уравнение Склон cosgₜ-cosp₂ KS22 ’ l₂ Результаты интегрирования этой формулы в различные конфигурации можно найти в литературе по теплопередаче[L .262] .Внутри таблицы .
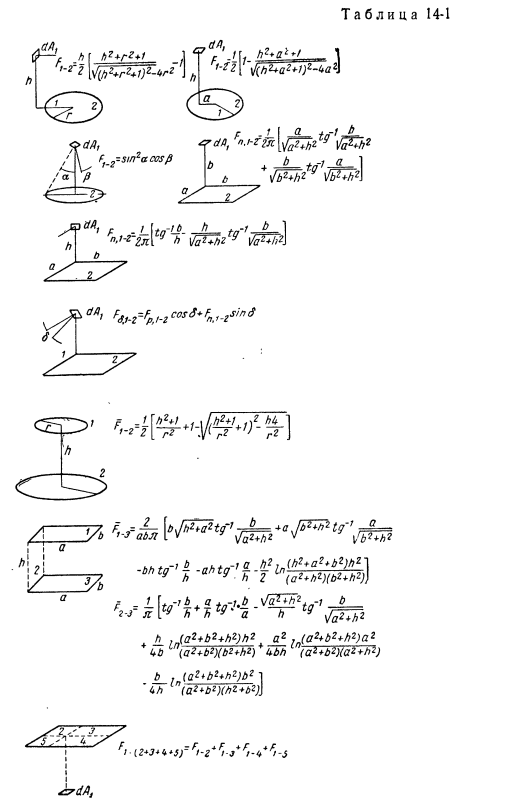
14-1-аналитическая формула для расчета углового коэффициента F .В качестве примера, используя поперечное расположение, показанное на Рис . 2, рассчитаем угловой коэффициент, характеризующий радиационный обмен между элементами области dA и Кольцевой областью A2 .14-2 .Поскольку угловой коэффициент зависит только от соотношения углов, всегда можно изменить масштаб конфигурации так, чтобы любое из соответствующих измерений имело Таблица 14-1 Л« (72*Л2 Л2 Л2+ А2;l2a2] Н (А2*В2* — В2) А2 42 ?(a2ubh (А2* БГ) (А2*В2) б (aZtb2* Н2) в21 ’4 л .T 12 * J ^ * 3) ⁼ / — г* ri J *Г1 -^ * Я .. Длина — 1.
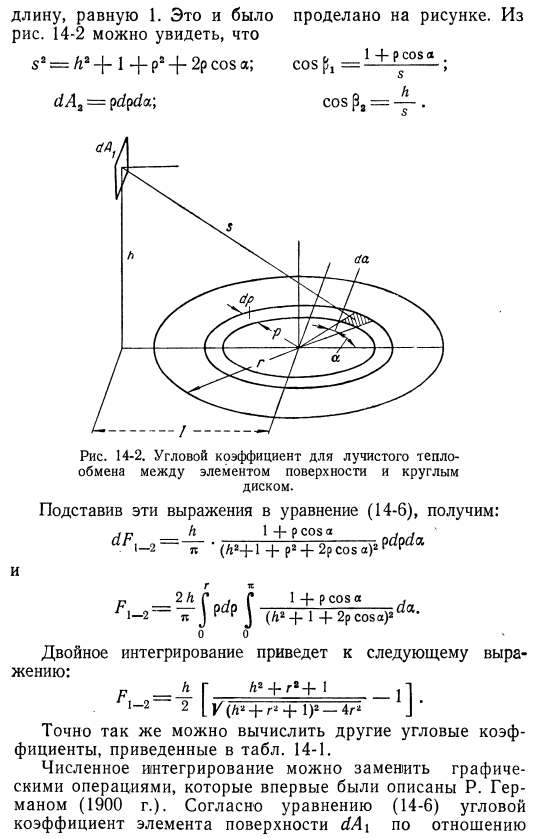
Это была та самая фигура. 14-2 вы можете видеть это С2=2П-|-1 +Р2+ 2р потому что; Это сделано на фиг. От да₃= Рис. 14-2. Угловой коэффициент лучистого теплообмена между поверхностными элементами и круговым диском. Подставляя эти выражения в Формулу (14-6), получаем: — p * (an-1 +p2+ 2pcosa) 2pc^ a И затем Г Ц ps, g 14-pcosa、 fl-2-l j rb / r j (a24-1 4-2pcosa) 2 ^ a ’ О, да. Двойное интегрирование дает следующую формулу: п р ^ + р «+ 1 1 » 221k (А24-лампа g24-я) 2-4г * й ’ Аналогично можно рассчитать и другие угловые коэффициенты, приведенные в таблице. 14-1.
- Численный Интеграл является первым r. Он может быть заменен графической операцией, описанной Германом (1900). Согласно уравнению (14-6), угловой коэффициент dai элементов поверхности равен Для площади поверхности finite конечномерной существует следующее уравнение. /? ` ₂₂ = 7 (cos (14-9) Интегрируемая формула-cos0i’rf (oi-проекция телесного угла d $ на плоскость поверхности излучения da. Интеграл-это проекция телесного угла, соответствующая сумме проекций всех фундаментальных телесных углов цаджи, или криволинейной поверхности на плоскости, где присутствует daj а отсюда можно предложить следующее composition. By центральная проекция, радиус?
В полусфере проекции разреза А₂ (рис. 14-3/отметка в). Рисунок 14-3. To определите угловой коэффициент. Опять же, создайте сечение γ таким образом, чтобы оно было ортогонально плоскости, в которой существует сечение излучающей поверхности da. Площадь 2-ой расщепленной проекции Площадь окружности i/? На рис. 2 показана величина углового коэффициента, определенного по формуле (14-9) / 1-2. Также можно использовать механический интегратор (l. 263) или оптическую проекцию[l. 264].
Аэрокосмической техники, машиностроения, клеточной биологии, биомедицинской инженерии, материаловедения и находит своё применение даже в таких областях, как экономика. Людмила Фирмаль
Для этого поместите точечный светильник в центр полусферы (рис. 14-3). Он выполнен в виде тени полусферы из молочной травы. Установите оптическую ось объектива в направлении стрелки на рис. 14-3 и установите отношение площади тени шара к площади окружности в виде: на дисплее стекла этой полусферы появится численное представление нужного углового коэффициента•на рис. 14-4 и 14-15, 2 таких рисунка. (Рис. 14-5), ОТВ К точечному источнику света в центре печи.
Фото, рисунок 14-5, сделано для определения углового коэффициента вольфрамовой нити накаливания колбы. Модель саней была размещена на небольшом расстоянии от прожектора. Рисунок 14-5. Определение углового коэффициента вольфрамовой нити накала для ламп накаливания фотографическим методом (л. 386). Рис. 14-4. Определение углового коэффициента охлаждения поверхности топки парового котла фотографическим методом[л. 386].
В результате анализа графической композиции, представленной на рисунке 14-3, могут быть получены аналитические выражения для угловых коэффициентов многих геометрических фигур без интегрирования. Это подтверждается в следующем примере. Угловой коэффициент, при котором элементы области da излучаются в прямоугольник a, может быть определен, если da параллелен прямоугольнику и меньше этого угла. Это показано на рисунке. 14-6, область а разделена линией переменного тока на 2 треугольника. Показана также геометрическая конструкция треугольника abc.
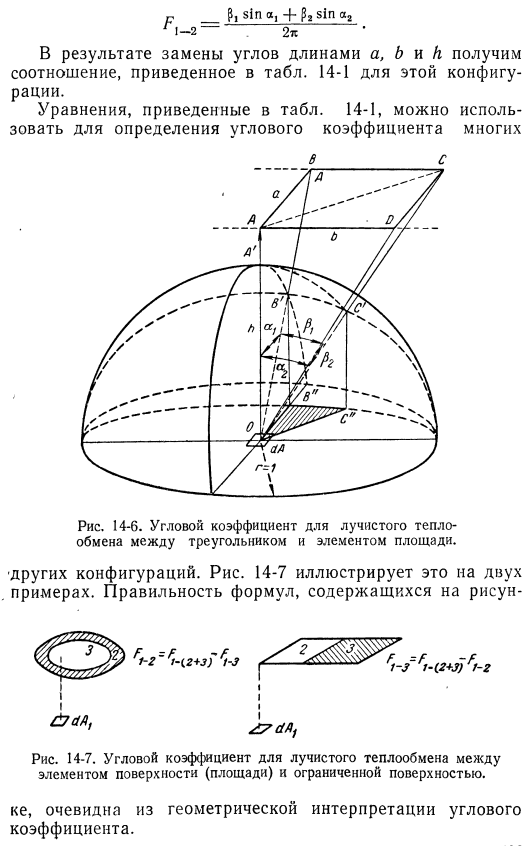
Определить угловой коэффициент фигуры ob «c» — это проекция сектора ob на большую окружность. Площадь сектора ОВ’С ’ равна значению £ 1 / 2l, умноженному на площадь окружности, или pi / 2 (радиус сферы выбирается равным 1). Таким образом, мы видим, что площадь sector «с «сектора равна (pi / 2n) sin i, а угловой коэффициент треугольника acd равен (0₂/2л) sina. Прямоугольный угловой коэффициент-это сумма угловых коэффициентов 2 треугольников, или п _ _ _ _ г, ЗША, + sina₂ Ри-2. Два ».
В результате замены углов длинами a, b и h получим пропорции, показанные на рисунке table. In эта конфигурация 14-1. Уравнение приведено на вкладке. 14-1, может использоваться для определения многих угловых коэффициентов Рис. 14-6. Угловой коэффициент лучистого теплообмена между треугольником и элементом площади. •Другая конфигурация. На рис. 14-7 показаны 2 примера. Точность уравнения на диаграмме Рис. 14-7. Угловой коэффициент лучистого теплообмена между элементами поверхности (площади) и ограничивающей поверхностью. ke, очевидно из геометрической интерпретации угловых коэффициентов.
Передача тепла между 2 торцами. Угловой коэффициент также используется для расчета радиационного обмена между ограниченной поверхностью a|. Граничная поверхность А₂ по уравнению₂? ₄ = 7, _ (^ -^). (14-10) Угловой коэффициент может быть определен из уравнения Аиаи Где f} __2-угловой коэффициент элемента daₜ в области lk. Таким образом, f_ is-среднее значение всех локальных угловых коэффициентов, облучающих поверхность la в любом месте поверхности l1.
Выражение (14-10) также может быть записано в следующем виде: (1⁴-я) Куда? А а а ^ ИИ — Средний угловой коэффициент площади Л₂ для площади л. Эти 2 угловых коэффициента связаны следующим уравнением: Эта формула полезна. Это потому, что один наклон может быть легче вычислить, чем другой. Например, если поверхность Л1 полностью окружен поверхности Л₂, все лучи, испускаемые с поверхности Л1 будет подвержена л, поэтому можно сказать Г1_₂= 1 сразу.
Внутри таблицы. На рис. 14-1 приведены аналитические выражения для нескольких угловых коэффициентов. Чтобы графически определить угловые коэффициенты ограниченной поверхности ai и ограниченной поверхности Лповерхности, поверхность a следует разделить на небольшие участки одинакового размера и структуры, показанные на рисунке. 14-3, сердце каждой из этих областей. Среднее значение всех угловых коэффициентов, определенных таким образом, равно f|.

