Оглавление:



Примеры комплексного потенциала
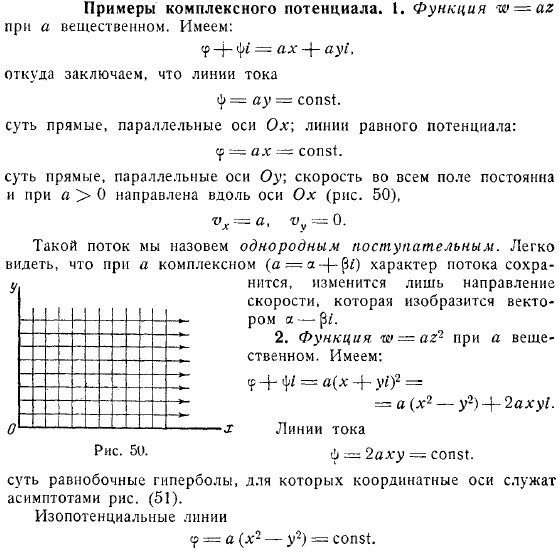
Функция гидромеханики является вещественным числом. Заключим, что линия потока является прямой линией, параллельной оси. Линия эквипотенциала. Они представляют собой прямые линии, параллельные оси. Скорость всего поля постоянна, если, то оно ориентировано вдоль оси.
Для комплекса характер течения сохраняется связь плоской гидродинамической задачи с теорией функций комплексного переменного, изменяется только направление скорости, а вектор. Текущая линия является равносторонней гиперболической, координатные оси которой функционируют как асимптота на, а эквипотенциальные линии являются гиперболическими, координатные оси которых функционируют как ось симметрии.
Очевидно, что одну из линий течения можно принять за возможную твердую границу жидкости источника и стока, а так как координатные оси служат линиями течения, то установившееся невихревое движение в пределах прямого угла является кинематическим. Функция выглядит так. Текущая строка представляет собой систему окружностей для или касательная к оси Ox в начале координат, эквипотенциальная.
Комплексный потенциал — функция двух переменных, использующаяся в гидродинамике для описания плоского стационарного безвихревого движения несжимаемой жидкости. Людмила Фирмаль
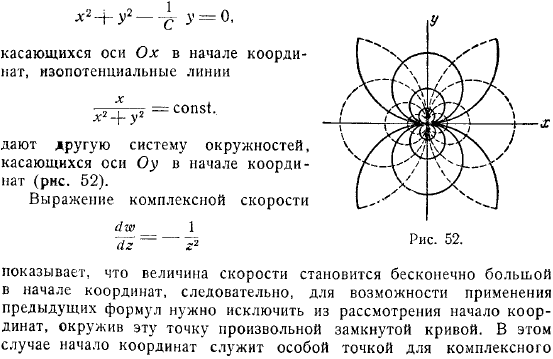
Начало координат указывает другую систему окружностей, касательных к оси. Комплексное представление скорости указывает на бесконечно большую скорость в начале координат. Поэтому, чтобы применить предыдущую формулу, необходимо исключить начало координат из рассмотрения, заключив эту точку в произвольную замкнутую.
В этом случае начало координат представляет собой особую точку комплексного потенциала (простой полюс) и комплексной скорости (двойной полюс). Функция. Комплексная переменная введение модуля и аргумента. Таким образом, обтекаемая линия представляет собой прямую линию.
Сделайте вывод, что от начала координат расходится радиально. Эквипотенциальная кривая представляет собой концентрическую плоскую окружность, центрированную в начале координат. Уравнение для комплексной скорости показывает, что в этом случае начало координат также является простым полюсом логарифма комплексного потенциала и комплексной скорости.
Действительная часть называется потенциальной функцией, мнимая часть называется функцией тока. Людмила Фирмаль

