Определение критической силы. Задача Эйлера

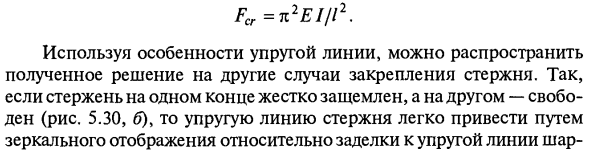
Определение критической силы. Задача Эйлера

• Определение критической прочности. Работа Эйлера Задача определения критической силы Fcr была впервые решена Л. Эйлером в 1744 году. Сила сжатия важна. Чтобы проверить изгиб, используйте дифференциальное уравнение (5.44) оси изгиба стержня. d2y / dx2 = МДж (El). (5,53) Рисунок 5.30 Изгиб происходит в плоскости с наименьшей жесткостью. Сечение вращается вокруг своей оси с минимальным моментом инерции /.

Изгибающий момент MI при абсолютном значении всех сечений равен fcr Y *, где Y ~~ — отклонение сечения. Отклонение y и его вторая производная d2 y / dx2 имеют вид Если есть противоположный знак, уравнение (5.53) выражается как: d2y / dx2 = −Fcr y / (E1). (5,54) Ввод обозначений k2 = Fcr / (EI) y (5,55) Выражение (5.54) выражается в формате y + k2y = 0. Это линейное дифференциальное уравнение второго порядка. y = Csmkx + Dcoskx. (5,56)

Чтобы определить константы интегрирования C и D, мы используем известные граничные условия, то есть условия монтажа на конце стержня: x = 0 и x = / нет прогиба, т.е. y = 0. Людмила Фирмаль

Подставляя в уравнение (5.56) >> = 0 (при x = 0), мы видим, что D-0, а стержень изгибается вдоль синусоиды y = Сsinbс. Для второго граничного условия (y = 0, если x = 1), C sin kl = 0. Если C = Oli sin kl = 0, результирующая связь действительна. Это не согласуется с исходным предположением, потому что не все поперечные сечения по длине стержня х существуют. Выражение sin kl = 0 действительно, когда /: / = ll. Где n — любое целое число (n = 0, 1, 2, …). Подставляя значение k = kn / 1 в уравнение (5.55), оно становится следующим. Fcr = k2EI = n2n2 EI / l2. Чтобы сохранить изогнутую форму стержня, сила отлична от нуля, то есть pf0. С практической точки зрения минимальная критическая сила представляет собой минимум под действием кривизны оси стержня, потери устойчивости. Если n = 1, получите минимальную критическую силу.

Fcr = k2E I / l2. Используя функцию эластичной проволоки, полученное решение может быть распространено на другие случаи крепления стержня. Таким образом, если стержень на одном конце защемлен, а другой конец пуст (рис. 5.30, б), эластичная линия стержня просто вызывается зеркальным отображением уплотнения относительно эластичной линии шарика.

• Неподвижный стержень Нирно (рис. 5.30, а). Очевидно, что критическая сила стержня с такой длиной фиксации l равна критической силе шарнирно закрепленного стержня длины 21. Общее представление о критической силе общего вида стержня сжатия принимает следующий вид с учетом его типа фиксации. Fcr = n1El / (vl) 2 (5,57) Здесь v — коэффициент уменьшения длины стержня (коэффициент Яшинского), то есть числовое значение, указывающее, сколько раз необходимо изменить длину стержня, повернутого с обоих концов (рис. 5.31, б).

Его критическая прочность равна критической прочности стержня при определенных фиксированных условиях. В большинстве случаев конец сжимаемого стержня фиксируется одним из четырех способов, показанных на рисунке. 5,31. Коэффициент уменьшения длины показан в фиксированной схеме. Застежка, показанная на рисунке 5.31, наиболее чувствительна к изгибу, а застежка, показанная на рисунке 5.31, наименее чувствительная. 5.31, д. Отметим, что использование уравнения (5.57) справедливо только в том случае, если деформация стержня сжатия в момент потери исходного равновесия является упругой. F F F V * 0,7 V * 2 против / 7P7ShTP г TP7GSh ////////// a tgsht Рисунок 5.31 б

Смотрите также:

Решение задач по прикладной механике

Контактные напряжения	Понятие об усталости материалов
Устойчивость равновесия сжатого стержня	Влияние коэффициента асимметрии цикла на усталостную прочность. Диаграмма предельных циклов напряжений

Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.