Изгиб с кручением стержней круглого поперечного сечения

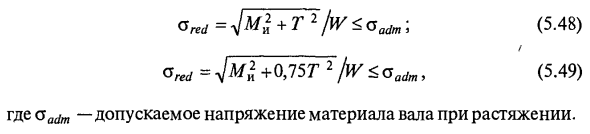
Изгиб с кручением стержней круглого поперечного сечения

• Крутильный изгиб стержня круглого сечения Когда поперечное сечение стержня деформируется сложным образом, несколько компонентов внутренней силы, таких как крутящий момент и изгибающий момент, поперечная сила и продольная сила, действуют одновременно. Расчет прочности в этом случае основан на принципе независимого действия силы с использованием выбранной теории прочности. Выбор гипотезы прочности зависит главным образом от материального состояния (пластичного или хрупкого).

Чтобы определить местоположение опасного участка, вам необходимо создать диаграмму внутренних сил. Затем определяются нормальные и касательные напряжения от каждого компонента внутренней силы. Анализируя распределение напряжений по длине стержня, определяют наиболее нагруженный участок и наиболее нагруженную точку. Для нее условие прочности создается с использованием выбранной гипотезы.

Решите эти проблемы в следующем порядке: Сначала определите внутреннюю силу на поперечном сечении стержня, используя метод поперечного сечения. Людмила Фирмаль

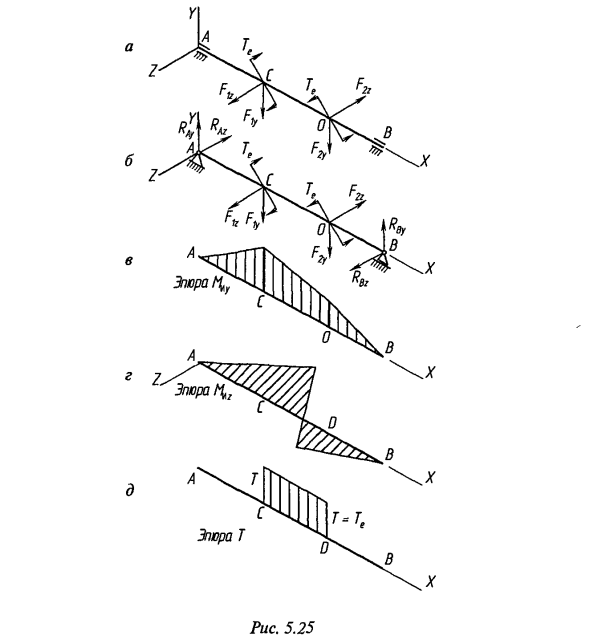
Деформация изгиба при кручении подвергается воздействию различных зубчатых валов. Расчет прочности вала при эксплуатации Эти деформации называются расчетами статической прочности для максимального усилия. На рис. 5.25 показана схема нагрузки, действующая на двухопорный вал. Для удобства расчета внешняя сила пространственной системы выражается в виде сил, вызывающих изгиб одновременно в вертикальной (F \ y, F2>) и горизонтальной (F [v F2z) плоскостях. Вал считается статически определяемым стержнем (рис. 5.25, б). Аналогично, реакция носителя определяется в виде мешалки, действующей в вертикальной (RL, RBy) и горизонтальной (R ^, RBz) плоскостях.

Крутящий момент T, равный внешнему крутящему моменту Te, действует на сечение вала CD в поперечном сечении. Под действием нагрузки, приложенной к секции, в секции возникают напряжения, нормальные к изгибу, и касательные напряжения от изгиба и скручивания. Величина напряжения сдвига из-за изгиба игнорируется. Это потому, что это не важно по сравнению с величиной напряжения сдвига из-за кручения. Используя принцип независимого действия силы, создайте диаграмму изгибающего момента от нормальной силы (рис. 5.25, в) и горизонтальной силы (рис. 5.25, д) и диаграмму крутящего момента (рис. 5.25, д) ,

• Сравнение построенных рисунков показывает, что разрез через точку C является наиболее опасным. В этом разделе, помимо крутящего момента, действует изгибающий момент. MH = jM2y + M2z. Известно, что максимальное нормальное напряжение при изгибе является предельным волокном и равно <5 = MJ \ V = jMly + Mll / wy Где W ~ 0, \ d3 — осевой момент сопротивления поперечного сечения в форме круга диаметром d. Максимальное касательное напряжение при кручении возникает в точке сечения, наиболее удаленной от центра, и определяется как: x = T / Wp-T / (2fV), Где Wp — полярный момент сопротивления сечения. В случае круга Wp = 0,2d3. Подставьте значения o и t в уравнения (5.46) и (5.47) и отметьте условия прочности вала при использовании третьей и четвертой гипотез о прочности соответственно.

o красный = l / Mi + r 1 fw <oadm; (5.48) _ / = jM * + 0.75T2 / lV <ca (Джм, (5.49) Где Гадм — допустимое натяжение материала вала под натяжением. Из уравнений (5.48) и (5.49) можно найти значение осевого момента сопротивления сечения вала: W + Т2 / oadm Или W + 0,75G2 / кадм, тогда диаметр вала: d ZlJW / 0,1

Смотрите также:

Решение задач по прикладной механике

Определение деформаций при изгибе	Концентрация напряжений
Понятие о теориях прочности	Контактные напряжения

Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.