Оглавление:


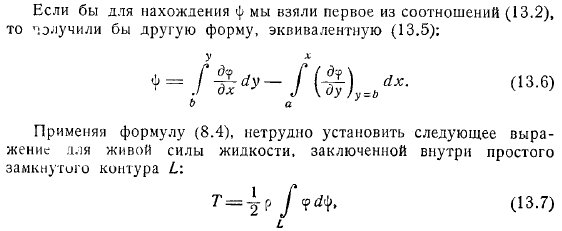
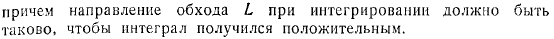

Связь функции тока с потенциалом скорости
Если существует потенциальная скорость в плоском движении, то существует уравнение, которое сравнивает их: последнее соотношение показывает, что каждая кривая семейства пересекается под прямым углом с кривой семейства линии. Обтекаемая линия является ортогональной траекторией семейства эквипотенциальных линий. Все четкие формы плоского движения жидкости интерпретируются четким рисунком распределения кривых в плоскости.
Поскольку кривые этих семейств ортогональны друг другу, геометрически безразлично, какая из них считается линией потока, а какая — эквипотенциальной кривой. Исходя из этого, функции называются сопряженными, и если удается найти решение конкретной плоской гидродинамической задачи, то есть если удается выбрать потенциал скорости, то в случае определенного граничного условия она одновременно приобретает другое плоское решение задачи. Текущие функции. Используя условие из сопряженных функций можно легко представить в терминах других функций.
Изолинии функции тока совпадают с линиями тока жидкости. Для стационарного (не зависящего от времени) течения они также являются траекториями частиц. Людмила Фирмаль
Факт, например, если известен потенциал скорости, то для нахождения функции потока достаточно получить из соотношения. Например, если вы берете значение и интегрируете в диапазоне от значения до получается. Являются неопределенными функциями. Чтобы найти последнее, достаточно сделать производную относительно: или первое соотношение, так как потенциал удовлетворяет уравнению Лапласа, то она становится.
Интеграл от конкретного значения до таков: поэтому, если мы возьмем, если мы возьмем первое отношение, мы получим другую форму, эквивалентную, а у формулы, простой замкнутый контур о движении жидкости, заключенной в, нетрудно установить следующую формулу: направление вокруг при интегрировании должно быть положительным для интеграла.
При некоторых условиях максимум функции тока равен расходу жидкости. Людмила Фирмаль

