Оглавление:







Метод преобразованного механизма
- Метод конверсионного механизма Методы преобразованного механизма, относящиеся к графоаналитику, могут быть использованы для определения линейной зависимости ошибки положения механизма от первичной ошибки. Он основан на идее построения схемы трансформируемого механизма и небольшого плана движения. Из уравнения (4.3):ASi = -—Aq ,, dqt Где E // E <7 — это функция, которая указывает влияние соответствующего первичной ошибки Aq {AS механизма на общую ошибку.
Но эта особенность E / _ AS, _ AS, At __ Sj dq, -Aq, At Aq (qt Его можно рассматривать как передаточное число или передаточное число (передаточное число) приводного звена и ведущего звена переделанного механизма. Преобразование механизма заключается в том, что ведущее звено фактического механизма фиксируется на месте, а звено, содержащее ошибку, имеет направление движения, соответствующее направлению изменения параметров исследуемого звена. Это становится ссылкой. Если передний канал преобразованного механизма информируется о скорости, пропорциональной основной ошибке механизма, подчиненный канал получает скорость, пропорциональную конкретной ошибке.
Следовательно, небольшой план движения для преобразованного механизма строится так же, как и план скорости. Людмила Фирмаль
Из небольшого плана перемещения (плана скорости) преобразованного механизма определяется частичная ошибка в положении механизма из-за соответствующей первичной ошибки и передаточного числа между ними. Рассматриваемый метод может найти частичные ошибки в механизме A Si, часто не прибегая к компиляции очень сложных функций положения. Этот метод может быть применен к механизму с более низкой парой движения и более высокой парой движения (кулачковый механизм). Он используется для оценки влияния ошибки размера звена на механизм и ошибки кинематической пары.
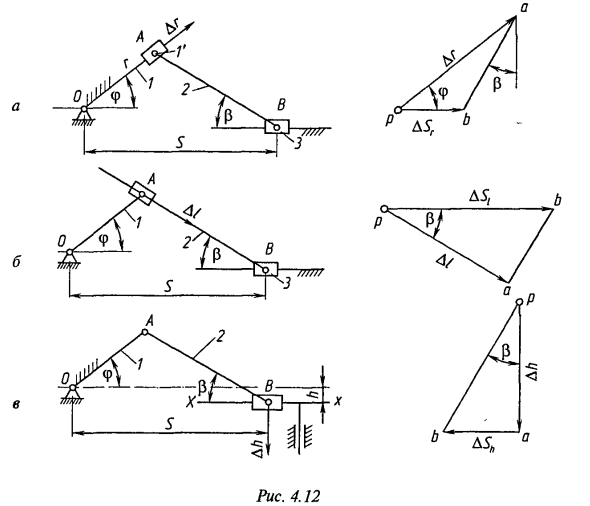
Пример 4.2. Рассмотрим применение метода механизма преобразования на примере механизма эксцентрикового кривошипного механизма (см. Рисунок 4.11). Ошибки механизма могут быть вызваны серьезными ошибками в размере кривошипа g, шатуна и эксцентрика I. Зафиксируйте верхнюю ссылку / и переместите дополнительную ссылку / ‘вдоль нее в направлении основной ошибки Ar. Направление ошибки Ar от точки (полюса) p Зафиксируйте отрезок pa = Ar / μ на шкале μ и укажите скорость точки соединения A / ′. Скорость (перемещение) точки B звена 3 может быть выражена с учетом перемещения звена AB (vB = vA + vBA) и ползунка для направляющей (vB-vB0).
- Решите графически приведенное уравнение и нарисуйте отрезок от точки параллели к вектору vBA. Перпендикулярно соединению AB, от полюса /? — Прямая, параллельная направляющей ползуна. Отрезок pb на шкале равен частичной ошибке ASr = \ pb \ L Zpba = nf 2 + P и Zpab = n / 2 равны (f + P), поэтому отношение ASr_sin (7t / 2 — ((p + P)) _ cos ((p + p) Ar sin (ft / 2 + P) cosp Откуда COSP Аналитически значения AS / и Д ^ получены из небольшого плана смещения (рис. 4.12, б). Частичная ошибка AS / считается положительной.
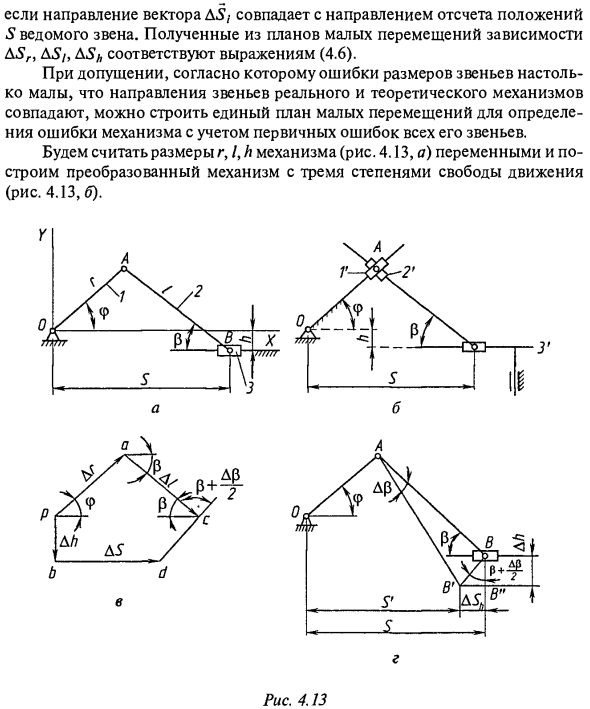
Зависимости A Sn A Si и A Sh, полученные из плана малых перемещений, соответствуют уравнению (4.6). Ошибка в размерах звеньев настолько мала, что ошибка механизма определяется с учетом основных ошибок всех звеньев в предположении, что направления звеньев действительного и теоретического механизмов совпадают. Вы можете построить единый план для небольших перемещений. Рассматривая размеры механизма r, f и h (рис. 4.13, а) как переменные, создайте преобразованный механизм с тремя степенями свободы (рис. 4.13.6). Рисунок 4.13
Направление вектора ASt совпадает с опорным направлением положения S подчиненного звена. Людмила Фирмаль
Создайте небольшую диаграмму смещения преобразованного механизма и скажите каждому звену небольшое смещение, равное Aq. Из точки (полюса) p (рис. 4.13, в) нарисуйте вектор pb, перпендикулярный направляющей ползуна 3 в направлении ошибки эксцентриситета эксцентриситета h, и на величину (| p £ | = DL / c) Сделать равным. Нарисуйте вектор pa от полюса p в направлении ошибки pa. Параллельно кривошипу и того же размера, что и ошибка длины Ar
Crank (| rd | = Lg / q). Нарисуйте вектор ac из точки a в направлении ошибки D /. Параллельно шатуну 2 и равна погрешности D / длина шатуна / (| ds | = D // t). Затем проведите линию, перпендикулярную шатуну 2 через точку c, и линию, параллельную направляющей ползуна через точку b. Выход bd представляет ошибку механизма AS. AS = \ bd \ L
Смотрите также:
| Задачи, решаемые при определении точности механизмов | Геометрический метод |
| Дифференциальный метод | Пути повышения точности механизмов |

