Оглавление:

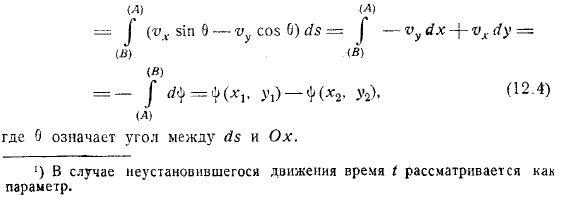
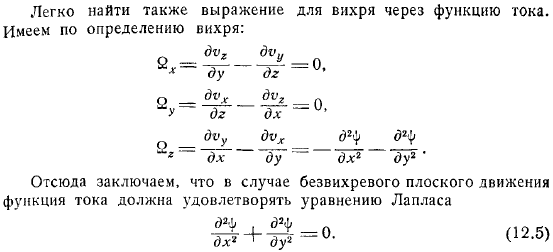

Функция тока
Не предполагая, что в жидкости нет вихрей, даже непрерывное уравнение может быть показано, чтобы наложить условие гидромеханики на поле скорости, которое может быть интерпретировано в плоском движении простым кинематическим. Факт, уравнение неразрывности дает несжимаемую жидкость.
Принимая дифференциальное уравнение линии потока или, уравнение неразрывности указывает, что левая часть последнего уравнения является полной производной функции плоского безвихревого движения называется потоковой функцией. Это должно поддерживать константу на каждой линии потока.
Как любой потенциал, функция тока определена с точностью до аддитивной постоянной. Людмила Фирмаль
Значение. Если кривая нарисована между точками, то легко увидеть, что поток жидкости через эту кривую представлен разностью значений функций потока в точках, независимо от формы. Факт, означает угол между. В случае переходного движения время считается параметром.
Вы также можете использовать функцию потока, чтобы легко найти уравнение. Определение связи функции тока с потенциалом скорости , есть вихрь. Таким образом, мы приходим к выводу, что для невращающегося плоского движения функция потока должна удовлетворять уравнению Лапласа.
Когда в задаче есть твёрдые стенки (на которых скорость равна нулю), то значение функции тока на них обычно принимается равной нулю. Людмила Фирмаль

