Оглавление:

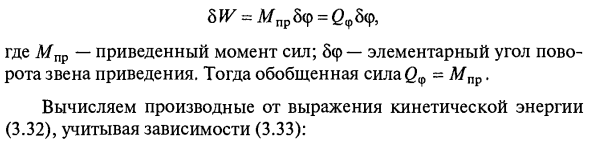

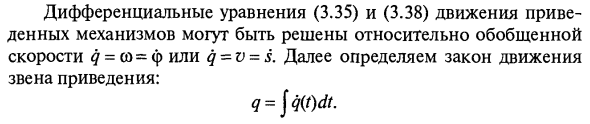


Уравнения движения приведенного механизма
- Уравнение движения редукторного механизма Механизм с одной степенью свободы является сложной динамической системой. Связь с определенной массой и моментом инерции нагружается многочисленными силами и моментами силы при движении. При выполнении динамического анализа такой механизм заменяется рассчитанной динамической моделью, состоящей из сокращенных связей. Энергетические параметры механизма и рассчитанная динамическая модель идентичны.
Параметры / pr и MPr являются функциями положения сокращенного звена, которое изменяется со временем. cf = f (0: (3,32) (3,31) Квадратичное уравнение Лагранжа (3.18) используется для получения уравнения движения для механизма редукции. Обобщенными координатами в этом случае являются угол поворота звена q = <p и обобщенная скорость q = <p = co.
Замедляющее звено совершает вращательное движение, так что момент инерции / pr уменьшается, а сила L / pr, действующая на него, уменьшается. Людмила Фирмаль
Кинетическая энергия механизма K = -Jupa2 = — / prF \ Где ω — угловая скорость звена замедления. Запишите второй вид уравнения Лагранжа в виде д дк ф (3.33) дт эф эф Обобщенная сила определяется из основного уравнения работы для всех сил, приведенных к звену редукции. 5 ^ = A / pr5 (p = Где MPR — момент уменьшения силы. Основной угол поворота 5av-link литой. Далее обобщенная сила <2ph = Mpr. Вычислить производную уравнения кинетической энергии (3.32) с учетом зависимости (3.33).
дк ^ 1,2 е / пр Ef 2 Ef Ef ge / pr Я эф е d_BK_ dt ef L * UI \ j-,. «R- = / prf + f Подстановка производной уравнения кинетической энергии (3.34) и обобщенной силы (? F) в уравнение (3.33) дает уравнение движения для звена замедления, которое выполняет вращательное движение. Рассмотрим расчетную динамическую модель механизма, состоящего из уменьшенного звена с уменьшенной массой TP в точке приложения уменьшенной силы. Обобщенной координатой в этом случае является движение точки q = s. Кинетическая энергия механизма определяется по формуле K = ± mnpv2 = ± mnps \ (3.36) Где v = s — скорость точки приведения. Запишите второй вид уравнения Лагранжа в виде ± dK_dK dt ds ds Основная работа уменьшенной силы — SJK = / ^ pfo = 0.
Следовательно, оно представляет собой обобщенную силу Qs = Fnp. Получение соответствующей производной кинетической энергии (3.36) и подстановка ее в уравнение (3.37) дает:Дифференциальные уравнения движения редукторного механизма (3.35) и (3.38) могут быть решены для обобщенной скорости q = o) = φ или q-v-s. Далее определяют закон движения контрактной ссылки. q = jq (t) dt Используя известные кинематические функции, если вы знаете эту функцию, вы можете рассчитать параметры движения звена привода механизма. Если приведенный момент инерции / pr и приведенная масса spr равны или близки к постоянному значению, уравнения (3.35) и (3.38) принимают вид: пр дт -‘пр DV MNN- Делать)
Смотрите также:
| Приведение сил и моментов сил | Коэффициент полезного действия механизмов |
| Приведение масс и моментов инерции | Ошибки механизмов и их деталей |

