Приведение масс и моментов инерции

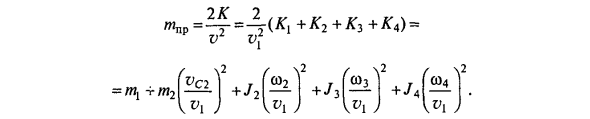
Приведение масс и моментов инерции

• Приносит массу и момент инерции Уменьшение массы TPR представляет собой условную массу, сосредоточенную в точке восстановления A и обладающую кинетической энергией, равной кинетической энергии механизма. K = mnpv2A / 2. так mpr = 2 K / v2a. Приведенный момент инерции является условным моментом инерции звена уменьшения вращения и имеет кинетическую энергию, равную кинетической энергии механизма. * = / prco £ p / 2. Если ^ = o> pr / 0/4, результат будет следующим: , Ls> = 2K / <i1p = / yp Где К — кинетическая энергия механизма. sopr — угловая скорость литого звена.

Уменьшение массы и уменьшение момента инерции характеризуют инерцию и скорость механизма. Кинетическая энергия механизма равна сумме кинетических энергий звеньев. Если механизм состоит из n звеньев, \ переводит, n2 вращается вокруг фиксированной оси, а n3 выполняет плоское параллельное движение, кинетическая энергия механизма вычисляется как \ mkV2CkJCk® / = 1 2 j = \ 2 к-л Где т — масса ссылки. Vq — скорость центра тяжести звена. J0j — момент инерции звена j относительно оси вращения O. co — угловая скорость звена. JCk — момент инерции звена k относительно центра тяжести C.

10А — расстояние от точки отливки до оси вращения литой связи. Людмила Фирмаль

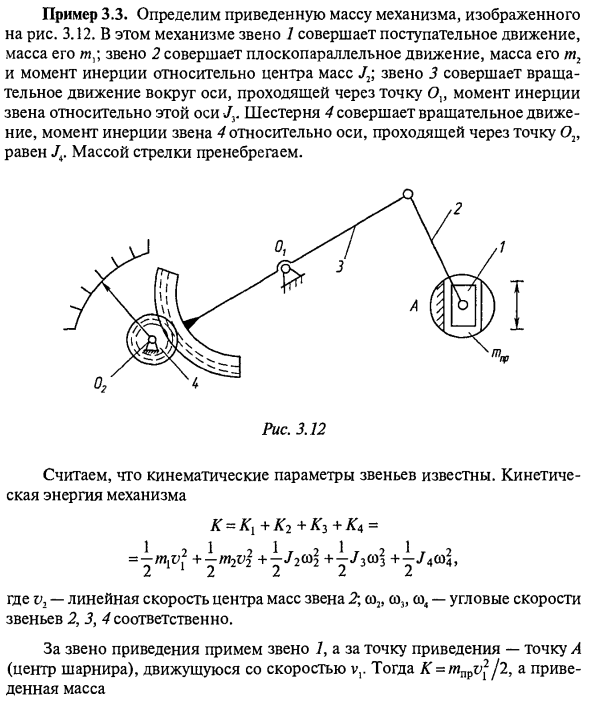
Определим убывающую массу механизма, изображенного в примере 3.3. 3.12. В этом механизме ссылка 7 выполняет поступательное движение, его масса / л. Звено 2 выполняет плоское параллельное движение, его масса m2 и момент инерции относительно центра тяжести J2. Звено 3 вращается вокруг оси, проходящей через точку Ov, момент инерции звена Jv шестерни 4 вокруг этой оси вращается, а момент инерции звена 4 относительно оси, проходящей через точку 02, равен / 4. Масса стрелы игнорируется. Рисунок 3.12 Мы считаем, что параметры движения звена известны. Кинетическая энергия механизма k = k1 + k2 + k2 + kA = -m {vl m2v \

Где v — линейная скорость центра тяжести единицы 2. co2, co и co4 — угловые скорости единиц 2, 3 и 4 соответственно. Звено 7 используется для звена замедления, а точка A (центр шарнира), движущаяся со скоростью v, используется для точки замедления. Тогда K = mnpv \ j2, и приведенная масса IT v \ / попса в \ 2 Vc2 + L Ш2 \ В Я ж в

Смотрите также:

Предмет прикладная механика

Метод приведения в динамике механизмов	Уравнения движения приведенного механизма
Приведение сил и моментов сил	Коэффициент полезного действия механизмов