Оглавление:


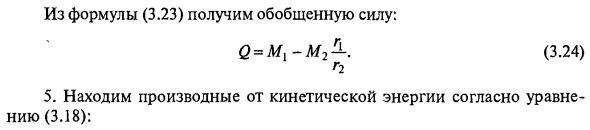


Методика составления уравнений Лагранжа второго рода
- Метод компиляции уравнения Лагранжа второго рода Квадратичное уравнение Лагранжа является дифференциальным уравнением второго порядка относительно обобщенных координат механической системы qx. Дифференциальное уравнение движения системы. Интегрирование их и определение постоянной интегрирования из начальных условий дает уравнение движения системы в обобщенных координатах. ? / =? / (‘) </ = 1,2, Вт). При составлении уравнений Лагранжа рекомендуется следующая последовательность операций. 1) Все активные силы, действующие на звено, показаны на схеме механизма.
3) Рассчитать кинетическую энергию механизма и выразить ее с помощью обобщенных координат и скорости. 4) Определить обобщенную силу механизма. 5) Выполнить дифференцирование кинетической энергии в соответствии с уравнением Лагранжа (3.18). 6) Подставьте полученную формулу в уравнение Лагранжа, чтобы определить целевой параметр.
Определить количество степеней свободы механизма и ввести обобщенные координаты. Людмила Фирмаль
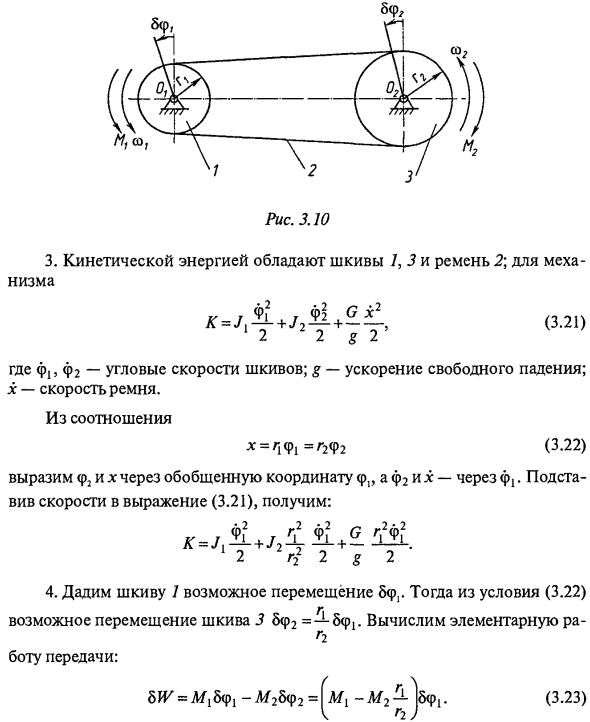
Пример 3.1 Передача вращения между двумя валами (рис. 3.10) представляет собой гибкое звено (ремень) 2. Если крутящий момент М действует на него и воздействует на другой момент сопротивления вала Mv, трение подшипника игнорируется моментом инерции вала. Решения. 1. Подайте моменты Mx, Mv и L / на шкив / и на три шестерни, направьте их в направлении вращения и M2 в противоположном направлении. 2. Коробка передач имеет одну степень свободы (один основной шкив-шкив 7). В обобщенных координатах получим угол поворота ведущего шкива. ? = F г
Рисунок 3.10 3. Механизм шкива 7, 3 и ремень 2 \ имеют кинетическую энергию *. / D + y2F1 + £ 11 (3,21) 1 2 2 2 с 2 Где f19 f2 — угловая скорость шкива. g — гравитационное ускорение. я скорость ремня. От отношений l = r1f1 = r2f2 (3,22) Представляет φ2 и π. Подставляя скорость уравнения (3.21) для φ2 и i с обобщенными координатами φα, это делается следующим образом. K = j 1 2 г 22 2 г 2 4. Дайте шкиву 7 возможное смещение 5 <pG. Тогда из условия (3.22) в Возможное смещение шкива 3 3 5f2 = -5f1v В Отправить бот: 5Ж = M15f1-L / 25f2 = (3,23)
Получите обобщенную силу из уравнения (3.23). Q = Ми-М2 ^ (3,24) 5. Найти производную кинетической энергии согласно уравнению (3.18). дк. , Д 2. G 2. 0Ф1Г2 £ ^ EA «r .. R \ G 2-s / φ1r2 £ (3,25) = 0 ДК Эф, 6. Подставим производную (3.25) и обобщенную силу (3.24) в уравнение Лагранжа второго порядка (3.18). G2 g G2 Отсюда найдите угловое ускорение первого вала. (3,26) 7 г ртО2 J + у24 + _г2 г2 г 1 Зависимость <Pi = <PiC) может быть получена путем интегрирования уравнения (3.26) дважды.
Смотрите также:
| Кинетическая энергия | Метод приведения в динамике механизмов |
| Обобщенные силы механизмов | Приведение сил и моментов сил |

