Модель роста Солоу

Модель роста Солоу

• Модель низкого роста В факторной модели Роберта Торо экономический рост определяется накоплением капитала, ростом рабочей силы и технологическими изменениями. Ниже приведена еще одна модель, разработанная Торо. Это показывает связь между сбережениями, накоплением капитала и экономическим ростом.

• Солоу впервые описал эту модель в 1956 году, но до сих пор был основной теоретической основой для анализа связи между сбережениями, накоплением капитала и экономическим ростом. Описание модели Отправной точкой анализа по-прежнему является производственная функция, выраженная уравнением (18.2).

Однако на этот раз все переменные выражены в виде показателей на человека. Людмила Фирмаль

Предположим еще раз, что население и рабочая сила одинаковы, и производство на человека равно производству на одного работника. Объем производства Q / L на одного работника представлен q, а объем капитала на единицу труда K / L представлен k. Производственную функцию в уравнении (18.2) можно переписать в следующем формате: 24Z. Griliches, «Головоломка продуктивности и исследования и разработки: еще одно объяснение», журнал «Экономические перспективы», осень 1988 г. 15см М. Бейли и Р. Гордон.

«Деградация производительности, проблемы измерения, взрыв вычислительной мощности». Брукинг по экономической деятельности, № 2, 1988. 16 «Вклад в теорию экономического роста», ежеквартальный экономический журнал, февраль 1956 года. Заимствовал из курса в лекции в Уорике, чтобы расширить теорию роста Исследование Университета Солоу «Теория роста: Экспо» (Нью-Йорк и Оксфорд: Оксфордский университет) Press 1988). я-тт.

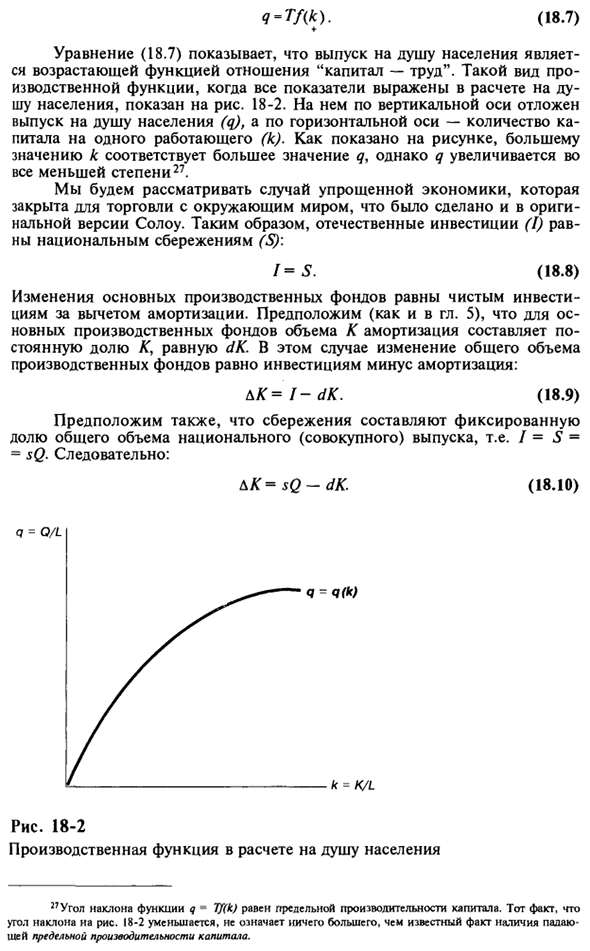
Уравнение (18.7) показывает, что производство на душу населения является возрастающей функцией отношений между капиталом и трудом. Этот тип производственной функции показан на рисунке, когда все показатели выражены на душу населения. 18-2. На вертикальной оси показана выработка на человека (q), а на горизонтальной оси показана сумма капитала на одного работника (k).

Как показано на рисунке, чем больше значение k, тем больше значение q, но тем меньше увеличение q27. Рассмотрим случай упрощенной экономики, закрытой для торговли с внешним миром в исходной версии Solow. Таким образом, внутренние инвестиции (I) равны внутренним сбережениям (S) \ (18,8) Изменение основных средств равно чистым инвестициям за вычетом износа.

Для основных средств тома K (как в главе 5) мы предполагаем, что амортизация представляет собой постоянный процент K, равный dK. В этом случае изменение общей суммы производственных активов равно инвестициям за вычетом износа. D K = I-dK. Предполагается также, что сбережения составляют фиксированную долю (общего) объема производства страны. / = S = sQ.

Поэтому: BK = sQ-dK. Q = 0 / л (18,7) / = S. (18,9) (18.10) I = Q (к) Рисунок 18-2 Производственная функция на человека к = к / л «Угол наклона q-Tf (k) функции равен предельной производительности капитала. Тот факт, что угол наклона на рис. 18-2 уменьшается, больше, чем известный факт, что предельная производительность уменьшается. нет.

Разделив обе части этой формулы на общую производительность труда: ^ -q-dk. (18.11) Население растет с определенной скоростью l, что определяется биологическими и другими факторами, не входящими в модель, при условии, что темпы роста населения равны темпу роста рабочей силы и bL / L = n вы.

Прогресс равен нулю. Где k = K / L, поэтому скорость роста k равна: От D до LK d L D / G T-T-G-T- (1812) Следовательно, DK = (Dk / k) K + nK. Здесь деление обеих сторон уравнения на L дает ——- Да: + шт. L / Подстановка формулы DK / L в формулу (18.11) дает основную формулу для накопления капитала. bk = sq- (n + d) k. (18.13) Это важное уравнение показывает, что темпы прироста капитала на одного работника (DK) равны сбережениям на одного работника кв.

Мин (l ++ d) k. Далее рассмотрите выражение, которое вы получили, более тщательно. Темп прироста общей численности работников равен n. Необходимо обеспечить капитал k каждому новому работнику, используя определенную экономию на душу населения. Это количество шт. В то же время определенная сумма сбережений на человека должна использоваться для замены выбывшего капитала. Так же, как дк.

Следовательно, сбережения на душу населения в размере (n + d) k необходимо использовать только для поддержания соотношения капитала и труда на определенном уровне k. Капитал — это труд (т.е. q> 0). Сбережения, направленные на организацию работы, называются сбережениями, направленными на увеличение капитала (здесь слово «расширение» означает увеличение числа работников).

Сбережения, используемые для увеличения коэффициента прироста капитала, называются сбережениями, которые увеличивают коэффициент капитального труда (рост коэффициента капитального труда означает увеличение капитала на одного работника). Поэтому основное уравнение накопления капитала (18.13) гласит: Сбережения для увеличения соотношения капитала и труда = сбережения на человека — сбережения будут расширяться Capital.

Теперь рассмотрим понятие стабильного (стационарного) состояния или положение долгосрочного равновесия. В устойчивом состоянии величина капитала на одного работника достигает равновесного значения, больше не меняется и всегда остается на этом уровне. снова В результате, производство на одного работника также является стабильным (обратите внимание, что технические изменения не принимаются во внимание в настоящее время).

Таким образом, в установившемся режиме и k, и q всегда находятся на одном уровне. Для достижения устойчивого состояния необходимо, чтобы было достигнуто точное равенство сбережений на душу населения и сбережений для увеличения капитала и ДА: = 0. Формально это можно записать так: sq = (n + d) k. Устойчивое состояние означает, что q и k являются постоянными значениями, но скорость роста никогда не станет нулевой.

На самом деле, устойчивое состояние сопровождается увеличением выхода с положительной скоростью р. Чтобы подтвердить это, помните, что рабочая сила увеличивается (как обычно) со скоростью р. Следовательно, коэффициент капитального труда постоянен, поэтому DK / K = DL / L = n. Поэтому количество производственных активов также увеличивается со скоростью n.

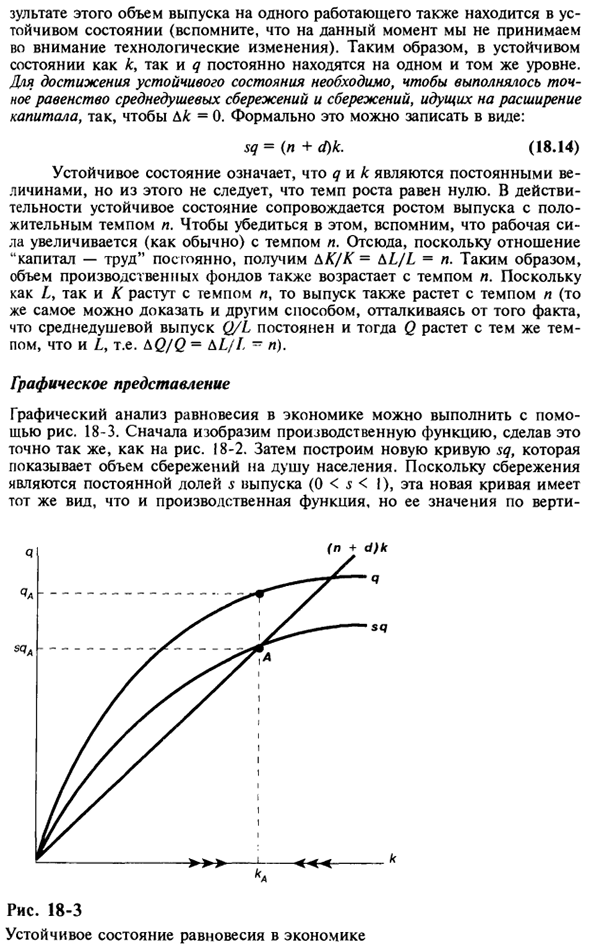
Поскольку и L, и K увеличиваются со скоростью n, выход также увеличивается со скоростью n (то же самое, выход на человека Q / L постоянен, Q такой же, как Z ДQ / Q = ДL / L ~ n). Графическое представление Вы можете использовать диаграмму для графического анализа экономического равновесия. 18-3. Сначала проиллюстрирована производственная функция. Это точно так же, как на рисунке 1. 18-2.

Затем создайте новую кривую sq, которая показывает сумму сбережений на человека. Поскольку экономия составляет постоянный процент от выпуска s (0 <s <1), эта новая кривая имеет ту же форму, что и производственная функция, но ее значение является вертикальным (18.14) (N + d) k Q Рисунок 18-3 Экономическое равновесие к Для стальных валов соответствующее значение производственной функции является дробным s.

Так как s <1, новая кривая находится под производственной функцией. iMu также может нарисовать линию (n + d) k — это линия через начало координат под углом (n + d). В установившемся режиме sq = (l + d) k, поэтому линия (n + d) k и кривая sq должны пересекаться. Пересечение этих кривых на рисунке — точка А. Если соотношение «капитал-труд» равно kAu, а объем производства на душу населения равен qA>, сумма, необходимая для расширения капитала, то есть sqA = (n + d) kA.

• В этом случае средняя экономия на одного человека достаточна для обеспечения новых рабочих мест и замены пенсионного капитала без изменения общего отношения капитала к труду. (Важно отметить, что устойчивое состояние является только «стабильным» по отношению к переменной на душу населения. В устойчивом состоянии агрегированные показатели (производство, рабочая сила, капитал) растут со скоростью, равной p. ты с.)

Кривая sq в левой части точки A выше кривой (n + d) k. Это означает, что сбережений больше, чем необходимо для увеличения капитала. В результате в левой части пункта А отношение капитала к труду увеличилось. Это означает, что производственные активы на одного работника увеличиваются и k> 0. Поэтому в левой части точки A ku, обозначенное стрелкой на оси X, имеет тенденцию к увеличению.

В этом случае одних только сбережений недостаточно для расширения капитала. Людмила Фирмаль

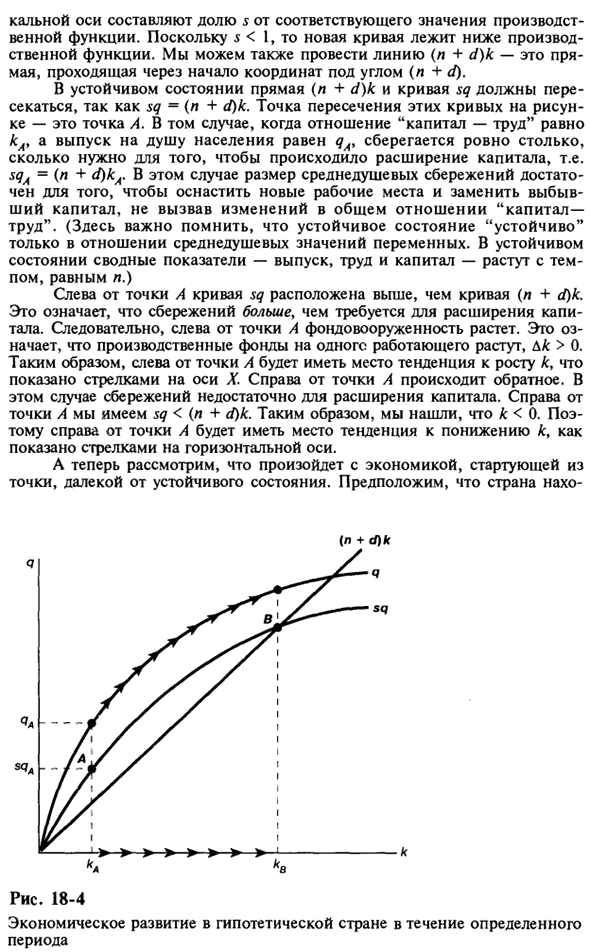
Справа от точки A находится sq <(n + d) k. Итак, мы обнаружили, что к <0. Следовательно, справа от точки A наблюдается тенденция к снижению k, о чем свидетельствует горизонтальная стрелка. Далее давайте рассмотрим, что происходит в экономике, начиная с точки, далекой от устойчивого состояния. страна (L + d) k Рис. 18-4 Экономическое развитие виртуальной страны в течение определенного периода времени.

Это происходит на ранней стадии экономического развития и имеет очень низкое соотношение капитала и рабочей силы, например, равное kA, как показано на рисунке 1. 18-4. Начальный выход на человека очень низкий, кА. Из-за небольшого количества производительных активов необходимость прямого сбережения для увеличения капитала мала, т. Е. (N ++ d) кА мала.

Следовательно, экономия на душу населения равна sqA>, что превышает потребность в увеличении капитала, и производительность капитала растет. Выпуск q на одного работника также увеличивается. Экономика движется вправо от А вдоль графика производственной функции.

В то же время, подход к #. По мере того как отношение капитала к труду увеличивается, количество капитала, необходимого для расширения, то есть для обеспечения новой работы и замены выбывшего капитала, со временем будет увеличиваться, и в конечном итоге все сбережения будут оставаться постоянными. Дойти до точки, чтобы идти только для поддержания. На данный момент экономика стабильна.

Каковы темпы экономического роста в период, когда экономика движется к стабильности? Обратите внимание, что и q, и k увеличиваются со временем, когда экономика находится в фазе роста соотношения капитала и труда. Q / L и K / L приближаются к значениям в устойчивом состоянии. Поскольку Q / L растет, Q растет быстрее, чем L. Следовательно, D (> / (?> DL / L = n. Это означает, что в период роста коэффициента капитального труда темпы роста выпуска выше, чем в устойчивом состоянии.

Проще говоря, мы ( при прочих равных условиях) можно ожидать, что страна с низкой пропускной способностью будет расти быстрее, чем страна, богатая капиталом, и темпы роста будут снижаться по мере увеличения отношения капитала к труду (ближе к q). Если k превышает k, легко увидеть, что величина капитала на одного работника уменьшается до уровня, соответствующего устойчивому состоянию. (Это должно стать ясным после рассмотрения направления стрелки на рисунке 18-3.)

В этом случае одних только сбережений недостаточно, чтобы поддерживать постоянную связь между капиталом и трудом. Обратите внимание, что если коэффициент капитального труда падает в богатой капиталом стране, темпы роста производства будут ниже, чем p. Таким образом, мы установили, что, если экономика не находится в стабильном состоянии, независимо от количества капитала на одного работника, начинают действовать силы, которые приводят к долгосрочному устойчивому равновесию.

Эта особенность модели Солоу очень важна. Это происходит не только потому, что стабильное состояние состоит в том, что q и k не меняются, но и потому, что было доказано, что оно приводит экономику к стабильному состоянию в ее естественном состоянии. Динамическая система, характеристики которой автоматически возвращаются в устойчивое состояние равновесия, называется устойчивой системой.

Таким образом, модель роста Солоу представляет собой стабильный и динамичный процесс роста. Влияние сбережений на доходы и экономический рост Очень часто странам, которые хотят ускорить экономический рост, рекомендуется увеличивать свои сбережения. Это правда Способствуют ли более высокие уровни сбережений ускорению экономического роста?

Да нет Это может удивлять, но в модели Солоу уровень экономии не влияет на устойчивый рост. Независимо от важности j, в долгосрочной перспективе экономика будет расти со скоростью p, но уровень сбережений будет Влияние на краткосрочный экономический рост и долгосрочный устойчивый средний доход на душу населения. Давайте снова воспользуемся таблицей для более детального изучения этой проблемы.

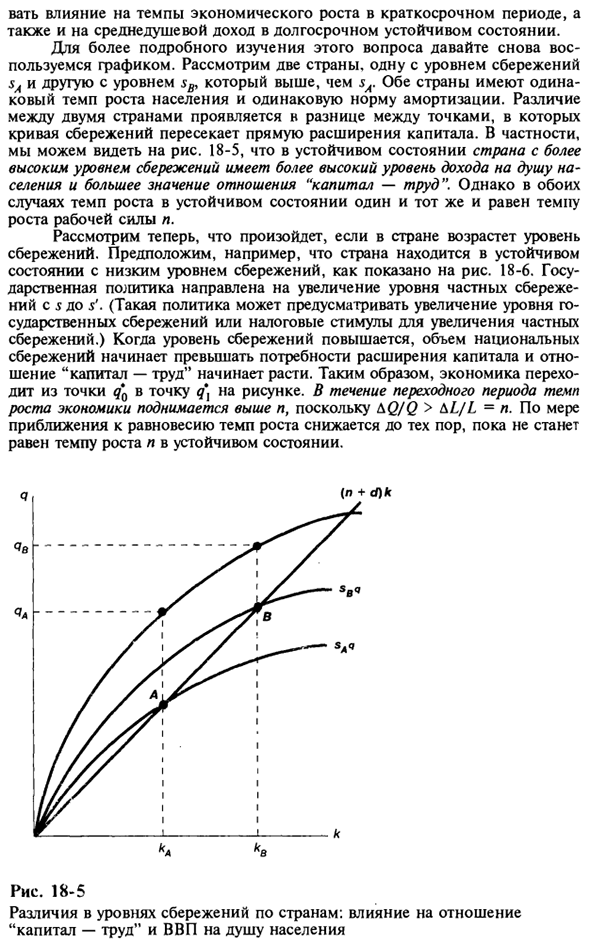
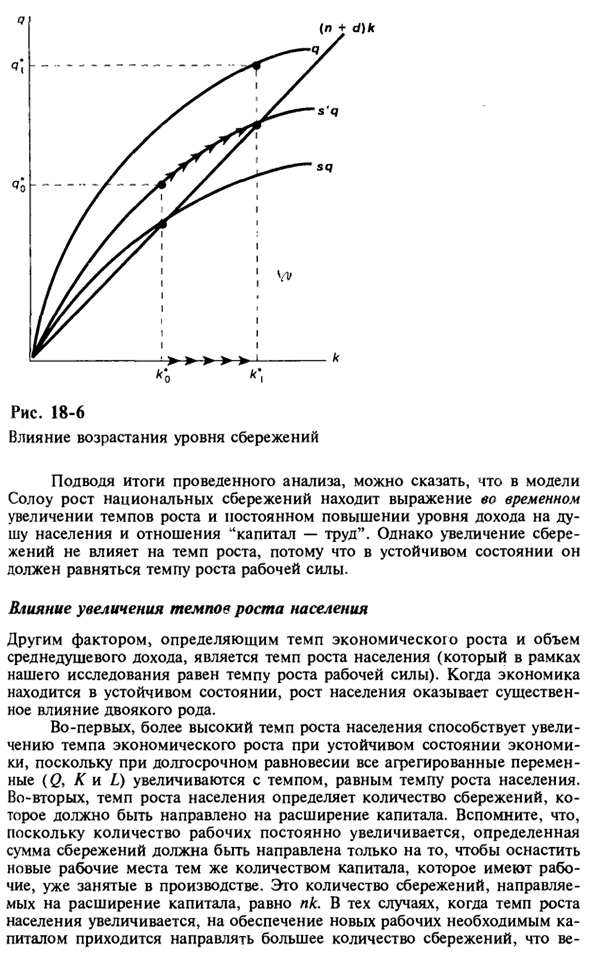
Рассмотрим страну с уровнем сбережений sA и страной с уровнем sB выше, чем sA. Темпы роста населения и износа в обеих странах одинаковы. Разница между двумя странами отражается в разнице между кривой сбережений и прямым расширением капитала. В частности, вы можете увидеть на рисунке. 18-5. В устойчивом состоянии, чем выше уровень сбережений, тем выше уровень дохода на душу населения и тем выше значение отношений между капиталом и трудом.

Однако в обоих случаях стационарные темпы роста одинаковы и равны темпу роста рабочей силы. Теперь давайте рассмотрим, что происходит, когда уровень сбережений в стране увеличивается. Например, предположим, что страна стабильна, а уровень сбережений низкий (см. Рисунок 1). 18-6. Государственная политика направлена ​​на повышение уровня личных сбережений с с до с ‘.

Такая политика может включать налоговые стимулы для увеличения государственных сбережений или увеличения личных сбережений.) Следовательно, экономика перемещается от точки 9q к точке q \ на рисунке. В течение переходного периода & Q / Q> & L / L = n, поэтому темпы экономического роста вырастут выше n. Рис. 18-5 Различия в уровнях сбережений по странам: соотношение капитала и труда и влияние на ВВП на душу населения Рис. 18-6

Влияние увеличения сбережений Подводя итоги анализа, модель Солоу показывает, что рост национальных сбережений представлен временным увеличением темпов роста и постоянным увеличением дохода на душу населения и коэффициента капитального труда. Тем не менее, увеличение сбережений не влияет на темпы роста, потому что оно должно быть равным темпу роста рабочей силы в устойчивом состоянии.

Титания увеличение прироста населения Другим фактором, определяющим экономический рост и величину дохода на душу населения, является темп прироста населения (в данном исследовании он равен темпу роста рабочей силы). Когда экономика стабильна, рост населения имеет два эффекта.

Во-первых, в долгосрочном равновесии все общие переменные (Qy K и L) увеличиваются со скоростью, равной темпу прироста населения, поэтому чем выше темп прироста населения, тем выше темп экономического роста в стабильной экономике. Во-вторых, темпы роста населения определяют сумму сбережений, которая должна быть направлена ​​на увеличение капитала.

Поскольку число работников постоянно увеличивается, некоторые сбережения должны быть направлены только на то, чтобы дать новым рабочим местам тот же объем капитала, который имеют работники, уже занятые в производстве. Пожалуйста, не забывайте. Эта экономия, выделяемая на расширение капитала, составляет шт. По мере роста населения необходимо направлять больше сбережений для обеспечения необходимого капитала для новых работников.

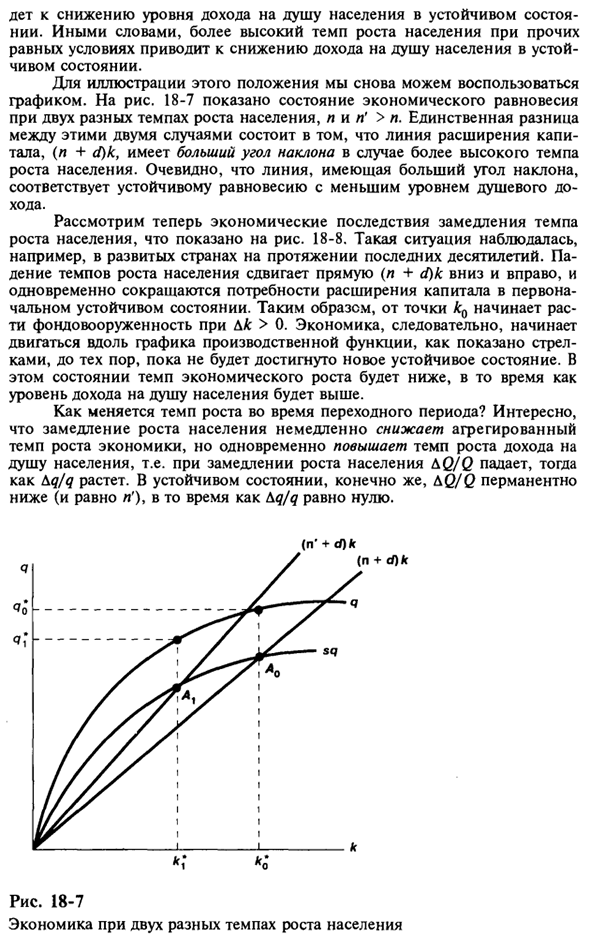
У детей доход на душу населения снижается в стабильном состоянии. Другими словами, если все остальные условия одинаковы, чем выше темп прироста населения, тем ниже доход на душу населения в стабильном состоянии. График может быть использован снова, чтобы проиллюстрировать этот момент. Рисунок 18-7 показывает состояние экономического равновесия при двух разных темпах роста населения, lil ‘> l.

Единственное различие между этими двумя случаями состоит в том, что если темпы прироста населения высоки, наклон линии расширения капитала (l + d) k будет увеличиваться. Очевидно, что линия с большим наклоном соответствует устойчивому равновесию с низким уровнем дохода на душу населения. Рассмотрим экономический эффект замедления роста населения, как показано на рисунке. 18-8.

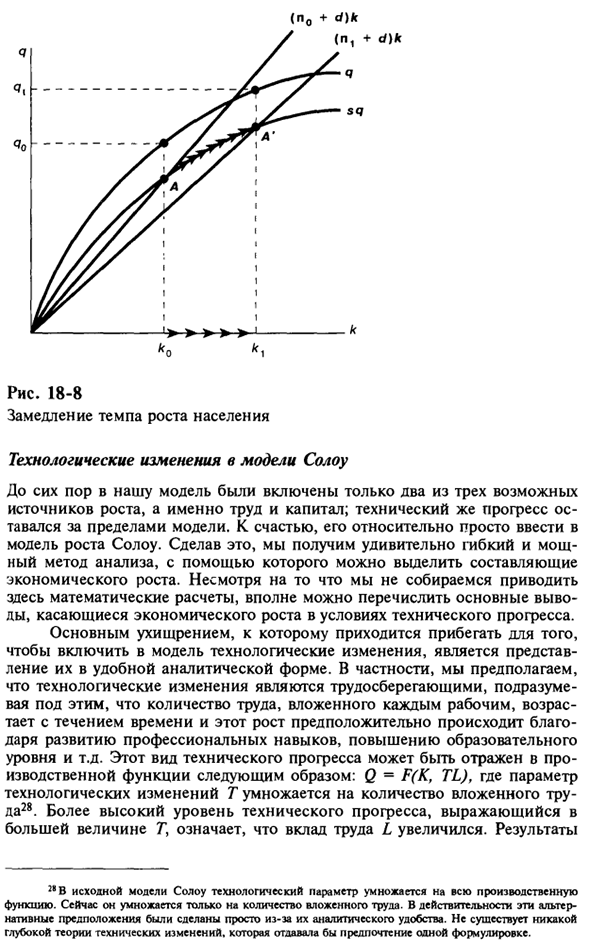
Такая ситуация наблюдалась, например, в развитых странах в последние десятилетия. Снижение прироста населения сдвигает прямую линию (l + d) k в нижний правый угол и в то же время уменьшает необходимость увеличения капитала в исходном устойчивом состоянии. Следовательно, с точки k0 отношение капитала к труду начинает расти с ростом DA. 0

Таким образом, экономика начинает двигаться по графику производственной функции, как показано стрелками, пока не достигнет нового устойчивого состояния. В этом штате темпы экономического роста низкие, а уровень доходов на душу населения высокий. Как изменится темп роста в переходный период?

Интересно отметить, что замедление роста населения сразу же снижает общие темпы роста экономики, но в то же время темпы роста доходов на душу населения, то есть при замедлении роста населения, DQ / Q уменьшается, а Dq / q увеличивается вы. В устойчивом состоянии, конечно, DQ / Q всегда низок (равен l ‘), а Dq / q равен нулю. (L ‘+ d) k Я (N + d) k Рисунок 18-7

Экономика с двумя разными темпами роста населения «О» Я (П0 + д) к Рисунок 18-8 Технологические изменения в медленной модели замедления роста населения До сих пор из трех возможных источников роста в модель были включены только два труда и капитала. Технический прогресс остался за пределами модели. К счастью, это относительно легко реализовать в модели роста Солоу.

Это обеспечивает удивительно гибкий и мощный метод анализа и может выделить элементы экономического роста. Несмотря на то, что здесь нет математических расчетов, вполне возможно перечислить основные выводы об экономическом росте в условиях технического прогресса. Основной трюк, на который вы должны полагаться при внесении технических изменений в модель, — представить их в удобном аналитическом формате.

В частности, изменения в технологии приводят к экономии труда, и объем работы, вкладываемой каждым работником, со временем увеличивается, и предполагается, что этот рост обусловлен развитием специализированных навыков и повышением уровня образования. Этот тип технического прогресса отражен в производственных функциях следующим образом:

Более высокий уровень технического прогресса, выраженный большим значением T>, означает, что вклад рабочей силы L увеличился. результат 14 В исходной модели Solow технические параметры умножаются на всю производственную функцию. Теперь умножается только количество вложенного труда. Фактически эти альтернативные предположения были сделаны исключительно для удобства анализа.

Не существует глубокой теории технологических изменений, которая бы поддерживала единую формулировку. Рабочее время каждого работника увеличивается на один час. Общий объем вложенного труда, определенный как TL, иногда называют эффективным вложением рабочей силы или просто эффективным трудом и обозначается как Le (e означает «эффективный»).

Предположим, что техническое изменение происходит с постоянной скоростью, равной нулю. A7CH / T-c. В этом случае эффективный темп роста рабочей силы равен n + c. Таким образом, эффективная рабочая сила растет по двум причинам: рост населения и повышение производительности труда на одного работника. Эффективный темп роста рабочей силы равен сумме этих двух темпов роста29.

В результате технологические изменения увеличивают экономический рост в устойчивом состоянии, поскольку он увеличивает скорость роста рабочей силы, измеряемую с учетом его эффективности. Вы можете использовать этот широкий подход, чтобы определить влияние технологических изменений на экономический рост. Основные выводы:

Если темпы технологических изменений в области экономии труда будут положительными, производство в устойчивом равновесии будет расти со скоростью p + p, равной сумме темпов роста рабочей силы и темпов технологических изменений. В устойчивом состоянии объем производства на одного работающего и капитал на одного работающего остаются неизменными.

Однако реальное производство рабочих и реальный рабочий капитал увеличиваются с той же скоростью, что и технологические изменения. Следовательно, темпы технологических изменений — это устойчивые темпы роста доходов на душу населения, то есть темпы роста объема производства на душу населения.

Смотрите также:

• Решение задач по экономике

Источники экономического роста	Новые подходы к объяснению экономического роста
Возможные объяснения замедления роста производительности в США	Экономический рост в открытой экономике

Если вам потребуется помощь по экономике вы всегда можете написать мне в whatsapp.