Критерии устойчивости Михайлова

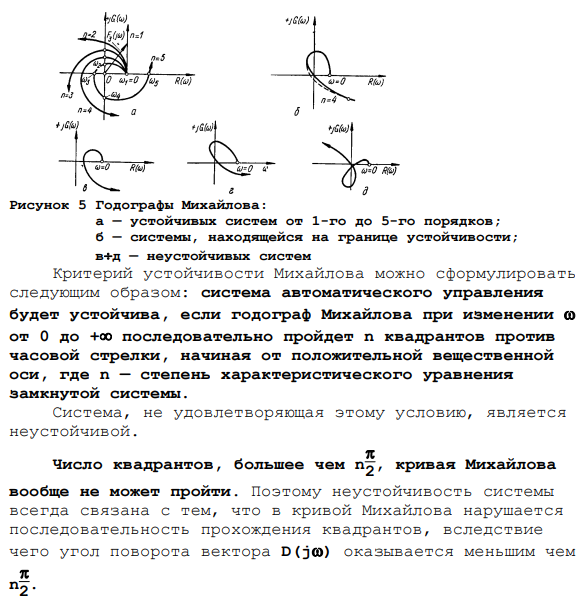
Критерии устойчивости Михайлова

По критерию Михайлова, предложенному А. В. в 1938 г., об устойчивости системы можно судить по кривой, построенной на основе характеристического полинома замкнутой системы. В системных уравнениях, замкнутых единичной обратной связью, характеристический полином является полиномом.

Существует общая форма нормализованного полинома. Как вы знаете, этот многочлен может вычислять корень характеристического уравнения замкнутой системы. Задача состоит в том, чтобы определить условие, когда все корни характеристического уравнения находятся слева от мнимой оси в частотной плоскости.

• В частотной плоскости каждый корень числа pi представлен либо точкой, либо вектором, проведенным от начала координат до этой точки. Изображение корня характеристического уравнения на комплексной плоскости в определении вектора по вектору. Векторное определение Текущая координата p, которая является комплексным числом, также геометрически представлена ​​в виде вектора.

Каждый фактор в выражении, который представляет собой разницу между двумя векторами, также является вектором, начальная точка которого находится в точке, определяющей маршрут, и конечная точка которой находится в точке, соответствующей текущим координатам. Выражение особенно полезно для текущего значения координаты p. Конец основного вектора в этом случае находится в точке на виртуальной оси, как показано на рисунке 4а, и движется вдоль этой оси при изменении ω.

Длина (модуль) и угол поворота каждого вектора изменяются. Общепринято, что вращение вектора против часовой стрелки является положительным. Когда вы изменяете, начало координат (то есть корень) поворачивается на угол + π с каждым базовым вектором в левой плоскости, а начало каждого вектора находится в правой полуплоскости.

Поскольку функция равна произведению базовых векторов, сама функция является вектором.

• Векторный модуль, называемый характеристикой, равен произведению базовых векторных модулей, а его аргумент является суммой этих векторных аргументов.

Изменение argD (jω) при изменении зависит от положения маршрута на частотной плоскости. Если все n корней характеристического уравнения замкнутой системы лежат в левой полуплоскости, соответствующей устойчивой системе, изменение ее изменит + nπ. То есть вектор вращается против часовой стрелки на угол nπ. Если хотя бы один корень характеристического уравнения отображается в правой полуплоскости, соответствующей нестабильной системе, вектор будет вращаться меньше, чем nπ, по мере его изменения.

На практике не нужно менять, просто меняйте. Характеристический многочлен имеет корень в правой полуплоскости, если фаза или полное приращение аргумента при изменении ω от 0 до ∞ равно порядку многочлена. В результате система регулирования стабильна. Если общее приращение аргумента мало, система нестабильна. Если указаны все коэффициенты и установлено конкретное значение частоты, это значение отображается в комплексной плоскости в виде точки с координатами или в виде вектора, соединяющего эту точку с началом координат. Когда значение частоты ω непрерывно изменяется от нуля до бесконечности, величина и направление вектора изменяются, и последняя кривая (годограф), называемая кривой Михайлова, записывается последней.

Видно, что кривая Михайлова устойчивой системы всегда имеет гладкую спиральную форму, конечная точка которой бесконечна в квадранте комплексной плоскости, а ее число равно порядку характеристического уравнения. Годограф Михайлова: Стабильная система от -1 до 5 порядка.

Система на границе устойчивости. Критерии устойчивости неустойчивой системы Михайлова можно сформулировать следующим образом: годограф Михайлова начинается с положительной вещественной оси, изменяется ω от положительной оси, степень характеристического уравнения замкнутой системы Система автоматического управления стабильна при прохождении через n квадрантов против часовой стрелки. Системы, которые не удовлетворяют этому условию, нестабильны. Число квадрантов, превышающих кривую Михайлова, вообще не может пройти.

Таким образом, нестабильность системы всегда связана с тем, что кривая Михайлова нарушает серию квадрантных проходов, что приводит к меньшему углу поворота вектора.

Фактически начальное представление характеристического многочлена замкнутой системы с заменой p используется для построения годографа Михайлова. На практике кривая Михайлова создается на основе точек, заданных с разными значениями частоты ω и рассчитываемых по формуле.

Результаты расчета сведены в таблицу, и соответственно создана кривая.

В этом случае вы получите характеристический комплекс, действительная часть которого содержит четную степень, а мнимая часть содержит нечетную степень. Из уравнения определяют частоту на пересечении действительной оси годографа Михайлова. Частота пересечения годографа мнимой оси определяется из уравнения.

Отрицательные корневые значения отбрасываются и вносятся изменения. Найденное значение присваивается выражению выражения. Определите пересечение годографа и координатных осей и создайте годограф. Когда система окажется стабильной. В этом случае отображается приблизительный вид годографа. Михайлов годограф третьей стабильной системы.

Смотрите также:

Решение задач по теории автоматического управления

GAP напряжения генератора постоянного тока. Математическое описание	Критерий устойчивости Найквиста
Определение устойчивости с помощью критерия гурвица	Критерий устойчивости Гурвица