Оглавление:

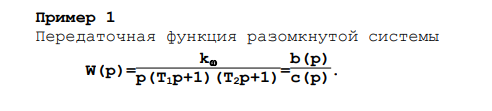




Определение устойчивости с помощью критерия гурвица
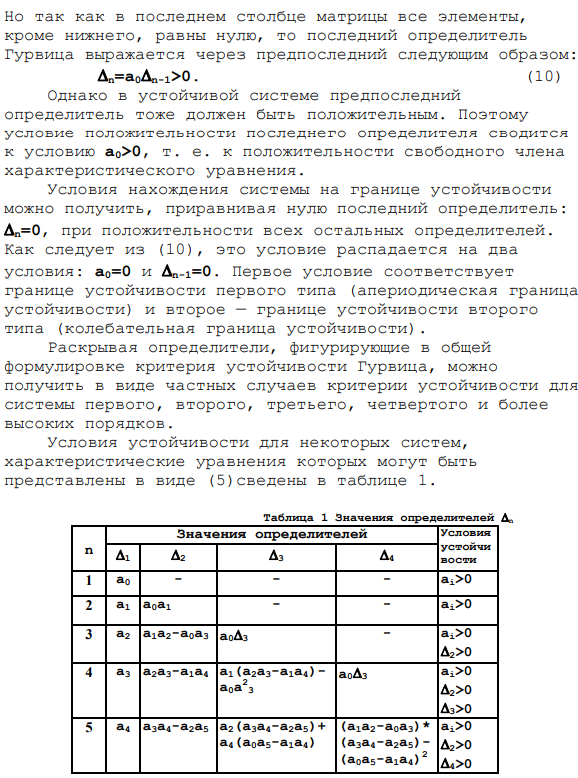
Критерий, предложенный немецким математиком А. Гурвицем в 1895 г., формируется следующим образом: все n-гурвицы так, что все корни нулевого характеристического уравнения n-го порядка имеют отрицательные вещественные части Необходимо и достаточно, чтобы определитель был больше нуля.
- При создании определителей Гурвица вы должны следовать следующим правилам.: Для уравнений n-го порядка необходимо определить n определителей. Последний (основной) определитель является n-м, предпоследним. Стандарт стабильности сам по себе. Определитель Гурвица выражается через предпоследнюю точку следующим образом:
Однако в стабильных системах предпоследний определитель также должен быть положительным.
Следовательно, положительное условие последнего определителя является положительным условием свободного члена характеристического уравнения. Условие нахождения системы на границе устойчивости можно получить, сделав последний определитель равным нулю, если все остальные определители положительны. Как видно из (10), это условие делится на два условия.
Первое условие соответствует первому типу границы устойчивости (апериодическая граница устойчивости), а второе условие соответствует второму типу границы устойчивости (граница устойчивости колебаний). Поясняя детерминанты, которые появляются в общей формулировке критерия устойчивости Гурвица, критерии устойчивости для систем первого порядка, второго порядка, третьего порядка, четвертого порядка и выше в особых случаях образуют вы можете получить это.
Некоторые условия устойчивости системы, которые могут быть выражены характеристическим уравнением в виде, представляют собой суммированное определяющее значение n определяющего значения.
Пример , передаточная функция открытой системы. В открытом состоянии система нейтрально нейтральна (корень характеристического уравнения для (p) = 0 равен нулю). Критерий Гурвица должен использоваться для определения условий, при которых замкнутая система стабилизируется отрицательной обратной связью устройства.
- Решения характеристические уравнения для замкнутых систем. Согласно таблице, необходимы и достаточны условия для устойчивости. Графически это состояние показано на рисунке. Кривая, содержащая уравнение, называется границей устойчивости.
Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительными. Определитель Гурвица составляется в соответствии с коэффициентами характеристического уравнения.
Для этого все коэффициенты в характеристическом уравнении записываются на основную диагональ делителя, начиная со второго, причем коэффициент увеличивается в индексе вверх, а индекс уменьшается вниз.
Например, в случае третьего коэффициента в главной диагонали они записываются вверх и вниз (увеличение индекса). Остальные оставшиеся места равны нулю. Чтобы проверить точность записи определителя Гурвица, вы должны учитывать тот факт, что коэффициенты с нечетными и четными индексами чередуются в строках. Таким образом, первая строка нечетная вторая строка.
Смотрите также:
Решение задач по теории автоматического управления
| Нестационарные линейные системы | Критерии устойчивости Михайлова |
| GAP напряжения генератора постоянного тока. Математическое описание | Критерий устойчивости Найквиста |

