Оглавление:













Гетерогенные многокомпонентные системы
- Гетерогенные композиционные компонентные системы В термодинамике понятие фазы означает однородную подсистему, окруженную поверхностью с резким изменением физических свойств matter.At граница раздела между жидкими фазами, этот разрыв в непрерывности свойств вещества может исчезнуть в критическом состоянии. рассмотрим компоненты, распределенные в фазе p.Потенциал гибкости такой системы должен быть равен сумме вкладов различных фаз Г = 2Г (РЛ.(6.62) г-1.
Для каждой фазы, как в Формуле (6.43), (6.46) и (6.47) с <ф)=±п (; ВП,я-1 dGlr)= — С (Р) ДТ + в (р) ДП + Ф <Р) дн (Р, (6.63) НФ dyif = — ДТ-Ф-ДП. Это получается из условия (6.9) — в равновесном состоянии химический потенциал\ xt всех компонентов должен быть постоянным во всей системе, но для того, чтобы сделать дальнейшие выводы, необходимо выразить это с помощью более общего метода. Чтобы уравновесить с константой 7 \ P, нам нужно (bG) T p> 0 для изменения состава одной из фаз.То есть, согласно (6.63)、 6.0 = 2 ш; Р)6 / В(Р)= 0 (6.64) От Юу В этом отношении вариация Λ (Γ(Γ) не является независимой, а условной 26 / Vf = 0, / =1,2…..С. (6.65)) {П
Итого Молекулы каждого типа во все времена: С. С. 2 bL / f) = Ni (полный) = const (6.66) г-1. (Процесс, в котором молекула возникает или исчезает, не рассматривается here.In дополнение к уравнению вариации (6.64) должно удовлетворять дополнительным условиям (6.65).Обычным решением является использование метода лагранжевых факторов.Умножьте каждое уравнение (от 1-го до s-го) на постоянный коэффициент, на| .И2,…, Вычтем из (6.64), это выглядит так: 1±(НГ-ч,.) ба / ^ = 0, (6.67) g = 1 4 7 Здесь вариации можно рассматривать как независимые и произвольные.Продолжать. = Джо., = = Общесистемный const,/ = 1, 2 ….. С. (6.68))
Таким образом, фазовый индекс (/ *) y \ x в равновесном состоянии избыточен. Людмила Фирмаль
Однако, r = 1, 2,…Не забывайте, что p представляет различные функции температуры, давления и состава. 1.Правила фаз Гиббса. § 2, в пункте 1, мы обнаружили, что для чистой материи максимальное число фаз, которые могут сосуществовать в равновесии, равно 3.Это частный случай следующих общих правил, установленных Гиббсом в первую очередь. просмотрите компоненты, которые распределены в p-фазе again.In равновесное состояние, термодинамический потенциал каждого компонента должны быть равны во всех фазах, и получено уравнение Р-1 ^ 1)= [A(2)= _ =(6 <69) в компоненте c необходимо удовлетворять только c (p-1)такого уравнения.Количество независимых переменных? * )
См. Приложение B. Если вы выберете температуру, давление и молярную фракцию в качестве параметров, вы получите 2 переменные ПК.Однако не все эти переменные являются independent.In каждая фаза согласно определению молярной фракции (6.44) 2 мг)= 1.(6.70) / = 1 Поэтому только параметр 2 — \ — pc-p является по-настоящему независимой переменной.Если число уравнений (6.69) превышает число переменных, которые могут быть произвольно изменены, то система уравнений не имеет решения.То есть, невозможно уравнять с таким большим количеством фаз.Если число уравнений равно числу независимых переменных, то существует единственное решение для тех же температуры, давления и фазового состава.Наконец, если число фаз очень мало, а число свободных параметров больше числа уравнений, то равновесие возможно для некоторого множества состояний.
- Превышение этого параметра называется числом термодинамических степеней свободы. Согласно расчетам, описанным выше、 2-f-pc-p-число независимых переменных, pc-c-число уравнений, f — 2 — \ — c-p-число степеней свободы、 Правила могут быть сформулированы.Число фаз и число степеней свободы системы равно числу составляющих плюс 2. Для чистого вещества, c = 1.So, максимальное значение p равно 3, и в этом случае/ = 0.Это означает, что все переменные являются фиксированными (тройные точки в системе, например, см. Рисунок 11 или 14).
2.Пример. Равновесие системы с 1 степенью свободы (одномерное равновесие).Жидкость, находящаяся в равновесии с насыщенным паром (§ 2), является примером системы с 1 степенью свободы. Или одномерный system.In в этом случае есть 2 фазы с 1 компонентом. / = — {«2-р -.(6.71)) Из уравнения (6.71) следует, что для общей мономиальной системы число фаз превышает число компонентов на единицу.Подобный этому п-с — \ — И.(6.72)
Таким образом, можно вывести отношение типа P = P (T), но только в виде производной. Каждая фаза имеет общее соотношение ЗН ^ ДФ ^ Ы ^ ДТ + в ^ ДП,я 1 Р = 1,2 ….. ы, ы + 1.(6.73) Если температура и давление изменяются вдоль кривой фазового равновесия T — > T — * — dT, то снова § 2, как и в пункте 1, они должны иметь д \ ТП = Д \ С, если = … = < / q</»、/ = 1、2 ….. С. (6.74)
Таким образом, из уравнений(6.73)и(6.74), -\ — 2 дифференциал dP, dT,….. получаем уравнение r + 1 для d \ ic.Вы можете написать их В (р) {р д \ іх-а / ИК)д И2 -. \ ДП-Н ..- Н {?DT=: сэр) dT、 r = 1, 2,…, с, с + 1. (6.75) (6.76) решение этой системы уравнений в dPjdT дает уравнение Клапейрона в качестве обобщения. З(я)н <л)… Н? • ДП• * £(<1 м)ДТ(П + 1) ф ^ ДГ(Т + 1) ДТ-и «Н \ В… Очевидно, что фактические расчеты требуют большого количества экспериментальных данных.Например, если рассматривать смесь KN03 и H20, то эта система относительно проста, так как KN03 не образует твердых гидратов и не смешивается при любой концентрации с водой в жидкой фазе. Количество ингредиентов c = 22), а именно KN03 и H20.Максимальное количество фаз в этом случае равно 4.Рассмотрим твердый KN03, насыщенный водный раствор и моновариетальное равновесие 3 фаз пара.
Состав определяют по 2-6 молярным фракциям в каждой phase.As вы знаете, рассмотрение значительно упрощается из-за того, что твердая фаза является чистым веществом KN03.Поэтому на данном этапе、 С другой стороны, в газовой фазе присутствием KN03 можно пренебречь для увеличения степени приближения. Поэтому только молярная доля KN03 в жидкой фазе остается композиционным параметром. * й>,= * ’ Х™О = 1-(6.79) (6.44), (6.57) и (6.77)-(6.79) в уравнение (6.76)、 ДП (1 — ($£>- ^n » pK)*(SKNOa ~~ 5KN03) xg gQx Он (\Р»жидкость\ жидкость ТВ \ * ^ ’ dl(1-x) — fH20 J — *(vKN03-t> KN0J 1) эта система рассматривалась в работах Мори [19]. 2) йод со значением с всегда следует понимать как минимальное значение Количество компонентов, которые должны быть указаны для определения конфигурации системы.Например, наличие 2-х компонентов Ионы K +и N03 ″ четко присутствуют в системе、 В том смысле, что это понятие фигурирует в правиле фазы, это означает, что система состоит из 2-х компонентов.
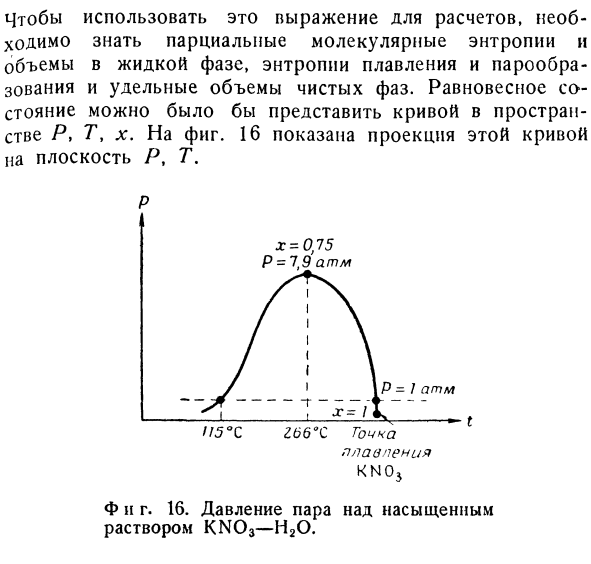
Эти ионы связаны со стехиометрическими условиями.Аналогично, гидрат KN03 (H20) I не является новым компонентом, но он может быть новой фазой. Чтобы использовать эту формулу для расчета, необходимо знать парциальную молекулярную энтропию и объем жидкой фазы, энтропию плавления и испарения, а также удельный объем чистой фазы.Равновесное состояние может быть представлено кривой в пространстве H, 7 \ lr.1 фиг. 図16は 、 曲線線の平面p この、T плоскостью Р кривой, tへの 投影 投影を示している。 П. С. Плавание. КМ5. F и d 16. Уравнение(6.80) может объяснить некоторые особенности этой кривой без какой-либо подробной информации.
Давление пара над насыщенным раствором KN03-H20. Людмила Фирмаль
Если величина х, возникающая при низких температурах, невелика, то давление пара должно возрастать примерно так же, как и в чистой воде при повышении температуры (см.§ 2, п. 1). в этом случае первый член и о * квартира」 Логические соображения применимы и к жидкой фазе.Когда температура повышается, растворимость l; как числитель, так и знаменатель правой части уравнения (6.80) increases.At в какой-то момент молекулы disappear.So, приблизительно при T = 266°C, x = 0.75 появляется некоторый максимум, максимум которого равен P = 7.9 атм.
Начиная с этой точки, давление уменьшается по мере повышения температуры до Х = 19, когда весь объем H2O исчезает из жидкой фазы. Отличительной особенностью системы KN03-H20 является наличие 2-ой точки кипения.Когда расплавленная соль KN03, насыщенная водой, быстро охлаждается, она сначала сильно кипит, затем затвердевает.Такое поведение наблюдается во многих многокомпонентных системах.
Смотрите также:
| Соотношение Гиббса — Дюгема | Идеальные смеси |
| Парциальные молекулярные величины | Общие условия равновесия. устойчивость |

